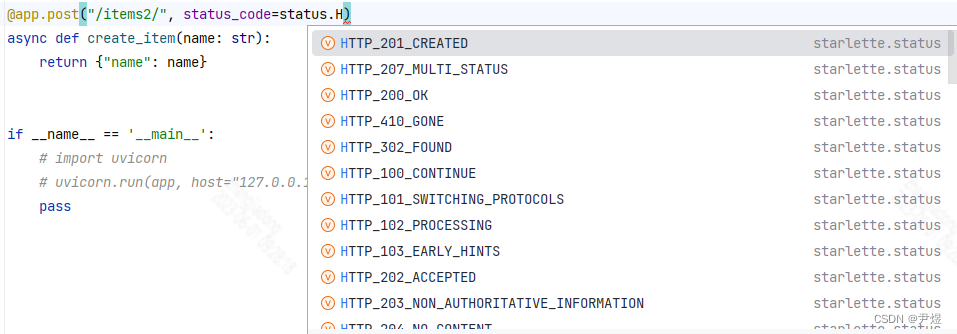
1. 传统DH参数方法
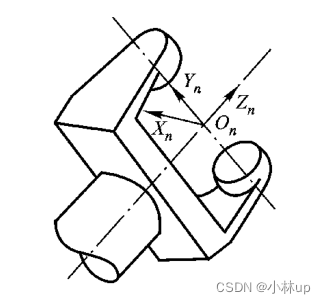
1.1 确定坐标系的方法
定义:杆 i i i的近端是关节 i i i,远端是关节 i + 1 i+1 i+1.
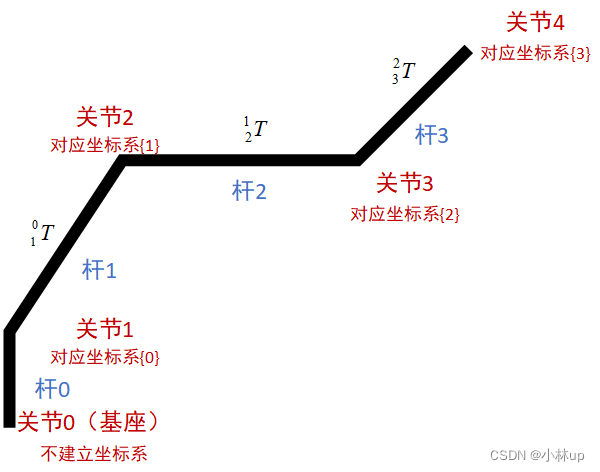
【下面的规则参考上面的图看得更清楚】
对于 n n n自由度机器人,可用以下步骤建立与各杆件 i ( i = 0 , 1 , … , n ) i(i=0,1,…,n) i(i=0,1,…,n)固连的坐标系 O i X i Y i Z i O_iX_iY_iZ_i OiXiYiZi,并简称其为系 i i i(注意:其中每一步都从 i = 0 i=0 i=0到 i = n i=n i=n进行完后再执行下一步骤)。
- 第1步:确定各坐标系的 Z Z Z轴。基本原则是:选取 Z i Z_i Zi轴沿关节 i + 1 i+1 i+1的轴向(指向可任选,但通常都将各平行的 Z Z Z轴均取为相同的指向)。这里需要说明的是:
当关节 i + 1 i+1 i+1是移动关节(即 σ i + 1 = 1 σ_{i+1}=1 σi+1=1)时,其轴线指向已知但位置不确定,这时选取 Z i Z_i Zi轴与 Z i + 1 Z_{i+1} Zi+1轴相交(若还有 σ i + 2 = 1 σ_{i+2}=1 σi+2=1,则取 Z i Z_i Zi轴和 Z i + 1 Z_{i+1} Zi+1轴都与 Z i + 2 Z_{i+2} Zi+2轴相交)
机器人杆 n n n的远端没有关节 n + 1 n+1 n+1,这时可选取 Z n Z_n Zn轴与 Z n − 1 Z_{n-1} Zn−1轴重合
- 第2步:确定各坐标系的原点 O O O。基本原则是:选取原点 O i O_i Oi在过 Z i − 1 Z_{i-1} Zi−1轴和 Z i Z_i Zi轴的公法线上(即 O i O_i Oi为此公法线与 Z i Z_i Zi轴的交点)。这里要说明的是:
当 Z i − 1 Z_{i-1} Zi−1轴与 Z i Z_i Zi轴平行时,经过两轴的公法线不唯一,确定 O i O_i Oi的方法是:若 Z i − 1 Z_{i-1} Zi−1轴与 Z i Z_i Zi轴重合,取 O i = O i − 1 O_i=O_{i-1} Oi=Oi−1·若 Z i − 1 Z_{i-1} Zi−1轴与 Z i Z_i Zi轴平行且不重合,过 O i − 1 O_{i-1} Oi−1点作 Z i − 1 Z_{i-1} Zi−1轴和 Z i Z_i Zi轴的公法线,取此公法线与 Z i Z_i Zi轴的交点为 O i O_i Oi.
由于没有 Z − 1 Z_{-1} Z−1轴,故无法按上述基本原则选取 O 0 O_0 O0。这时确定 O 0 O_0 O0的方法是:若 Z 0 Z_0 Z0与 Z 1 Z_1 Z1相交时,取 O 0 = O 1 O_0=O_1 O0=O1;若 Z 0 Z_0 Z0与 Z 1 Z_1 Z1不相交时,取 O 0 O_0 O0在 Z 0 Z_0 Z0与 Z 1 Z_1 Z1的公法线上。
- 第3步:确定各坐标系的 X X X轴。基本原则是:选取 X i X_i Xi轴沿过 Z i − 1 Z_{i-1} Zi−1轴和 Z i Z_i Zi轴的公法线,方向从 Z i − 1 Z_{i-1} Zi−1指向 Z i Z_i Zi.这里要说明的是:
当 Z i − 1 Z_{i-1} Zi−1轴与 Z i Z_i Zi轴重合时(这时 O i O_i Oi= O i − 1 O_{i-1} Oi−1),选取 X i X_i Xi轴满足在初始位置时 X i X_i Xi轴与 X i − 1 X_{i-1} Xi−1轴重合
当 Z i − 1 Z_{i-1} Zi−1轴与 Z i Z_i Zi轴相交且不重合时,选择 X i = ± ( Z i − 1 × Z i ) X_i=±(Z_{i-1}×Z_{i}) Xi=±(Zi−1×Zi),通常使所有平行的 X X X轴均有相同的指向。
当 i = 0 i=0 i=0时,由上所述知,这时 O 0 = O 1 O_0=O_1 O0=O1,或 O 0 O_0 O0在 Z 0 Z_0 Z0轴和 Z 1 Z_1 Z1轴的公法线上,选取在初始位置时 X 0 X_0 X0轴与 X 1 X_1 X1轴重合。
- 第4步:确定各坐标系的 Y Y Y轴。基本原则是使 Y i = Z i × X i Y_i=Z_i×X_i Yi=Zi×Xi,即构成右手坐标系。
1.2 DH参数的定义
当用 DH 方法建立起各杆件坐标系后, 系 i − 1 i-1 i−1 和系 i i i 间的相对位置和指向可用以下4 个参数表示:
(1)杆件长度 a i a_i ai , 定义为从 Z i − 1 Z_{i-1} Zi−1 轴到 Z i Z_i Zi 轴的距离, 沿 X i X_i Xi轴的指向为正.
(2)杆件扭角 α i \alpha_i αi, 定义为从 Z i − 1 Z_{i-1} Zi−1轴到 Z i Z_{i} Zi轴的转角, 绕 X i X_{i} Xi轴正向转动为正, 且规定 α i ∈ ( − π , π ] \alpha_{i}\in(-\pi, \pi] αi∈(−π,π] .
(3)关节距离 d i d_i di , 定义为从 X i − 1 X_{i-1} Xi−1 轴到 X i X_i Xi 轴的距离, 沿 Z i − 1 Z_{i-1} Zi−1 轴的指向为正。
(4)关节转角 θ i \theta_i θi,定义为从 X i − 1 X_{i-1} Xi−1 轴到 X i X_i Xi 轴的转角, 沿 Z i − 1 Z_{i-1} Zi−1 轴的指向为正,且规定 θ i ∈ ( − π , π ] \theta_i\in(-\pi, \pi] θi∈(−π,π] .
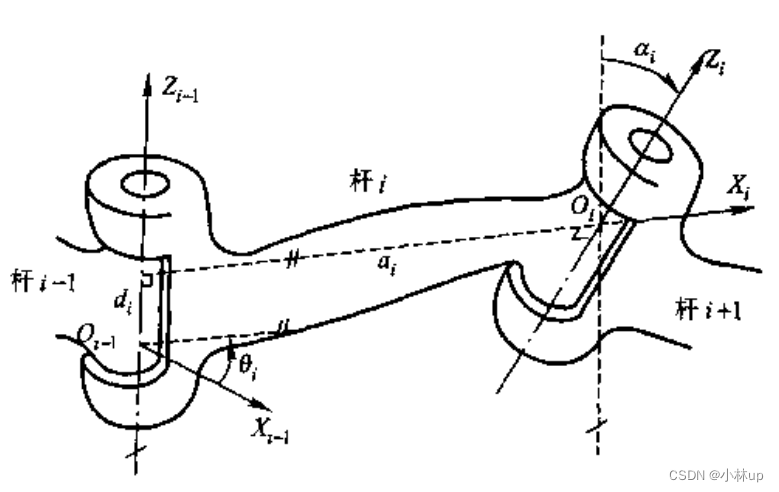
a i a_i ai和 α i \alpha_i αi由杆 i i i的结构确定,是常数;而 d i d_i di和 θ i \theta_i θi与关节 i i i的类型有关,其中一个是常数,另一个是变量.当关节 i i i是转动关节(即 σ i = 0 σ_i=0 σi=0)时, d i d_i di是常数, θ i \theta_i θi是变量;当关节 i i i是移动关节(即 σ i = 1 σ_i=1 σi=1)时, d i d_i di是变量, θ i \theta_i θi是常数.通常称 q i = ( 1 − σ i ) θ i + σ i d i q_i=(1-σ_i)\theta_{i}+σ_id_i qi=(1−σi)θi+σidi为关节变量, q i q_i qi刻画了系 i i i相对系 i − 1 i-1 i−1的运动
利用D-H参数的概念可看出,在用D-H方法建立杆坐标系时,如果某一步不能按基本原则唯一确定时,总是在设置时力图使更多的D-H参数为零(在后面的章节中可看出,这样做可以极大地简化机器人运动学与动力学模型及计算的复杂性).可不失一般性地认为一些D-H参数为零。可不失一般性地认为修改的D-H参数满足
a 1 = σ 1 θ 1 十 ( 1 − σ 1 ) d 1 = 0 a n = α n = σ n θ n 十 ( 1 − σ n ) d n = 0 a_1=\sigma_1\theta_1十(1-\sigma_1)d_1=0\\\ a_n=\alpha_n=\sigma_n\theta_n十(1-\sigma_n)d_n=0 a1=σ1θ1十(1−σ1)d1=0 an=αn=σnθn十(1−σn)dn=0
- 有时为应用方便,也可不像前面所述那样设置系,而是将系 n n n设置在机器人末端夹持器的端点,或在其所夹持工具的端点
1.3 DH参数齐次变换矩阵
最终效果:
-
第1步:沿 Z i − 1 Z_{i-1} Zi−1轴移动 d i d_i di
-
第2步:绕 Z i − 1 Z_{i-1} Zi−1轴转动 θ i \theta_i θi
-
第3步:沿 X i X_i Xi轴移动 a i a_i ai
-
第4步:绕 X i X_i Xi轴转动 α i \alpha_i αi
列写DH参数表时描述其连接的 i − 1 i-1 i−1坐标系和 i i i坐标系之间的关系。(i从1开始)
i
−
1
A
i
=
Trans
z
(
d
i
)
Rot
z
(
θ
i
)
Trans
x
(
a
i
)
Rot
x
(
α
i
)
=
[
cos
(
θ
i
)
−
sin
(
θ
i
)
cos
(
α
i
)
sin
(
θ
i
)
sin
(
α
i
)
a
i
cos
(
θ
i
)
sin
(
θ
i
)
cos
(
θ
i
)
cos
(
α
i
)
−
cos
(
θ
i
)
sin
(
α
i
)
a
i
sin
(
θ
i
)
0
sin
(
α
i
)
cos
(
α
i
)
d
i
0
0
0
1
]
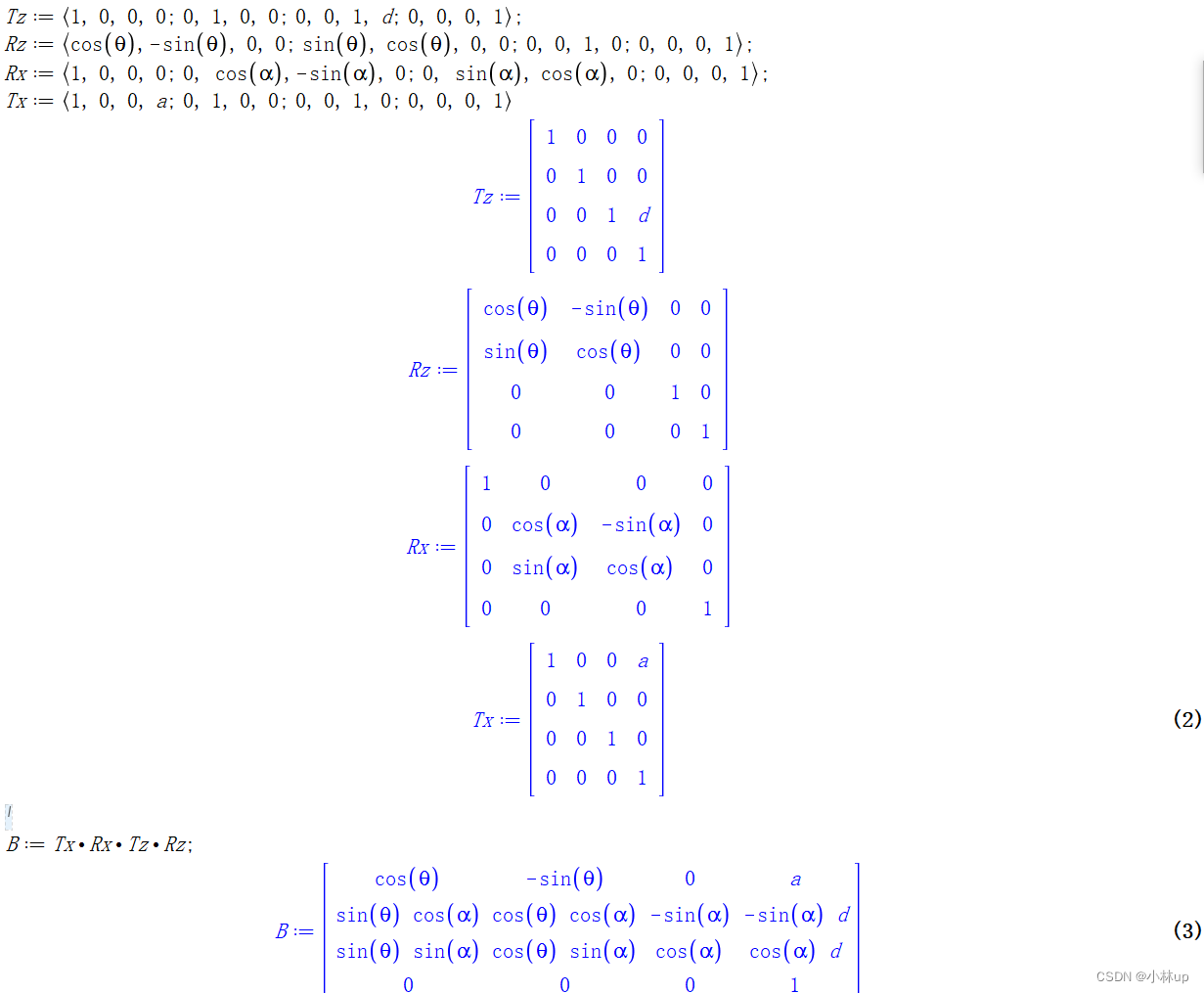
\begin{aligned} { }^{{i}-1} {~A}_{{i}} & =\operatorname{Trans}_{{z}}\left({d}_{{i}}\right) \operatorname{Rot}_{{z}}\left(\theta_{{i}}\right) \operatorname{Trans}_{{x}}\left({a}_{{i}}\right) \operatorname{Rot}_{{x}}\left(\alpha_{{i}}\right) \\ & =\left[\begin{array}{cccc} \cos (\theta_i) & -\sin (\theta_i) \cos (\alpha_i) & \sin (\theta_i) \sin (\alpha_i) & a_i\cos (\theta_i) & \\ \sin (\theta_i) & \cos (\theta_i) \cos (\alpha_i) & -\cos (\theta_i) \sin (\alpha_i) & a_i\sin (\theta_i) \\ 0 & \sin (\alpha_i) & \cos (\alpha_i) & d_i \\ 0 & 0 & 0 & 1 \end{array}\right] \end{aligned}
i−1 Ai=Transz(di)Rotz(θi)Transx(ai)Rotx(αi)=
cos(θi)sin(θi)00−sin(θi)cos(αi)cos(θi)cos(αi)sin(αi)0sin(θi)sin(αi)−cos(θi)sin(αi)cos(αi)0aicos(θi)aisin(θi)di1
用Maple简单计算了一下:
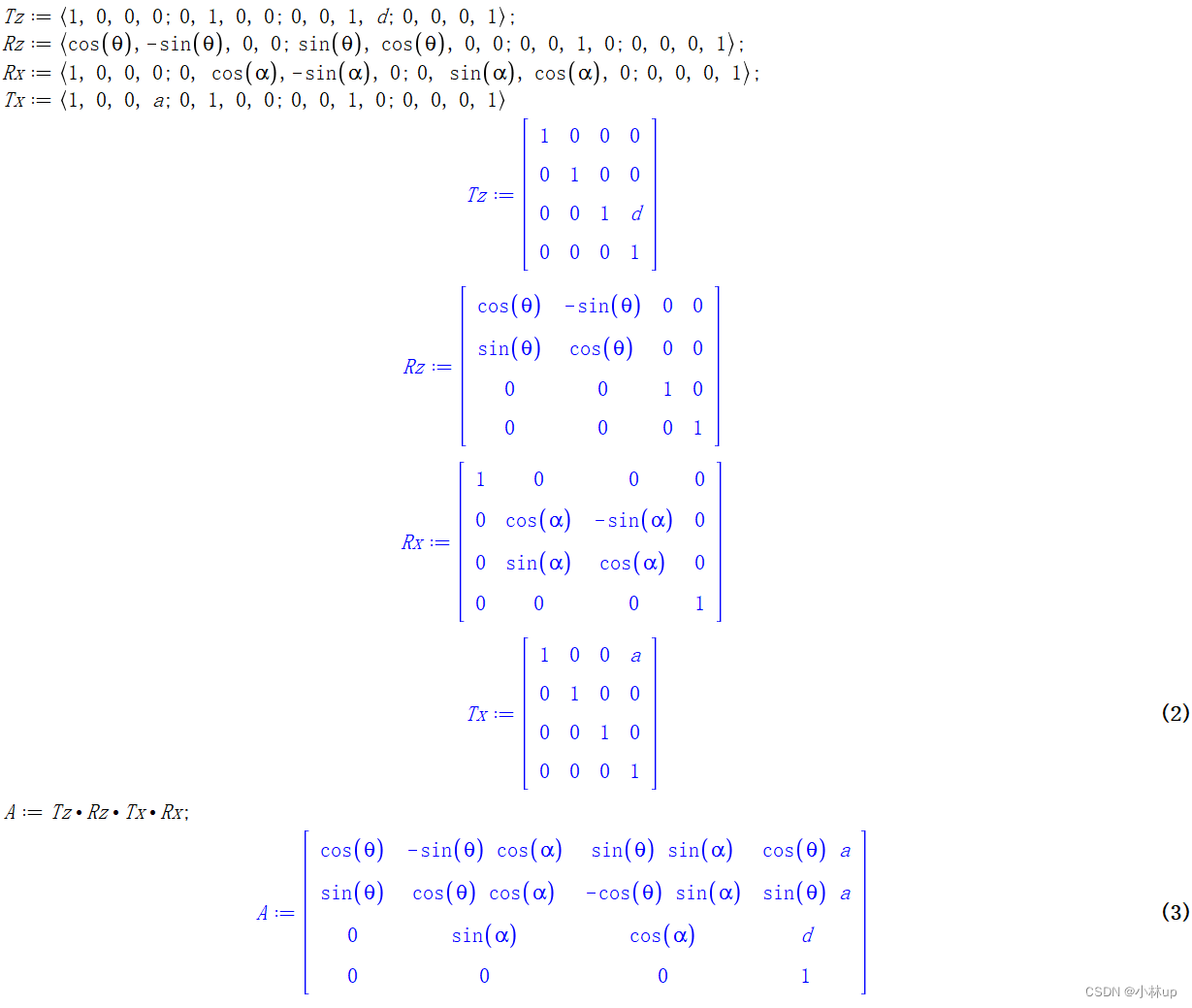
1.4 检验
可以试着做一下这个题目,加深一下理解:
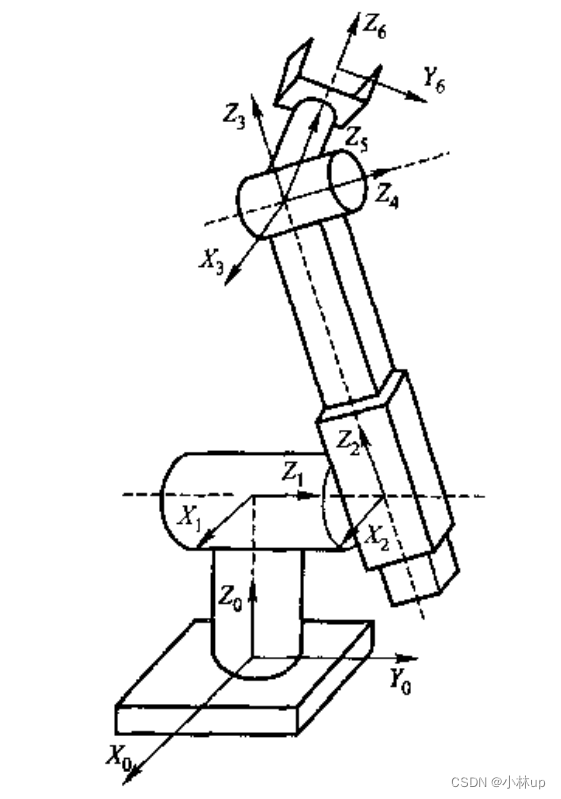
| i i i | a i a_i ai | α i \alpha_i αi | d i d_i di | θ i \theta_i θi |
|---|---|---|---|---|
| 1 | 0 | − π / 2 -\pi/2 −π/2 | d 1 d_1 d1 | θ 1 \theta_1 θ1(变量) |
| 2 | 0 | π / 2 \pi/2 π/2 | d 2 d_2 d2 | θ 2 \theta_2 θ2(变量) |
| 3 | 0 | 0 | d 3 d_3 d3(变量) | 0 |
| 4 | 0 | − π / 2 -\pi/2 −π/2 | 0 | θ 4 \theta_4 θ4(变量) |
| 5 | 0 | π / 2 \pi/2 π/2 | 0 | θ 5 \theta_5 θ5(变量) |
| 6 | 0 | 0 | d 6 d_6 d6 | θ 6 \theta_6 θ6(变量) |
2. 改进DH参数方法
杆 i i i的近端是关节 i i i,远端是关节 i + 1 i+1 i+1.驱动杆 i i i的力(或力矩)是经由关节 i i i的轴线施加到杆 i i i上的,故关节 i i i的轴称为杆 i i i的驱动轴(Driving Axis).对杆 i i i来说,关节 i + 1 i+1 i+1的作用是将杆i的运动和力传到杆 i + 1 i+1 i+1上,故关节 i + 1 i+1 i+1的轴称为杆 i i i的传动轴(Transmitting Axis),在用D-H方法建立杆坐标系时,和杆 i i i固连的坐标系 i i i的 Z Z Z轴沿杆 i i i的传动轴轴向,
于是很自然想到传统建立DH参数坐标系方法的一个明显缺点是:对于树形结构或含闭链的机器人,有的杆上会存在多于一个传动轴,这时用D一H方法建立杆坐标系时会产生歧义。
2.1 确定坐标系的方法
-
第1步:确定 Z i Z_i Zi轴。基本原则是: Z i Z_i Zi轴沿关节 i i i的轴向
-
第2步:确定原点 O i O_i Oi.基本原则是: O i O_i Oi在过 Z i Z_i Zi和 Z i + 1 Z_{i+1} Zi+1轴的公法线上。
-
第3步:确定 X i X_i Xi轴。基本原则是: X X X轴沿过 Z i Z_i Zi和 Z i + 1 Z_{i+1} Zi+1轴的公法线方向,从 Z i Z_i Zi指向 Z i + 1 Z_{i+1} Zi+1·
-
第4步:确定 Y i Y_i Yi轴。基本原则是: Y i = Z i × X i Y_i=Z_i\times X_i Yi=Zi×Xi,使坐标系为右手坐标系
2.2 DH参数的定义
①杆件长度 a i a_i ai,定义为从 Z i − 1 Z_{i-1} Zi−1到 Z i Z_i Zi的距离,沿 X i − 1 X_{i-1} Xi−1轴指向为正。
②杆件扭角 α i \alpha_i αi,定义为从 Z i − 1 Z_{i-1} Zi−1到 Z i Z_i Zi的转角。绕 X i − 1 X_{i-1} Xi−1轴正向转动为正。
③关节距离 d i d_i di,定义为从 X i − 1 X_{i-1} Xi−1到 X i X_i Xi的距离,沿 Z i Z_i Zi轴指向为正。
④关节转角 θ i \theta_i θi定义为从 X i − 1 X_{i-1} Xi−1到 X i X_i Xi的转角,绕 Z i Z_i Zi轴正向转动为正。
关于①和②也有《现代机器人学》的书这样描述(可能是现在主流的方法)*
①杆件长度 a i a_i ai,定义为从 Z i Z_{i} Zi到 Z i + 1 Z_{i+1} Zi+1的距离,沿 X i X_{i} Xi轴指向为正。
②杆件扭角 α i \alpha_i αi,定义为从 Z i Z_{i} Zi到 Z i + 1 Z_{i+1} Zi+1的转角。绕 X i X_{i} Xi轴正向转动为正。
需要注意的有以下几点:
①在建立驱动轴坐标系遇到不可应用基本原则的特殊情况时,也总是要使修改的D-H参数尽可能为零.特别是,当 i = 1 i=1 i=1和 i = n i=n i=n时,可不失一般性地认为修改的D-H参数满足
a 1 = α 1 = σ 1 θ 1 十 ( 1 − σ 1 ) d 1 = σ n θ n 十 ( 1 − σ n ) d n = 0 a_1=\alpha_1=\sigma_1\theta_1十(1-\sigma_1)d_1=\sigma_n\theta_n十(1-\sigma_n)d_n=0 a1=α1=σ1θ1十(1−σ1)d1=σnθn十(1−σn)dn=0
2.3 改进DH参数齐次变换矩阵
最终效果:
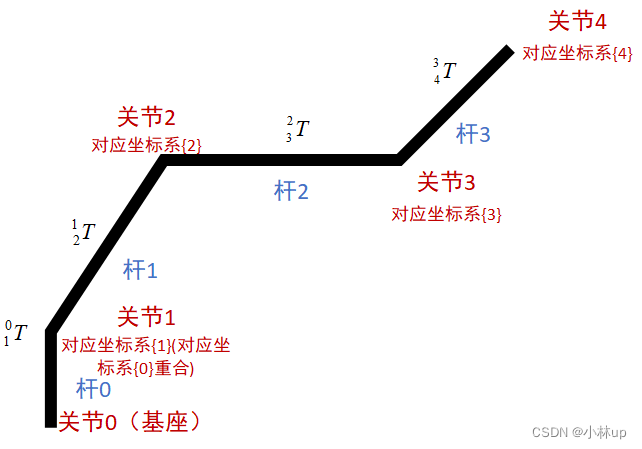
列写DH参数表时描述其连接的 i − 1 i-1 i−1坐标系和 i i i坐标系之间的关系。(i从1开始)
i − 1 A i = Trans x ( a i ) Rot x ( α i ) Trans z ( d i ) Rot z ( θ i ) = [ cos ( θ i ) − sin ( θ i ) 0 a i sin ( θ i ) cos ( α i ) cos ( θ i ) cos ( α i ) − sin ( α i ) − d i sin ( α i ) sin ( θ i ) sin ( α i ) cos ( θ i ) sin ( α i ) cos ( α i ) d i cos ( α i ) 0 0 0 1 ] \begin{aligned} { }^{{i}-1} {~A}_{{i}} & =\operatorname{Trans}_{{x}}\left({a}_{{i}}\right) \operatorname{Rot}_{{x}}\left(\alpha_{{i}}\right) \operatorname{Trans}_{{z}}\left({d}_{{i}}\right) \operatorname{Rot}_{{z}}\left(\theta_{{i}}\right) \\ & =\left[\begin{array}{cccc} \cos (\theta_i) & -\sin (\theta_i)& 0 & a_i \\ \sin (\theta_i)\cos(\alpha_i) & \cos (\theta_i) \cos (\alpha_i) & -\sin(\alpha_i) & -d_i\sin (\alpha_i) \\ \sin(\theta_i)\sin(\alpha_i) & \cos(\theta_i)\sin (\alpha_i) & \cos (\alpha_i) & d_i\cos(\alpha_i) \\ 0 & 0 & 0 & 1 \end{array}\right] \end{aligned} i−1 Ai=Transx(ai)Rotx(αi)Transz(di)Rotz(θi)= cos(θi)sin(θi)cos(αi)sin(θi)sin(αi)0−sin(θi)cos(θi)cos(αi)cos(θi)sin(αi)00−sin(αi)cos(αi)0ai−disin(αi)dicos(αi)1
如果按照《现代机器人学》的书对于 α \alpha α和 a a a的描述,齐次变换矩阵公式写作:
i − 1 A i = Trans x ( a i − 1 ) Rot x ( α i − 1 ) Trans z ( d i ) Rot z ( θ i ) = [ cos ( θ i ) − sin ( θ i ) 0 a i − 1 sin ( θ i ) cos ( α i − 1 ) cos ( θ i ) cos ( α i − 1 ) − sin ( α i − 1 ) − d i sin ( α i − 1 ) sin ( θ i ) sin ( α i − 1 ) cos ( θ i ) sin ( α i − 1 ) cos ( α i − 1 ) d i cos ( α i − 1 ) 0 0 0 1 ] \begin{aligned} { }^{{i}-1} {~A}_{{i}} & =\operatorname{Trans}_{{x}}\left({a}_{{i-1}}\right) \operatorname{Rot}_{{x}}\left(\alpha_{{i-1}}\right) \operatorname{Trans}_{{z}}\left({d}_{{i}}\right) \operatorname{Rot}_{{z}}\left(\theta_{{i}}\right) \\ & =\left[\begin{array}{cccc} \cos (\theta_i) & -\sin (\theta_i)& 0 & a_{i-1} \\ \sin (\theta_i)\cos(\alpha_{i-1}) & \cos (\theta_i) \cos (\alpha_{i-1}) & -\sin(\alpha_{i-1}) & -d_i\sin (\alpha_{i-1}) \\ \sin(\theta_i)\sin(\alpha_{i-1}) & \cos(\theta_i)\sin (\alpha_{i-1}) & \cos (\alpha_{i-1}) & d_i\cos(\alpha_{i-1}) \\ 0 & 0 & 0 & 1 \end{array}\right] \end{aligned} i−1 Ai=Transx(ai−1)Rotx(αi−1)Transz(di)Rotz(θi)= cos(θi)sin(θi)cos(αi−1)sin(θi)sin(αi−1)0−sin(θi)cos(θi)cos(αi−1)cos(θi)sin(αi−1)00−sin(αi−1)cos(αi−1)0ai−1−disin(αi−1)dicos(αi−1)1
2.4 检验
可以试着做一下传统DH方法那个题目,加深一下理解,自己重新建一下坐标系,写一下改进的DH参数
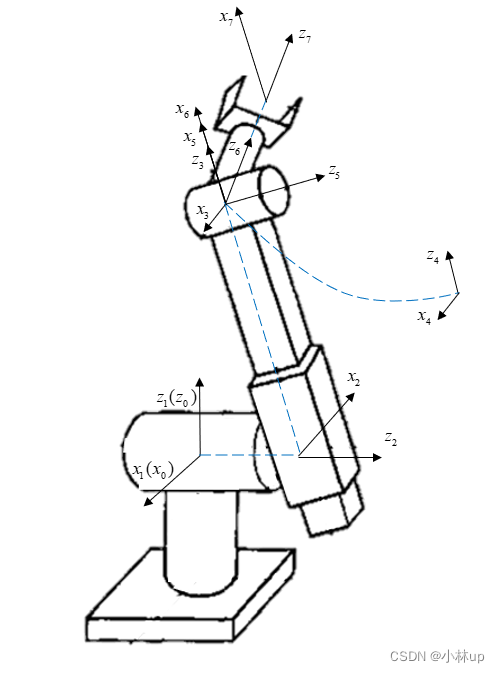
| i i i | a i a_i ai | α i \alpha_i αi | d i d_i di | θ i \theta_i θi |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | θ 1 \theta_1 θ1(变量) |
| 2 | 0 | − π / 2 -\pi/2 −π/2 | d 2 d_2 d2 | θ 2 \theta_2 θ2(变量) |
| 3 | 0 | − π / 2 -\pi/2 −π/2 | d 3 d_3 d3(变量) | π \pi π |
| 4 | 0 | 0 | 0 | θ 4 \theta_4 θ4(变量) |
| 5 | 0 | − π / 2 -\pi/2 −π/2 | 0 | θ 5 \theta_5 θ5(变量) |
| 6 | 0 | π / 2 \pi/2 π/2 | 0 | θ 6 \theta_6 θ6(变量) |
| 7 | 0 | 0 | d 6 d_6 d6 | 0 |
另外关于改进的DH方法可以看我的这篇博客
机器人学DH参数及利用matlab符号运算推导
写点自己的理解,如果有错误请大家指出,参考的是《机器人动力学与控制》这本书。