力扣动态规划专题（一）509 70 746 62 63 343 96 思路及C++实现

news2024/11/25 13:09:58

文章目录

  • 动态规划
  • 509. 斐波那契数
    • 五步骤
    • 代码
  • 70. 爬楼梯
    • 五步骤
    • 代码
  • 746. 使用最小花费爬楼梯
    • 五步骤
    • 代码
    • 扩展
  • 62. 不同路径
    • 动态规划
    • 数论
  • 63. 不同路径 II
    • 五步骤
    • 代码
  • 343. 整数拆分
    • 五步骤
    • 代码
  • 96.不同的二叉搜索树
    • 五步骤
    • 代码
  • 注意点：

动态规划

  1. 动态规划，DP，如果某一问题有很多重叠子问题，使用动态规划是最有效的。
  2. 与贪心的区别：动态规划中每一个状态一定是由上一个状态推导出来的；贪心没有状态推导，而是从局部直接选最优的。
  3. 动态规划五步骤：
  • 确定dp数组（dp table）以及下标的含义
  • 确定递推公式
  • dp数组如何初始化
  • 确定遍历顺序
  • 举例推导dp数组
  1. 动态规划题目

  • 基础：509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯、62.不同路径、63. 不同路径 II、343. 整数拆分、96.不同的二叉搜索树

  • 背包问题

    • 背包：416. 分割等和子集、1049.最后一块石头的重量II、494.目标和、474.一和零
    • 完全背包：518.零钱兑换II、377.组合总和Ⅳ、70爬楼梯、322.零钱兑换、279.完全平方数、139.单词拆分
    • 多重背包

  • 打家劫舍：198.打家劫舍、213.打家劫舍II、337.打家劫舍III

  • 股票问题：121. 买卖股票的最佳时机（只能买卖一次）、122.买卖股票的最佳时机II（可以买卖多次）、123.买卖股票的最佳时机III（最多买卖两次）、188.买卖股票的最佳时机IV（最多买卖k次）、309.最佳买卖股票时机含冷冻期（买卖多次，卖出一天有冷冻期）、714.买卖股票的最佳时机含手续费（买卖多次，每次有手续费）

  • 子序列问题

    • 不连续子序列：300.最长递增子序列、1143.最长公共子序列、1035.不相交的线
    • 连续子序列：674.最长连续递增子序列、718. 最长重复子数组、53. 最大子序和
    • 编辑距离：392.判断子序列、115.不同的子序列、583. 两个字符串的删除操作、72. 编辑距离
    • 回文：647. 回文子串、516.最长回文子序列

509. 斐波那契数

在这里插入图片描述

五步骤

  1. 确定dp数组以及下标的含义：题目给出了，斐波那契数F(n)就是dp数组，因此第i个数的斐波那契数值F(i)就是dp[i]

  2. 确定递推公式：题目给出了递推公式，F(n) = F(n - 1) + F(n - 2)，因此状态转移方程为dp[i] = dp[i - 1] + dp[i - 2]

  3. dp数组如何初始化：题目给出了初始值，F(0) = 0，F(1) = 1，因此dp[0] = 0，dp[1] = 1

  4. 确定遍历顺序：dp[i]是由dp[i - 1]和dp[i - 2]推导而来的，那么遍历顺序是从前往后

  5. 举例推导dp数组：假设i=7，那么dp数组应该是{0, 1, 1, 2, 3, 5, 8, 13}

代码

维护整个数组

class Solution {
public:
    int fib(int n) {
        if(n <= 1) return n;
        vector<int> dp(n+1);//创建dp数组
        dp[0] = 0;//dp数组初始值
        dp[1] = 1;//dp数组初始值
        //开始从前往后遍历
        for(int i=2; i<=n; i++)
        {
            dp[i] = dp[i-1] + dp[i-2];
        }
        return dp[n];
    }
};

改进，只维护两个数值

class Solution {
public:
    //改进，只维护两个数值，不是整个数组
    int fib(int n)
    {
        if(n <= 1) return n;
        int dp[2];//数组 仅维护两个数值
        dp[0] = 0;
        dp[1] = 1;
        int sum = 0;
        for(int i=2; i<=n; i++)
        {
            sum = dp[0] + dp[1];//中间状态记录
            dp[0] = dp[1];//当前dp[0] = 上一个dp[1]
            dp[1] = sum;//当前dp[1] = 上一个的 dp[0]+dp[1]
        }
        return dp[1];
    }
};

70. 爬楼梯

在这里插入图片描述

五步骤

  1. 确定dp数组以及下标的含义：dp[i]，爬到第i层楼梯，有dp[i]种方法

  2. 确定递推公式：
    题目中说每次可以爬1或2个台阶，那么有两个方向可以得到dp[i]
    如果只爬一个台阶，就从i-1层楼梯上一个台阶。即dp[i - 1]，上i-1层楼梯，有dp[i - 1]种方法，再上一个台阶就是dp[i]。
    如果只爬两个台阶，就从i-2层楼梯上两个台阶。即dp[i - 2]，上i-2层楼梯，有dp[i - 2]种方法，再上两个台阶就是dp[i]。
    所以dp[i]就是dp[i - 1]与dp[i - 2]之和，即dp[i] = dp[i - 1] + dp[i - 2]

  3. dp数组如何初始化：
    不考虑dp[0]如何初始化，只初始化dp[1] = 1，dp[2] = 2，然后从i = 3开始递推

  4. 确定遍历顺序：dp[i]是由dp[i - 1]和dp[i - 2]推导而来的，那么遍历顺序是从前往后

  5. 举例推导dp数组：假设i=10，那么dp数组应该是{1，2，3，5，8，13，21，44，65，109}

  6. 和斐波那契数唯一的区别就是没有dp[0]

代码

  • 维护整个数组
class Solution {
public:
    int climbStairs(int n) {
        //2.维护整个数组
        if(n <= 1) return n;
        vector<int> dp(n+1);
        dp[1] = 1;
        dp[2] = 2;
        for(int i=3; i<=n; i++)
        {
            dp[i] = dp[i-1] + dp[i-2];
        }
        return dp[n];
    }
};
  • 维护两个数值
class Solution {
public:
    int climbStairs(int n) {
        //1.只维护两个数值
        if(n <= 1) return n;
        int dp[3];
        dp[1] = 1;
        dp[2] = 2;
        int sum = 0;
        for(int i=3; i<=n; i++)
        {
            sum = dp[1] + dp[2];
            dp[1] = dp[2];
            dp[2] = sum;
        }
        return dp[2];
    }
};

746. 使用最小花费爬楼梯

五步骤

  1. 确定dp数组以及下标的含义：dp[i]，爬到第i层楼梯所花费最少的体力

  2. 确定递推公式：

  • 和70.爬楼梯相同的是，每次可以爬1或2个台阶，也就是有两个方向可以推导出dp[i]，即dp[i] = dp[i - 1] + dp[i - 2]。
  • 和70.爬楼梯不同的是，每次爬楼需要支付费用：
    从i-1层楼梯dp[i - 1] 再上 一个台阶到dp[i]，需要花费dp[i - 1] + cost[i - 1]
    从i-1层楼梯dp[i - 2] 再上 两个台阶到dp[i]，需要花费dp[i - 2] + cost[i - 2]
  • 因此到达dp[i]层楼梯，一共需要花费dp[i - 1] + cost[i - 1] + dp[i - 2] + cost[i - 2]。但题目中要求是最小花费，不是所有方法的总费用。到达dp[i]层楼梯，哪种方法下费用最少就用哪种方法爬楼，即dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])

  1. dp数组如何初始化：
    注意题目中描述的你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯，也就是说，到第0个或者第1个台阶不需要花钱，但是从第0个或者第1个台阶需要花钱，可以看题目给的例子。因此初始化dp[10] = 0，dp[1] = 0

  2. 确定遍历顺序：dp[i]是由dp[i - 1]和dp[i - 2]推导而来的，那么遍历顺序是从前往后

  3. 举例推导dp数组：假设使用题目的示例2，cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1]，则有

cost[i]1100111100111001
下标i0123456789
dp[i]0012233445

代码

  • 维护整个数组
class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        //1.维护整个数组
        vector<int> dp(cost.size()+1);
        dp[0] = 0;
        dp[1] = 0;
        for(int i=2; i<=cost.size(); i++)
        {
            dp[i] = min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2]);
        }
        return dp[cost.size()];
    }
};
  • 维护两个数值 使用数组
class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int dp[2];
        dp[0] = dp[1] = 0;
        int finalcost = 0;
        for(int i=2; i<=cost.size(); i++)
        {
            finalcost = min(dp[0]+cost[i-2], dp[1]+cost[i-1]);
            dp[0] = dp[1];
            dp[1] = finalcost;
        }
        return dp[1];
    }
};
  • 维护两个数值 不用数组
class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int dp0 = 0, dp1 = 0;
        int dpi;
        for(int i=2; i<=cost.size(); i++)
        {
            dpi = min(dp1+cost[i-1], dp0+cost[i-2]);
            dp0 = dp1;
            dp1 = dpi;
        }
        return dp1;
    }
};

扩展

如果按照第一步花钱，最后一步不花钱。也就是在第0个或者第1个台阶需要花钱，但是到达顶楼的时候不需要花钱

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        //4.如果按照 第一步是花钱的，最后一步不花钱
        vector<int> dp(cost.size()+1);
        dp[0] = cost[0];
        dp[1] = cost[1];
        for(int i = 2; i<cost.size(); i++)//顶楼不花钱 不取等号
        {
            dp[i] = min(dp[i-2], dp[i-1]) + cost[i];
        }
        //最后一步不花钱的话，取倒数第一步和倒数第二步的最小值
        return min(dp[cost.size()-1], dp[cost.size()-2]);
    }
};

62. 不同路径

在这里插入图片描述
在这里插入图片描述

动态规划

五步骤

  1. 确定dp数组以及下标的含义：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径

  2. 确定递推公式：和爬楼梯的题目类似，每次可以选择向下或者向右走，也就是有两个方向可以推导出dp[i][j]，即dp[i][j] = dp[i - 1][j] + dp[i][j-1]

  3. dp数组如何初始化：从(0, 0)的位置到(i, 0)的路径只有一条，所以dp[i][0]一定都是1，那么dp[0][j]也是1

  4. 确定遍历顺序：dp[i][j]是由dp[i - 1][j]和dp[i][j-1]推导而来的，也就是从上或者左边推导而来，那么遍历顺序是从左到右

  5. 举例推导dp数组：假设m=5，n=6，则有

111111
123456
136101521
1410203556
15153570126

代码

  • 两个数组，逐行逐列遍历，有m*n个位置，每个位置记录对应的路径数，保存每个位置的结果
111111
123456
136101521
1410203556
15153570126
class Solution {
public:
    int uniquePaths(int m, int n) {
        //1.两个数组
        vector<vector<int>> dp(m, vector<int>(n, 0));
        for(int i=0; i<m; i++) dp[i][0] = 1;//初始化
        for(int j=0; j<n; j++) dp[0][j] = 1;//初始化
        for(int i=1; i<m; i++)
        {
            for(int j=1; j<n; j++)
            {
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
};
  • 一个数组时，逐行遍历，只有n或m个位置，每个位置记录的是到达该位置的总路径数，数组只保存i=n的结果，每次都更新，滚动数组
i=1111111
i=2123456
i=3136101521
i=41410203556
i=515153570126
class Solution {
public:
    int uniquePaths(int m, int n) {
        //2.一个数组
        vector<int> dp(n, 0);
        for(int i=0; i<n; i++) dp[i] = 1;
        for(int j=1; j<m; j++)
        {
            for(int i=1; i<n; i++)
            {
                dp[i] += dp[i-1];
            }
        }
        return dp[n-1];
    }
};

数论

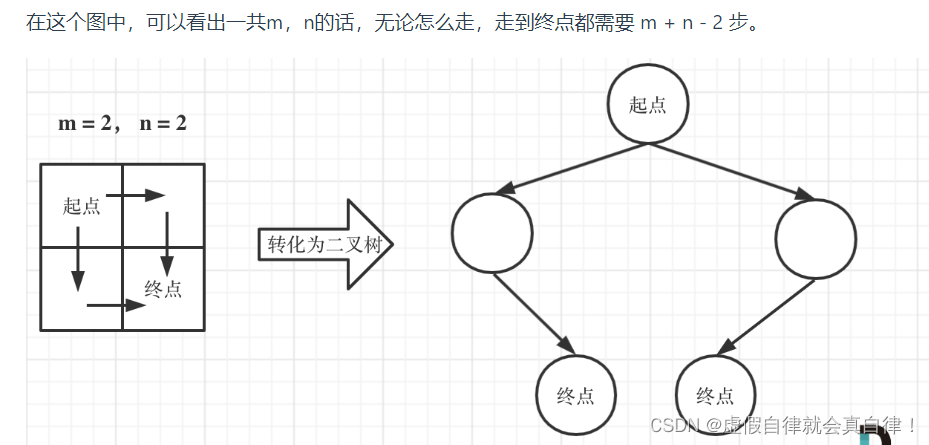
在这里插入图片描述
在这m + n - 2 步中，一定有 m - 1 步是要向下走的，不用管什么时候向下走。那么可以转化为组合问题，给m + n - 2个不同的数，随便取m - 1个数，有几种取法：

C m + n − 2 m − 1 C_{m+n-2}^{m-1} Cm+n−2m−1​ == C m − 1 + n − 1 m − 1 C_{m-1+n-1}^{m-1} Cm−1+n−1m−1​ == C m + n − 2 n − 1 C_{m+n-2}^{n-1} Cm+n−2n−1​ == ( m + n − 2 ) ! ( n − 1 ) ! × ( m − 1 ) ! {(m+n-2)!\over (n-1)!×(m-1)!} (n−1)!×(m−1)!(m+n−2)!​ == ( m − 1 + n − 2 ) × . . . × m × ( m − 1 ) × . . . × 2 × 1 ( n − 1 ) × . . . × 2 × 1 × ( m − 1 ) × . . . × 2 × 1 {(m-1+n-2)×...×m×(m-1)×...×2×1\over (n-1)×...×2×1×(m-1)×...×2×1} (n−1)×...×2×1×(m−1)×...×2×1(m−1+n−2)×...×m×(m−1)×...×2×1​ == ( m − 1 + n − 2 ) × . . . × m 1 {(m-1+n-2)×...×m\over 1} 1(m−1+n−2)×...×m​

注意最后结果是返回m×…×(m-1+n-2)，也就是分母除以分子的结果，还要注意分子溢出的情况，不能直接模拟公式计算。

class Solution {
public:
    int uniquePaths(int m, int n) {
        //3.数论 组合问题
        long long numerator = 1; // 分子
        int denominator = m - 1; // 分母
        int count = m-1;//相当于分子分母相消m-1项
        int t = m+n-2;//分子项
        while(count--)
        {
            numerator *= (t--);
            //分母不为0；numerator%denominator==0 表示找到相消项
            while(denominator!=0 && numerator%denominator==0)
            {
                numerator /= denominator;//更新结果
                denominator--;//分母项
            }
        }
        return numerator;
    }
};

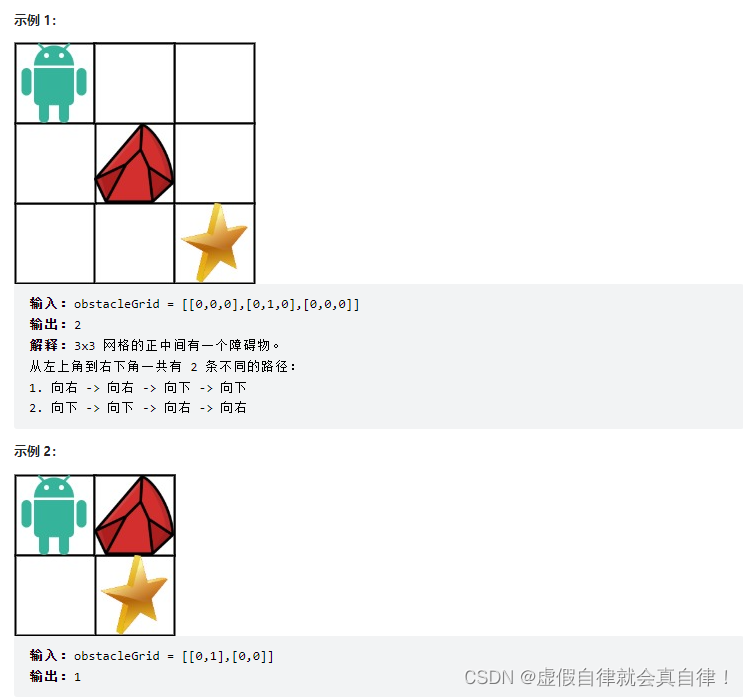
63. 不同路径 II

​在这里插入图片描述
在这里插入图片描述

五步骤

  1. 确定dp数组以及下标的含义：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径

  2. 确定递推公式：

  • 和62题一样，每次可以选择向下或者向右走，有两个方向可以推导出dp[i][j]，即dp[i][j] = dp[i - 1][j] + dp[i][j-1]
  • 和62题不一样的是，遇到障碍就保持初始状态，相当于重新出发
  1. dp数组如何初始化：
  • 从(0, 0)的位置到(i, 0)的路径只有一条，所以dp[i][0]一定都是1，那么dp[0][j]也是1
  • 如果(i, 0)位置有障碍，该位置及其后面的路都没有办法走，就要重新出发。即遇到障碍后，dp[i][0]=0，对于(0, j)的位置也是同样的处理
  1. 确定遍历顺序：dp[i][j]是由dp[i - 1][j]和dp[i][j-1]推导而来的，也就是从上或者左边推导而来，那么遍历顺序是从左到右
  2. 举例推导dp数组，略

代码

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        //1.动态数组 两个数组
        int n = obstacleGrid[0].size();
        int m = obstacleGrid.size();
        //起点或者终点有障碍物 无路可走
        if(obstacleGrid[0][0]==1 || obstacleGrid[m-1][n-1]==1) return 0;
        //初始化dp数组
        vector<vector<int>> dp(m, vector<int>(n, 0));
        for(int i=0; i<m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
        for(int j=0; j<n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;
        //更新dp数组
        for(int i=1; i<m; i++)
        {
            for(int j=1; j<n; j++)
            {
                if(obstacleGrid[i][j] == 1) continue;
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
};
  • 一个数组时，逐行遍历，只有n或m个位置，每个位置记录的是到达该位置的总路径数，数组只保存i=n的结果，每次都更新，滚动数组
class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        //2.动态数组 一个数组
        if(obstacleGrid[0][0] == 1) return 0;
        int n = obstacleGrid[0].size();
        vector<int> dp(n, 0);
        //初始化
        for(int j=0; j<n; j++)
        {
            if(obstacleGrid[0][j] == 1) dp[j] = 0;//遇到障碍物
            else if(j==0) dp[j] = 1;
            else dp[j] = dp[j-1];
        }
        //更新dp数组
        for(int i=1; i<obstacleGrid.size(); i++)
        {
            for(int j=0; j<n; j++)//注意这里从0开始
            {
                if(obstacleGrid[i][j] == 1) dp[j] = 0;
                else if(j!=0) dp[j] += dp[j-1];
            }
        }
        return dp[n-1];
    }
};

343. 整数拆分

在这里插入图片描述

五步骤

  1. 确定dp数组以及下标的含义：分拆数字i，可以得到的最大乘积为dp[i]

  2. 确定递推公式：

  • 有两个方向推导，j * (i - j)
  • j×(i - j)，直接把整数拆分为两个数相乘
  • j×dp[i - j]，相当于是拆分(i - j)，拆分成两个以及两个以上的个数相乘
  • 如果定义dp[i - j]×dp[j] 也是默认将一个数强制拆成4份以及4份以上了
  • 递推公式：dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j});，在递推公式推导的过程中，每次计算dp[i]，取最大值

  1. dp数组如何初始化：拆分0和拆分1的最大乘积没有意义。从dp[i]的定义来说，拆分数字2，得到的最大乘积是1，初始化dp[2] = 1。

  2. 确定遍历顺序：

  • dp[i]是由dp[i - 1]推导而来的，那么遍历顺序是从左到右
  • j的结束条件是 j < i - 1，也可以是 j < i，但是后者重复计算。j=1时，拆分j与i-1；j = i - 1时，拆分i-1与1，重复计算。
  • i从3开始，那么dp[i - j]=dp[2]，可以通过初始化值求出来

  1. 拆分一个数n使其乘积最大，那么一定是拆分成m个数值相近的因子相乘的乘积最大。10 拆成 3 * 3 * 4和拆成2 * 5，前者的乘积更大。虽然无法确定m，但m一定大于等于2，也就是意味着拆成两个相同的因子的乘积有可能是最大值。那么遍历j时，只需要遍历到 n/2 就可以了，但乘积一定不是最大值。

  2. 举例推导dp数组，n为10 时

i345678910
j1~21~31~41~51~61~71~81~9
i-j2~13~14~15~16~17~18~19~1
dp[i-j]dp[2]dp[3] dp[2]dp[4] dp[3] dp[2]dp[5] dp[4] dp[3] dp[2]dp[6] dp[5] dp[4] dp[3] dp[2]dp[7] dp[6] dp[5] dp[4] dp[3] dp[2]dp[8] dp[7] dp[6] dp[5] dp[4] dp[3] dp[2]dp[9] dp[8] dp[7] dp[6] dp[5] dp[4] dp[3] dp[2]
dp[i]dp[3]dp[4]dp[5]dp[6]dp[7]dp[8]dp[9]dp[10]

代码

class Solution {
public:
    int integerBreak(int n) {
    //1.动态规划
    vector<int> dp(n+1);
    dp[2] = 1;
    for(int i=3; i<=n; i++)//dp[1] dp[0]没有意义
    {
        //内层for循环有三种写法
        //1.for(int j=1; j<i; j++)
        //2.for(int j=1; j<i-1; j++)
        for(int j=1; j<=i/2; j++)
        {
            dp[i] = max(dp[i], max(j*(i-j), j*dp[i-j]));
        }
    }
    return dp[n];
    }
};

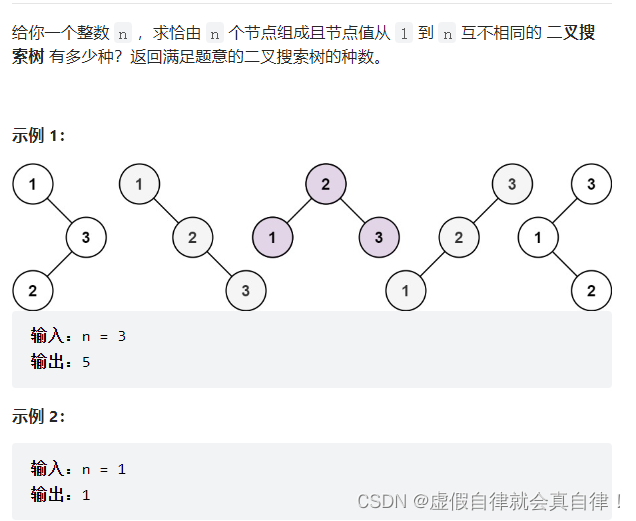
96.不同的二叉搜索树

在这里插入图片描述

五步骤

  1. 确定dp数组以及下标的含义：1到i为节点组成的二叉搜索树的个数为dp[i]，i个不同元素节点组成的二叉搜索树的个数

  2. 确定递推公式：
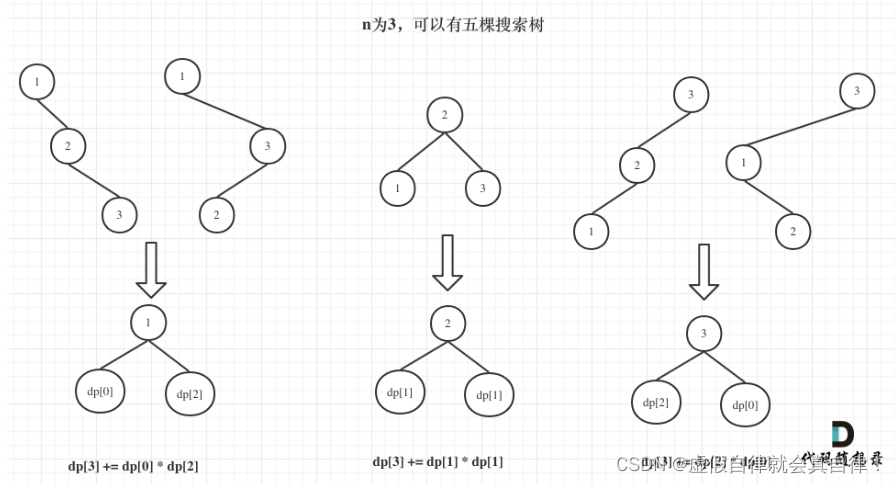
    在这里插入图片描述

  • 1为头结点时，相当于n=2的两棵树加了值为1的头结点，3为头结点时，亦同理。2为头结点时，布局同n=1的树。

  • dp[3]可以通过dp[1] 和 dp[2] 推导，即元素1为头结点搜索树的数量 + 元 素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量：

    • 元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量，dp[2] * dp[0]；
    • 元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量，dp[1] * dp[1]；
    • 元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量，dp[0] * dp[2]；

  • dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]

  • dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]，j相当于是头结点的元素，从1遍历到i为止。

  • dp[i] += dp[j - 1] * dp[i - j]; ，j-1 为j为头结点左子树节点数量，i-j 为以j为头结点右子树节点数量

  1. dp数组如何初始化：空节点也是一棵二叉树，也是一棵二叉搜索树，为了避免乘法为0，初始化dp[0]=1。

  2. 确定遍历顺序：dp[i] += dp[j - 1] * dp[i - j]可以看出，节点数为i的状态是依靠 i之前节点数的状态，用j来遍历i中每一个数作为头结点的状态

  3. 拆分一个数n使其乘积最大，那么一定是拆分成m个数值相近的因子相乘的乘积最大。10 拆成 3 * 3 * 4和拆成2 * 5，前者的乘积更大。虽然无法确定m，但m一定大于等于2，也就是意味着拆成两个相同的因子的乘积有可能是最大值。那么遍历j时，只需要遍历到 n/2 就可以了，但乘积一定不是最大值。

  4. 举例推导dp数组
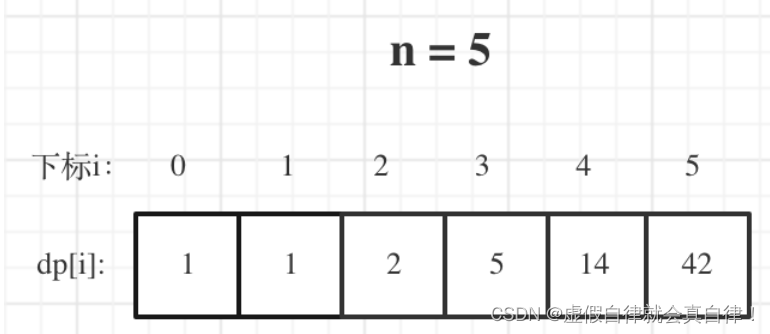
    在这里插入图片描述

代码

class Solution {
public:
    int numTrees(int n) {
        vector<int> dp(n+1);
        dp[0] = 1;//初始化空树的状态为1，避免乘法为0
        //更新dp数组
        for(int i=1; i<=n; i++)//以i为头结点的树
        {
            //符合条件的有多少棵树 用j从1-i遍历
            for(int j=1; j<=i; j++)
            {
                //对于第i个节点，需要考虑1作为根节点直到i作为根节点的情况，所以需要累加
                //一共i个节点，对于根节点j时,左子树的节点个数为j-1，右子树的节点个数为i-j
                //dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]
                dp[i] += dp[j-1] * dp[i-j];
            }
        }
        return dp[n];
    }
};

注意点：

  • 从509、70、746题来看，如果不到最后一层for循环的结束条件不取等号，到的话要取等号。例如，爬楼梯是，最后一层花钱或者要到顶楼的话，for循环的结束条件都要取等号。
  • 509、70、746题三个题大同小异，要注意dp数组初始化时要结合dp数组的定义，例如70、746题dp数组初始化的区别。
  • 不同路径可以用动态规划和数论的方法，数论注意分子溢出，注意遇到障碍物的处理方法
  • 不同的二叉搜索树，好难想到

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/599072.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Java多线程学习2

Java多线程学习2

1. 多线程 线程与任务的关系 脱离了任务的线程是没有意义的 线程对象是通过Thread类来创建的 任务是通过Runnable接口来定义的 1.继承Thread类 2.实现Runnable接口 3.实现Callable接口 &#xff08;与Runnable的区别&#xff0c;可以拿到返回值&#xff09; Thread线程…
阅读更多...
RK3588平台开发系列讲解（驱动基础篇）设备驱动 IO 控制

RK3588平台开发系列讲解（驱动基础篇）设备驱动 IO 控制

平台内核版本安卓版本RK3588Linux 5.10Android 12文章目录 沉淀、分享、成长，让自己和他人都能有所收获！😄 📢本篇我们来讲的 ioctl 接口。 在内核 3.0 以前，ioctl 接口的名字叫 ioctl;内核 3.0 以后，ioctl 接口的名字叫 unlocked_ioctl。unlocked_ioctl就是 ioctl 接…
阅读更多...
基于深度学习的高精度血小板检测识别系统（PyTorch+Pyside6+YOLOv5模型）

基于深度学习的高精度血小板检测识别系统（PyTorch+Pyside6+YOLOv5模型）

摘要&#xff1a;基于深度学习的高精度血小板检测&#xff08;红细胞RBC、白细胞WBC和血小板Platelet&#xff09;识别系统可用于日常生活中或野外来检测与定位血小板目标&#xff0c;利用深度学习算法可实现图片、视频、摄像头等方式的血小板目标检测识别&#xff0c;另外支持…
阅读更多...
程序设计综合实习(C语言):用指针优化学生成绩排名

程序设计综合实习(C语言):用指针优化学生成绩排名

一.目的 1&#xff0e;熟悉变量的指针和指向变量的的指针变量的概念和使用 2&#xff0e;熟悉数组的指针和指向数组的的指针变量的概念和使用 3. 掌握冒泡法或选择法排序的算法 4. 掌握函数的定义、调用、声明&#xff0c;以及参数的两种传递方式 二、实习环境 Visual Studio 2…
阅读更多...
模拟集成电路设计-MOS器件物理基础（模集系列持续更新）

模拟集成电路设计-MOS器件物理基础（模集系列持续更新）

学习目的 欠缺的学习路径&#xff1a; 固体物理&#xff0c;半导体器件物理&#xff0c;器件模型&#xff0c;电路设计。所有的半导体器件都看成一个黑盒子&#xff0c;只关注端电压电流。 最佳的学习路径&#xff1a;两手抓&#xff0c;因为有些二阶效应会影响到电路本身. 本…
阅读更多...
Vector-常用CAN工具 - 以太网工程更换环境无法打开解决

Vector-常用CAN工具 - 以太网工程更换环境无法打开解决

通常来说每个VN5000都有自己本身的以太网硬件网络配置&#xff0c;因此当我们打开别人的以太网CANoe工程或CANape工程的时候&#xff0c;无法进行正常的功能使用或者log的无法正常的显示&#xff0c;那我们该如何处理呢&#xff1f;这种情况常见的有以下2种可能&#xff1a; 1、…
阅读更多...
数据的表示与运算

数据的表示与运算

目录 一、进位计数制 二、信息编码 三、定点数数据表示 四、校验码 五、定点数补码加减运算 六、标志位的生成 七、定点数的移位运算 八、定点数的乘除运算 九、浮点数的表示 十、浮点数的运算 一、进位计数制 整数部分&#xff1a; 二进制、八进制、十六进制 --…
阅读更多...
机器人模型预测控制MPC（model predictive control）

机器人模型预测控制MPC（model predictive control）

当前控制动作是在每一个采样瞬间通过求解一个有限时域开环最优控制问题而获得。过程的当前状态作为最优控制问题的初始状态&#xff0c;解得的最优控制序列只实施第一个控制作用。这是它与那些使用预先计算控制律的算法的最大不同。本质上模型预测控制求解一个开环最优控制问题…
阅读更多...
使用APIPOST 进行压力测试

使用APIPOST 进行压力测试

使用APIPOST 进行压力测试 目录概述需求&#xff1a; 设计思路实现思路分析1.apipost 压力测试 参考资料和推荐阅读 Survive by day and develop by night. talk for import biz , show your perfect code,full busy&#xff0c;skip hardness,make a better result,wait for c…
阅读更多...
​【指针和数组区别与理解】超万字

​【指针和数组区别与理解】超万字

指针和数组的关系 指针指的是指针变量&#xff0c;不是数组&#xff0c;指针变量的大小是4/8个字节&#xff0c;是专门来存放地址的。数组也不是指针&#xff0c;数组是一块连续的空间&#xff0c;存放一组相同类型的数据的。 没有关系&#xff0c;但是它们之间有比较相似的地方…
阅读更多...
代理模式的学习与使用

代理模式的学习与使用

1、代理模式的学习 代理模式是一种结构型设计模式&#xff0c;它允许你提供一个代理对象&#xff0c;该对象可以控制对其他对象的访问。代理模式通过在代理对象和实际对象之间添加一个中间层&#xff0c;使得代理对象可以代表实际对象执行某些操作&#xff0c;从而实现对实际对…
阅读更多...
ARM-系统移植（开发环境搭建）

ARM-系统移植（开发环境搭建）

基于STM32MP157单片机 一、安装tftp服务器 首先保证ubuntu连接网络成功 1. 安装步骤 作用&#xff1a;完成ubuntu和开发板之间传输文件 1&#xff09;安装tftp服务器的安装包 sudo apt-get install tftpd-hpa tftp-hpa tftpd-hpa : 服务器端 tftp-hpa : 客户端 2&#x…
阅读更多...
Docker Desktop 如何运行容器

Docker Desktop 如何运行容器

第一次使用windows环境下的DockerDesktop记录下使用方法 1、配置镜像源&#xff0c;虽然配置了镜像源&#xff0c;但是在界面你还是搜索不到镜像&#xff0c;应该默认使用的是官方dockerhub的原因&#xff0c;后面可以手动创建避开这个问题。 2、运行系统的windows powershell…
阅读更多...
使用yolov5实现图像识别

使用yolov5实现图像识别

文章目录 开始之前下载依赖下载数据集标记数据集整理文件新建 yaml 文件开始训练模型选择训练完成使用模型进行识别自定义模型下载数据集下载地址分享问题 开始之前 你应当先克隆这个仓库 git clone https://github.com/ultralytics/yolov5 # clone下载完毕后&#xff0c;进入…
阅读更多...
【轻量化网络系列（5）】ShuffleNetV2论文超详细解读（翻译 ＋学习笔记+代码实现）

【轻量化网络系列（5）】ShuffleNetV2论文超详细解读（翻译 ＋学习笔记+代码实现）

前言 今天我们要讲的是ShuffleNetV2&#xff0c;它是由旷视科技团队在 2018 年提出的&#xff0c;原论文发表在ECCV上。在同等复杂度下&#xff0c;ShuffleNetV2比ShuffleNet和MobileNetv2更准确。这篇论文除了提出这个全新的轻量化网络结构以外&#xff0c;还创新性地提出四…
阅读更多...
redis第二章-第二课-主从模式和哨兵模式原理

redis第二章-第二课-主从模式和哨兵模式原理

主从模式 1、复制一份redis.conf&#xff0c;命名为redis-6380.conf文件 2、修改该文件&#xff0c;修改端口号&#xff0c;线程文件&#xff0c;日志文件&#xff0c;以及指定文件存放目录 3.在从节点上配置&#xff0c;这是核心配置 从本机6379的redis实例复制数据 replica…
阅读更多...
如何准备一场面试

如何准备一场面试

目录 一、心理准备1、内心的答案2、表述的答案 二、简历准备三、知识准备&面试流程1、一面&#xff1a;技术面2、二面&#xff1a;BOSS面3、终面&#xff1a;HR面 四、面试的技巧有哪些1、自信2、真诚3、主动4、复盘 五、补充&#xff1a;其他面试内容1、逻辑思维2、技术开…
阅读更多...
圆柱点云展开为平面点云

圆柱点云展开为平面点云

文章目录 简单计算图示目标&#xff1a;将圆柱点云展开为平面点云用途&#xff08;目前想到的&#xff09;思路&#xff1a;本文展开思路关键点 简单计算图示 目标&#xff1a;将圆柱点云展开为平面点云 注意&#xff1a;工业实际场景中只能获取可见区域的圆柱侧面&#xff0c…
阅读更多...
CC2530+ESP8266与手机APP通信

CC2530+ESP8266与手机APP通信

一、案例介绍 下面是一个基于CC2530和ESP8266的项目示例，演示了如何使用CC2530与ESP8266通信以及使用AT指令控制其WiFi模块设置和数据传输。 项目概述： 通过CC2530控制ESP8266将其配置成AP+TCP服务器模式，并通过手机APP连接到TCP服务器并完成数据传输。ESP8266将作为一个热…
阅读更多...
基于Nginx部署的LNMP及搭建论坛

基于Nginx部署的LNMP及搭建论坛

文章目录 1.部署LNMPLNMP架构拓扑图1.安装Nginx服务&#x1f60a;2.安装MySQL服务&#x1f923;3.安装配置PHP解析环境&#x1f602; 2.部署Discuz社区论坛Web应用3. 部署WordPress社区论坛Web应用4. fpm参数优化 1.部署LNMP LNMP架构拓扑图 1.安装Nginx服务&#x1f60a; ##…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023