1. 关于回归和多类分类
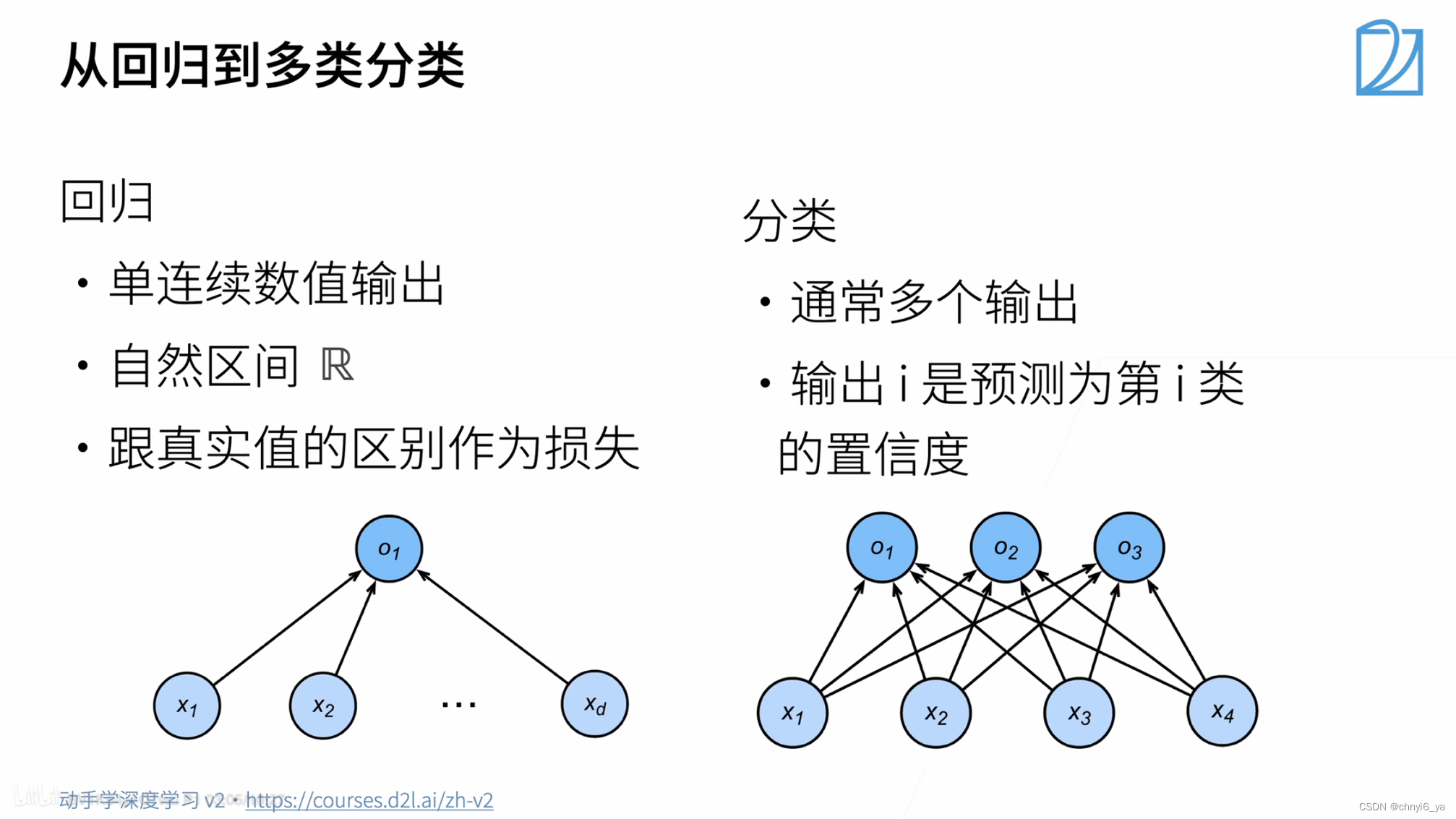
分类问题从回归的单输出变成了多输出,这个多输出的个数=类别的个数
置信度:置信度一词来自统计学,而统计学的本质是,用抽样的数据去估计整体的真实分布。例如,样本均值估计整体均值;还有,频率近似概率。而置信度的含义就是,你在用样本估计整体的时候,所得到的结论的“可信程度”,或者说,是对自己所的结论的一个量化的概率评价(打分)
2.从回归到多分类–均方损失
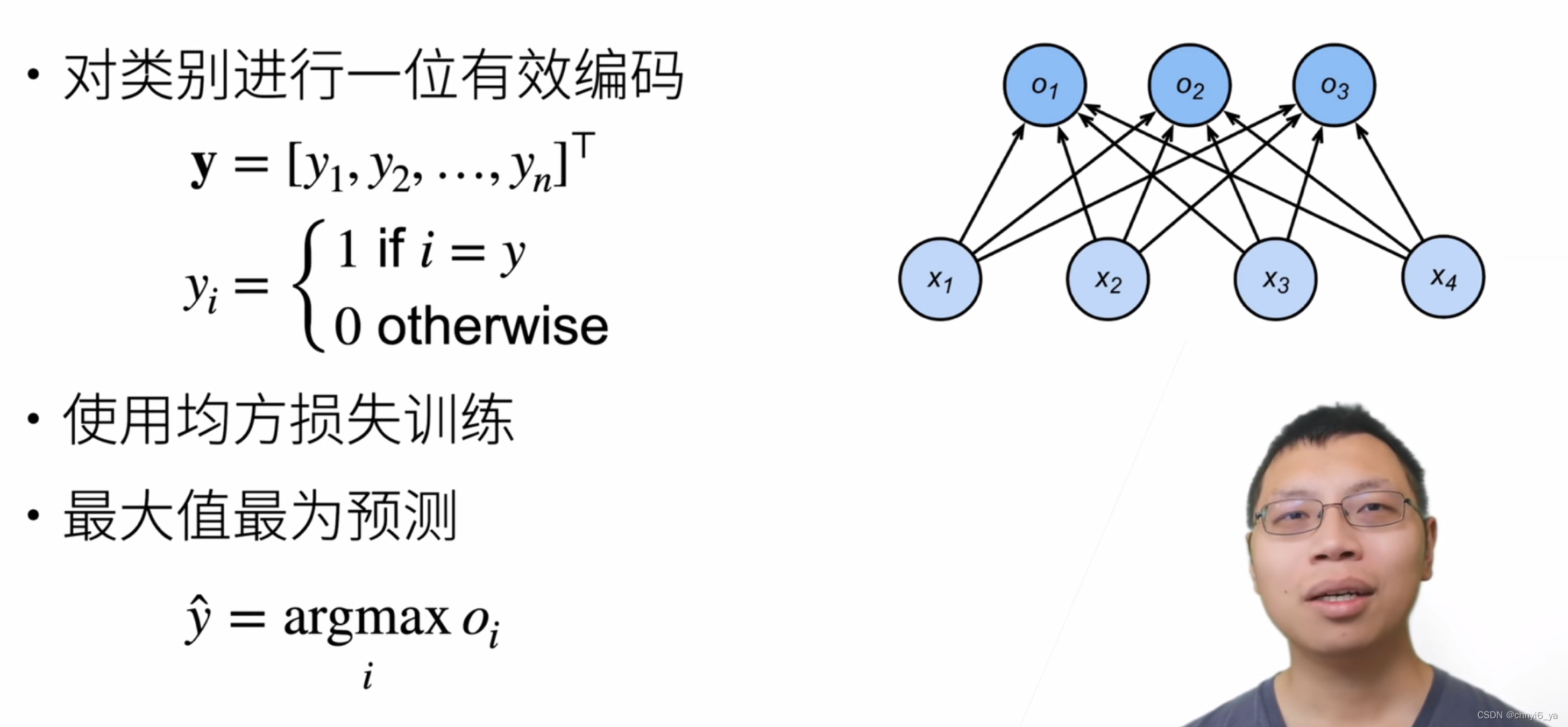
- 假设有n个类别,那么可以用最简单的一位有效编码来进行编码,标号就是一个长为n的向量。这个向量中,只有一个元素为1,对应的下标是第i个类别,其余元素为0。
- 如果训练出了一个模型,在做预测的时候,选取i使得最大化Oi的置信度的值作为预测,这个i就是预测的标号
3. 从回归到多类分类–无校验比例

正确类y的置信度oy要远远大于其他非正确类的oi,写成数学就是希望oy-oi要大于某一个阈值(oi是预测其他类的概率,oy是预测正确类的概率)
4. 从回归到多类分类–校验比例
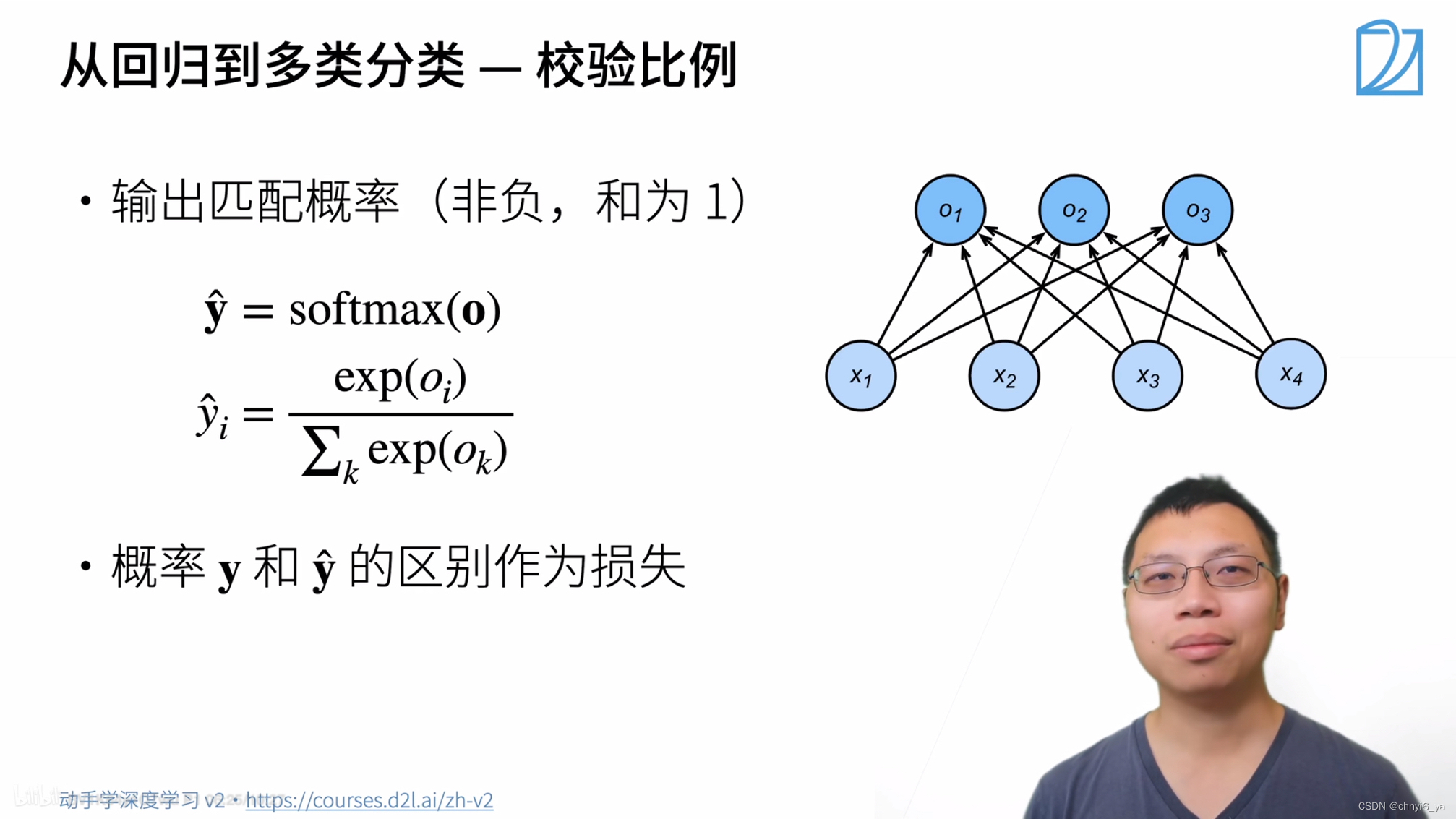
希望使得输出是一个概率,现在的输出是o1~on的向量,将softmax作用到o上看,得到一个长为n的向量y_hat,每个元素非负,且相加为1.
5. softmax 和 交叉熵损失

解释: 假设标签y将是一个三维向量, 其中(1,0,0)对应于“猫”、(0,1,0)对应于“鸡”、(0,0,1)对应于“狗”:
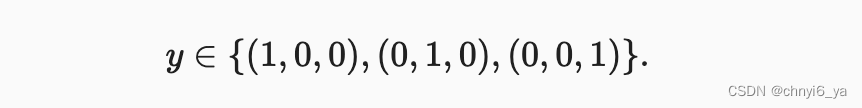
现在去预测一个样本,假设这个样本是鸡,也就是真实的概率是y=[0,1,0],而我们经过softmax预测之后得到的预测概率是y_hat= [0.1,0.8,0.1],那么:
损失函数l(y,y_hat) = -0* 0.1 - 1* 0.8 - 0* 0.1 = -1 * 0.8 , 得到的就是对于真实类别y预测得到的概率y_hat。因为真实样本向量中只有一个为1,其余为0,那么上图中的计算结果中的右下角的y就是表示,这个样本的真实类别y。
对于真实类别的预测值求log,再求负数,所以可以看出,对分类问题来讲,不关心对对于非正确类的预测值,我们只关心对于正确类的预测值,它的置信度要够大
下面对于如何得到梯度的过程进行展开:


最后,根据计算结果可以发现,梯度就等于预测概率和真实概率的差值。
6. 总结
- softmax回归是一个多类分类问题
- 使用softmax操作值得到每个类的预测置信度(概率,非负,和相加为1)
- 使用交叉熵来衡量预测和标号的区别(用交叉熵做损失函数)


![[Windows驱动开发] BlackBone介绍](https://img-blog.csdnimg.cn/fbe2db65fc394087a1cc14ad5664e687.png)


![[附源码]Python计算机毕业设计Django基于Java的员工管理系统](https://img-blog.csdnimg.cn/bb4f0c274f3348e289822f109cb78d53.png)