一、图的BFS

1、思路

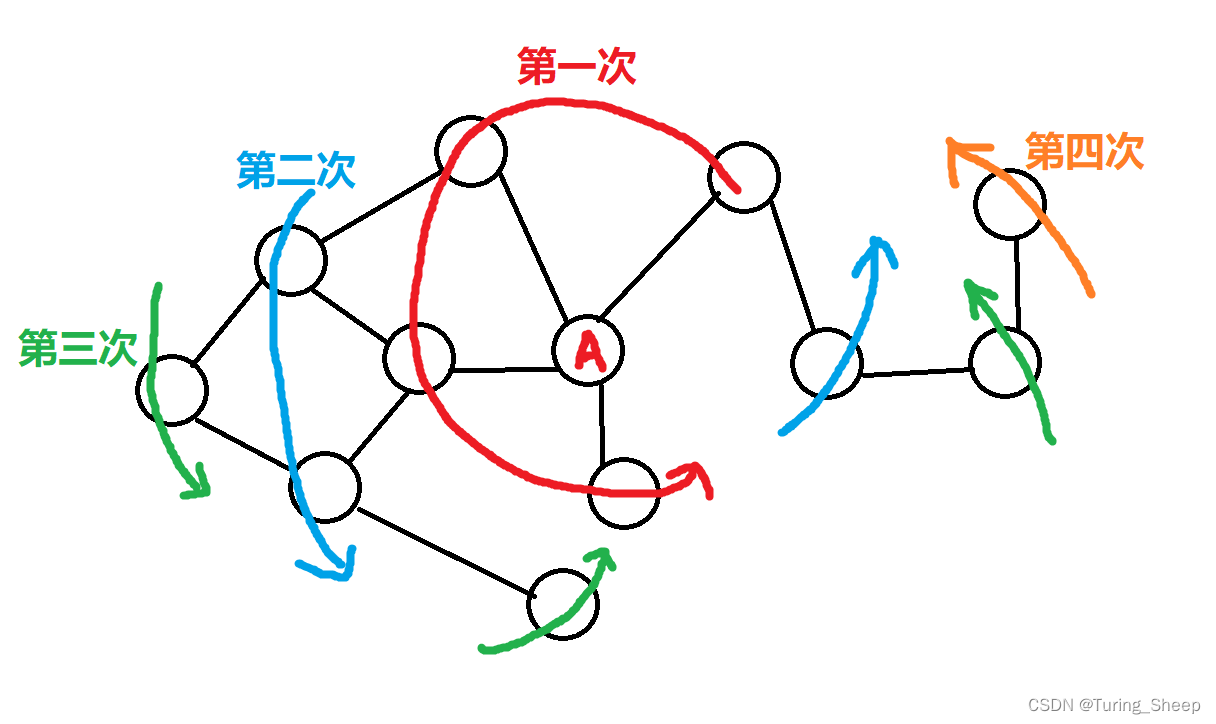
在这里插入图片描述
上图中的遍历顺序就是以A为起点开始的广度优先搜索。先遍历距离A点最近的距离，然后再依次向外拓展。

2、模板

（1）问题

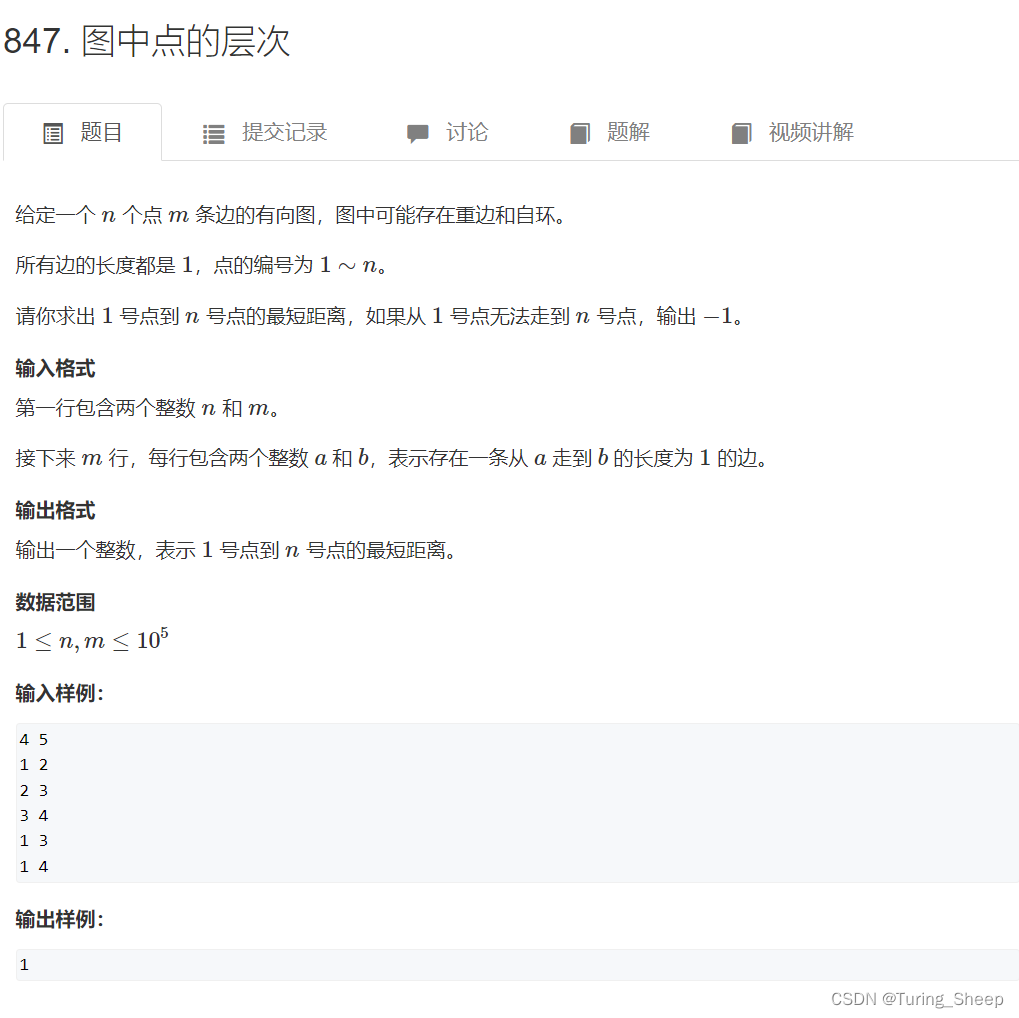
在这里插入图片描述
题目当中提到了最短路，同时每条边的权重都是1，同时在边权为1的情况下，我们的广度优先搜索是具备最短路的性质的。因此，我们采用BFS去做这道题。而最短路的证明，在前面讲解DFS和BFS的时候证明过，大家可以自行去看，这里附上链接：

同时，在该文章中，我还为大家介绍了，为什么BFS要用队列，如何保证搜到的是最短的等等常见问题：

DFS与BFS保姆级教学

（2）代码模板

#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
const int N=1e5+10;
const int M=3e5+10;
int h[N],e[M],ne[M],idx;
int m[N];
int n,k;
void add(int x,int y)
{
    e[idx]=y;
    ne[idx]=h[x];
    h[x]=idx++;
}
int bfs()
{
    queue<int>q;
    q.push(1);
    m[1]=0;
    while(!q.empty())
    {
        for(int i=h[q.front()];i!=-1;i=ne[i])
        {
            if(m[e[i]]==-1)
            {
                m[e[i]]=m[q.front()]+1;
                q.push(e[i]);
            }
            if(e[i]==n)goto A;
        }
        q.pop();
    }
    A:
    return m[n];
}
int main()
{
    memset(h,-1,sizeof h);
    memset(m,-1,sizeof m);
    cin>>n>>k;
    for(int i=0;i<k;i++)
    {
        int a,b;
        cin>>a>>b;
        add(a,b);
    }
    cout<<bfs();
    return 0;
}

（3）代码解析

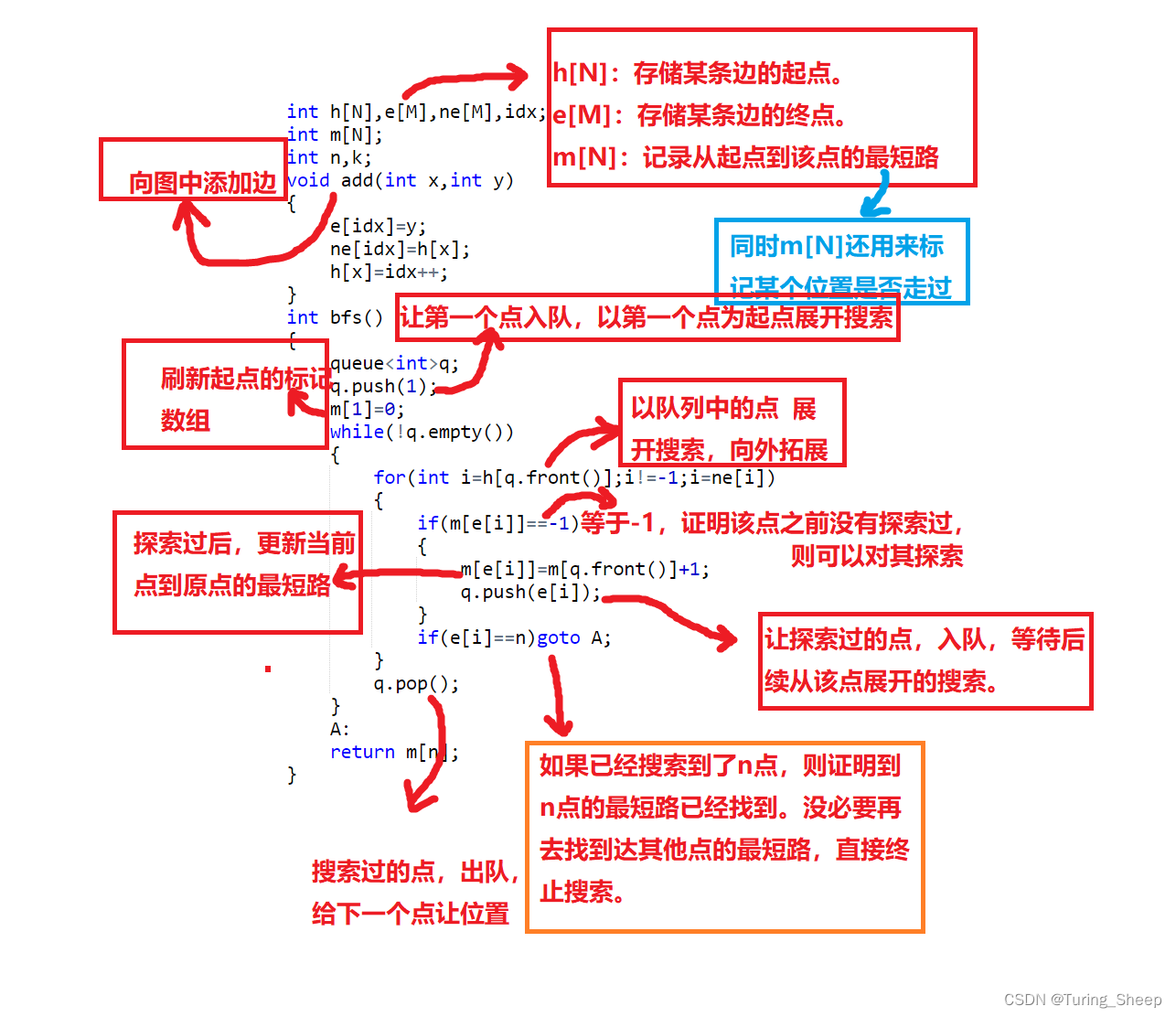
在这里插入图片描述

二、拓扑序列

引入：

在生活中，我们经常会遇到类似一下的场景。
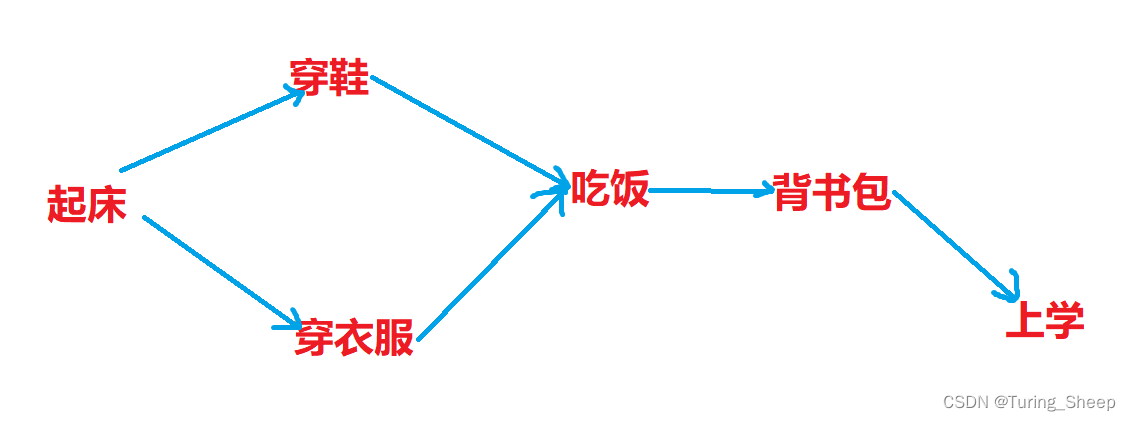
在这里插入图片描述
我们想要去上学的话，我们必须完成前面的一系列任务。不起床，怎么吃饭呢？不穿衣服，怎么上学呢？（当然，正常人的话）
那么我们有一下两条路可走：

起床–》穿鞋–》穿衣服–》吃饭–》背书包–》上学
起床–》穿衣服–》穿鞋–》吃饭–》背书包–》上学

这两条路都可以走，所以这两条路线都是正确的，这就是拓扑序列。

1、什么是拓扑序列？

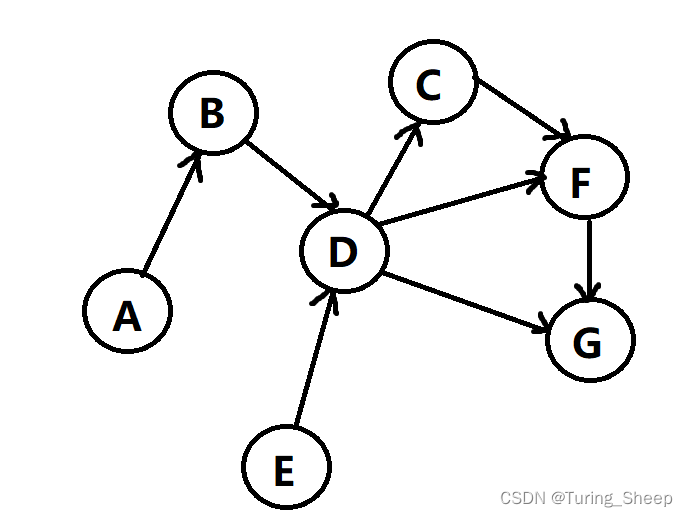
在这里插入图片描述
简单的说，拓扑序列就是有顺序地去访问图中的点。按照我们刚才的例子，我们发现，当一个点没有被指向的时候，这个点就相当于没有限制的，那么我们就可以直接访问，类似于A和E。那么被指向的路线个数称作：入度。从该点指出的路线个数叫做：出度。

比如：A点的入度为0,出度为1。D点的入度为2，出度为3。

所以，我们只有当某个点的入度是0的时候，才能够访问。

那么上图中，我们可以直接访问A和E，但是先访问谁都可以，因此拓扑序列并不唯一。例如上图中，我们可以写出一条可能的拓扑序列：

在这里插入图片描述

什么情况下没有拓扑序列呢？
我们看下面的情况;
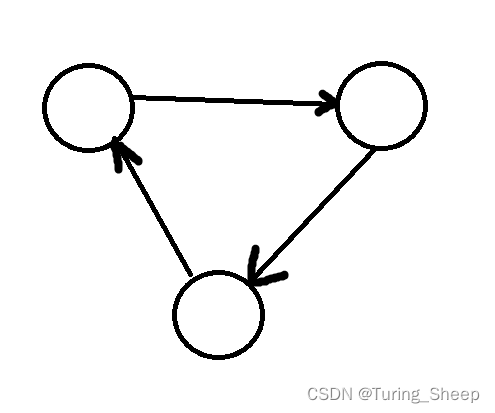
在这里插入图片描述
当一个图中出现这种环的时候，我们是无法写出拓扑序列的，因为图中没有度为0的点，因此我们无从下手。

2、模板：

（1）问题：

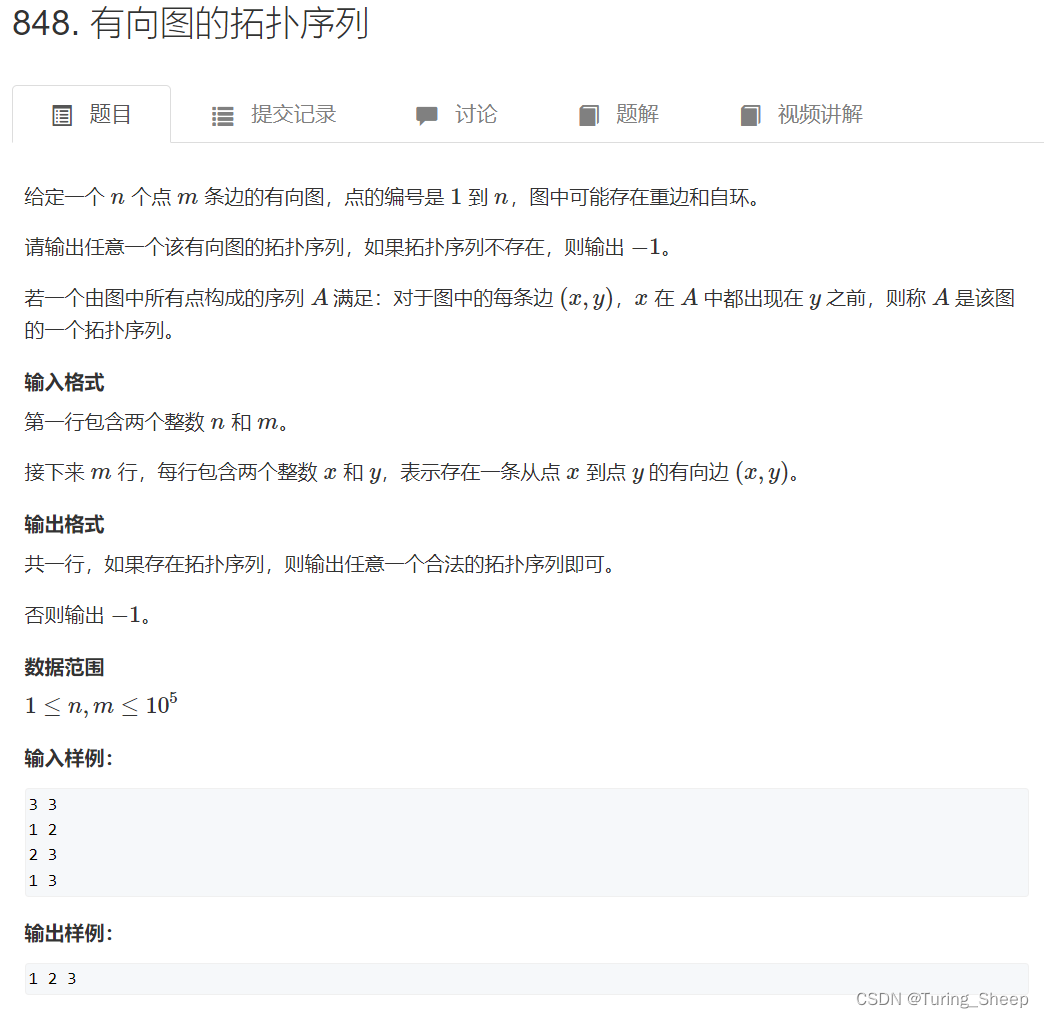
在这里插入图片描述
很明显，我们想要写出一个拓扑序列，就要从一个入度为0的点开始，当我们访问结束后，就可以删除这个点以及和这个点相关的边，然后再找下一个入度为0的点。即：逐个击破！

部分过程如下图所示：
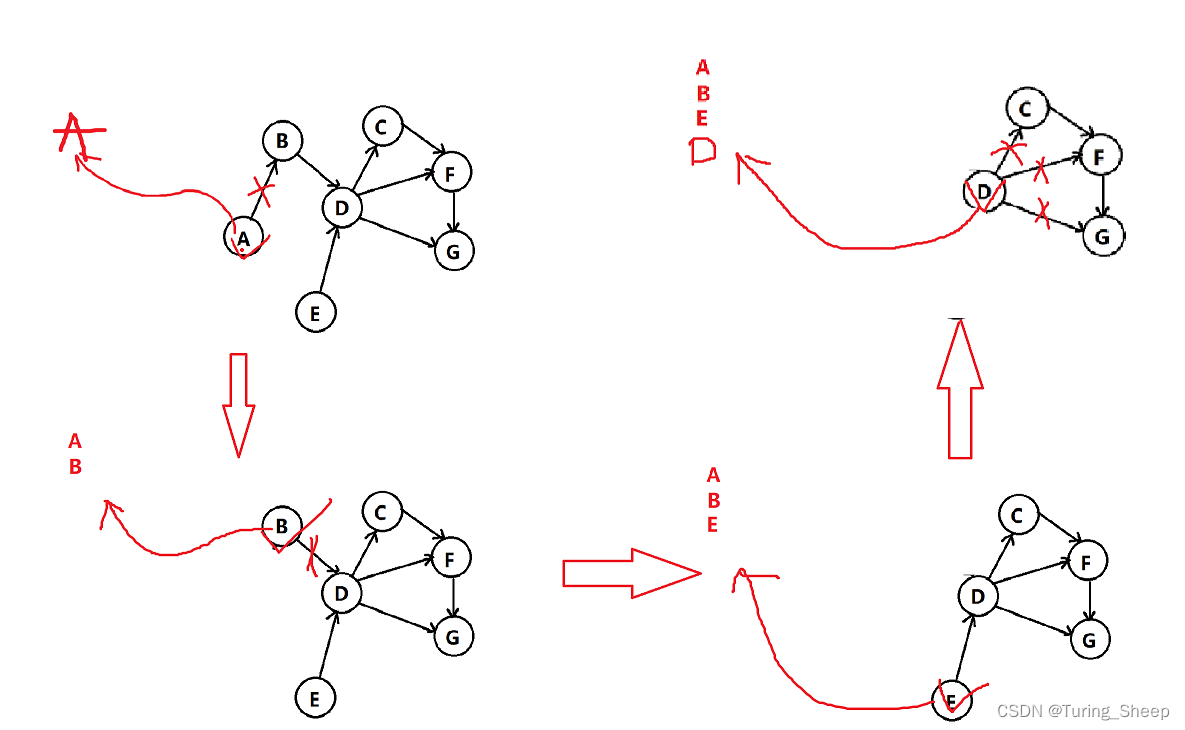
在这里插入图片描述
那么我们的思路就是先找到所有入度为0的点，然后通过BFS的逻辑，扫描该入度为零的点周围相连的点。为什么这样做呢？我们的目的就是通过BFS的扫描去删除该点所连的边。就如同上图中的D点。
我们通过D点，去扫描离他最近的CFG点，然后删除DC边，DF边，DG边。当删除以后，我们发现，C点从入度为1变成了入度为0，也就是说这个点可以访问了，那么我们让这个点进队。最后，我们发现这个队中的数据就是拓扑序列。具体的例子可以看图中左侧的红色字母序列。

（2）代码模板：

#include<iostream>
#include<cstring>
using namespace std;
const int N=1e5+10,M=3*N;
int h[N],e[M],ne[M],q[N],d[N],idx;
int n,m;
void add(int x,int y)
{
    e[idx]=y,ne[idx]=h[x],h[x]=idx++;
}
bool topsort()
{
    int hh=0,tt=-1;
    for(int i=1;i<=n;i++)if(!d[i])q[++tt]=i;
    while(hh<=tt)
    {
        int front=q[hh++];
        for(int i=h[front];i!=-1;i=ne[i])
        {
            if(--d[e[i]]==0)q[++tt]=e[i];
        }
    }
    int size=tt+1;
    return size==n;
}
int main()
{
    memset(h,-1,sizeof h);
    scanf("%d %d",&n,&m);
    for(int i=0;i<m;i++)
    {
        int x,y;
        scanf("%d %d",&x,&y);
        add(x,y),d[y]++;
    }
    if(!topsort())puts("-1");
    else
    {
        for(int i=0;i<n;i++)printf("%d ",q[i]);
    }
    
}