Compressed Bloom Filters论文总结

news2024/9/23 3:33:17

Compressed Bloom Filters论文总结

Abstract
I. INTRODUCTION
II. COMPRESSED BLOOM FILTERS:THEORY
- A. Bloom Filters
- B. Compressed Bloom Filters
III. COMPRESSED BLOOM FILTERS:PRACTICE
A. Examples
IV. DELTA COMPRESSION
V. COUNTING BLOOM FILTERS
VI. CONCLUSION

Abstract

我们引入了压缩Bloom Filters，当Bloom Filter作为消息传递时，它提高了性能，而它的传输大小是一个限制因素。

通过使用压缩Bloom过滤器，代理可以减少广播的比特数、假阳性概率和/或每次查找的计算量。代价是压缩和解压缩的处理时间，可以使用简单的算术编码，以及在代理处使用更多的内存，使用更大的未压缩形式的Bloom Filter。

I. INTRODUCTION

传输大小是正在发送的数据的大小；如果不使用压缩，它只是位数组的大小，但一旦引入压缩，它可能会更小。

通过使用压缩Bloom过滤器，协议减少了广播的比特数、假阳性概率和/或每次查找的计算量。

我们推荐算术编码，这是一种简单的压缩方案，非常适合这种情况，实现速度很快

可以通过在Bloom Filter中发送更改（或增量）而不是新的Bloom Filters来更新的情况。

II. COMPRESSED BLOOM FILTERS:THEORY

A. Bloom Filters

特定位仍然为0的概率为
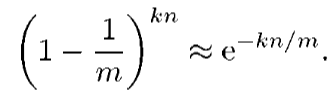
在这里插入图片描述

假阳性的概率是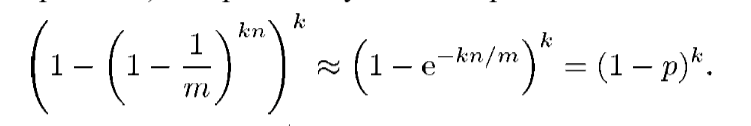在这里插入图片描述

B. Compressed Bloom Filters

我们可能不想为m和n优化哈希函数的数量，而是为需要发送的数据大小或传输大小优化哈希函数的数量。
然而，传输尺寸不必是m；我们也许可以压缩位数组。因此，我们选择我们的参数，使使用压缩后的失效概率最小。

假设Bloom Filter上的所有查找计算都是在代理处解压缩后完成的。
一个也提供随机访问的压缩方案可能允许我们在压缩的Bloom Filter上进行计算；然而，同时实现随机访问、效率和良好压缩通常是困难的。
一种可能是将Bloom Filter拆分为几个部分，并对每个部分进行压缩。查找一个位只需要解压缩筛选器的某一部分而不是整个筛选器，从而减少了所需的内存[11]。
如果在更新之间发生许多查找，这种方法将略微减少压缩，但会大大增加计算量。

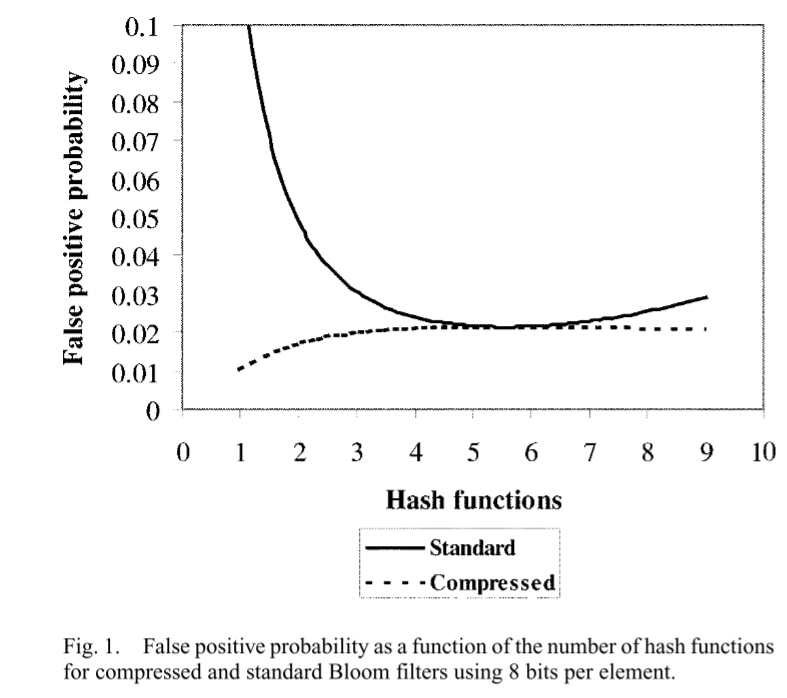
在没有压缩的情况下使假阳性概率最小的哈希函数的数量，实际上是在压缩的情况下使假阳性概率最大的哈希函数。

压缩的Bloom Filter使用更少的哈希函数，因此每次查找需要更少的计算量。

最好的压缩布卢姆过滤器实现了与标准布卢姆过滤器相同的假阳性概率，节省了大约30%的大小

压缩后的Bloom过滤器使用了更少数量的哈希函数，因此查找更有效。

III. COMPRESSED BLOOM FILTERS:PRACTICE

Restrictions on m:
压缩Bloom过滤器的大小z可能是首要的，但是对未压缩Bloom过滤器的大小的限制也限制了这种可能性
虽然理论上我们可以很好地使用一个哈希函数和压缩，但实现一个哈希函数的假阳性概率需要m≈n/ε，这对于实际应用来说可能太大了
Compression overhead:
压缩方案都有一些相关的开销，因此它们并不完全匹配熵公式所给出的空间
Compression variability:
压缩性能因输入而异。我们希望使我们的Bloom Filter内存大小尽可能大，同时保持压缩大小不超过给定阈值的高概率，这样我们就不会在几乎没有信息的情况下发送超过阈值的额外数据包。
如果不能预先确定集合中的元素数量，则错误的预测可能会产生不充分的压缩。
Hashing performance:
根据所选择的数据和哈希函数，实际哈希函数的行为可能与上面的分析不同。

选择所需的最大未压缩大小。然后利用上述理论设计了一个压缩bloom filter，其压缩尺寸比期望的要小一些
例如，如果目标是压缩大小为z，则设计结构以使压缩大小为0.99z。这为压缩中的一些可变性提供了空间。

每种过滤器类型都与大小数组、一组散列函数和一个解压缩方案相关联。