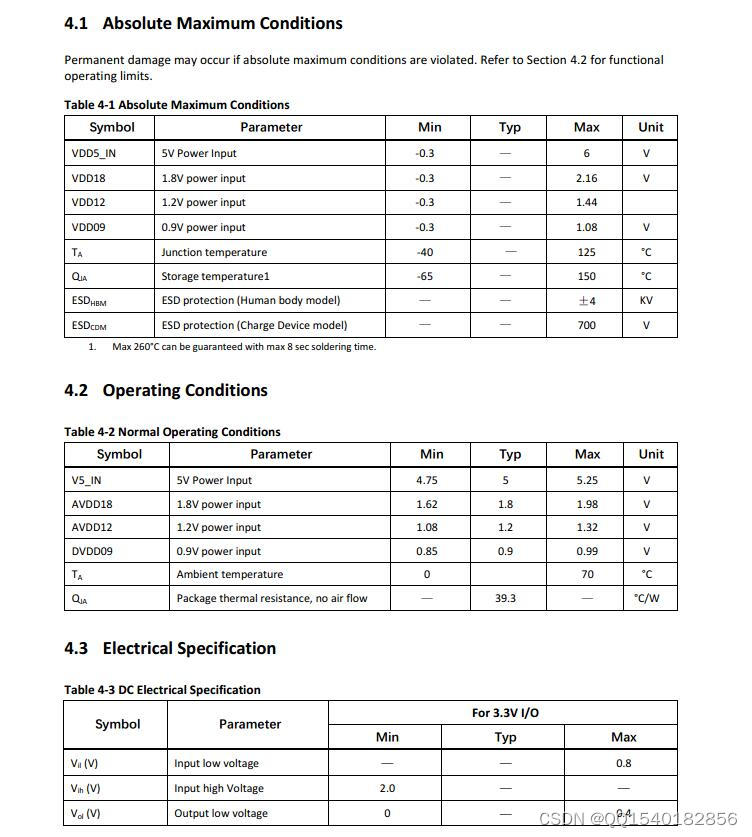
参考书目：《行为科学统计精要》（第八版）——弗雷德里克·J·格雷维特

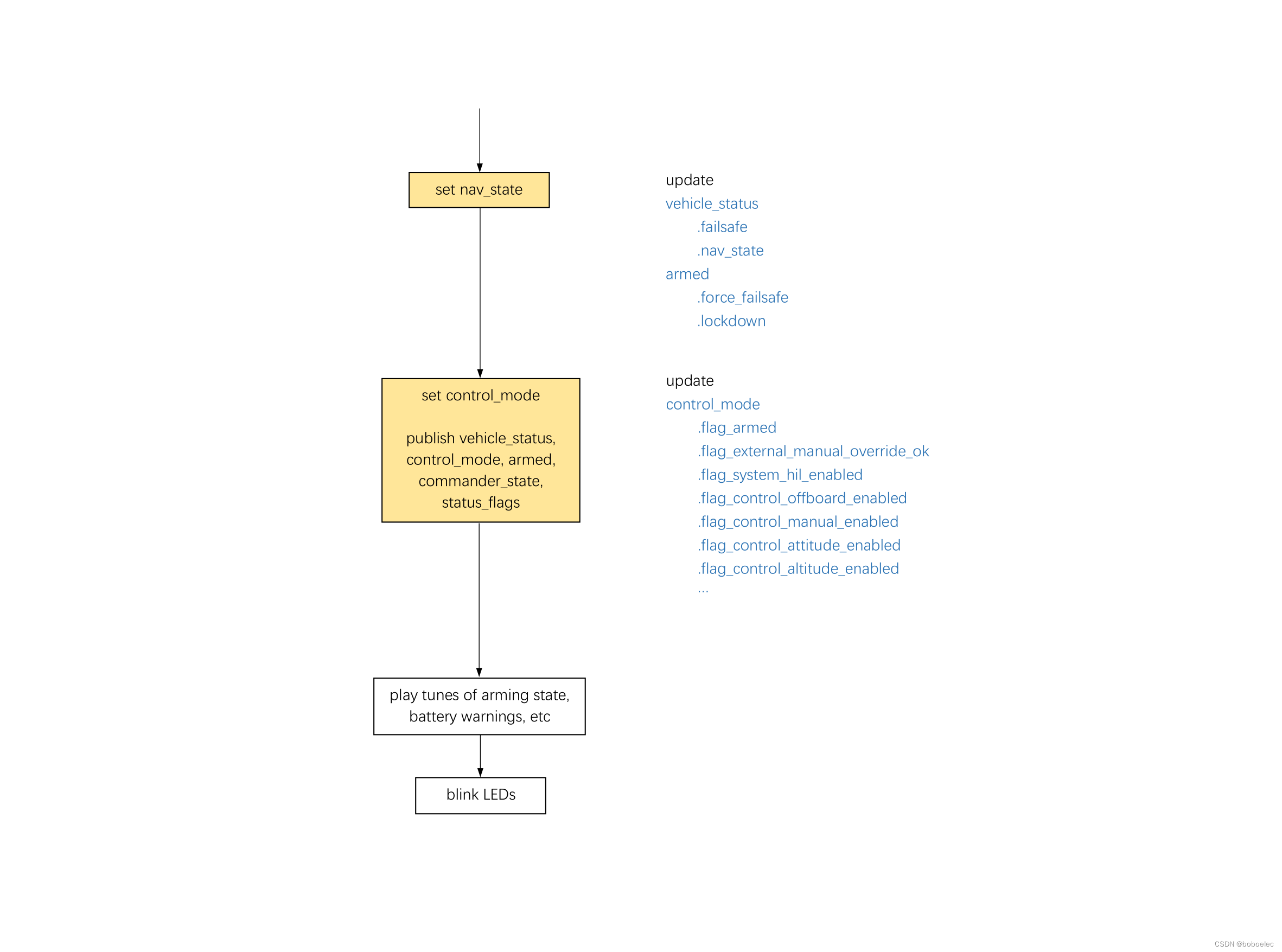
1、假设检验预备知识

• Z分位数
• 样本均值的分布
• 标准误

参考： 概率论：样本与总体分布，Z分数与概率_格勒王的博客-CSDN博客如何理解样本和整体的关系，利用Z分位数来品评估样本是否能够代表总体，这是假设检验的基础，当年就是没有完整理解这一点，导致概率论学的一知半解的https://blog.csdn.net/weixin_47198715/article/details/130872351?spm=1001.2014.3001.5501

2、假设检验说明

使用样本均值来评估一个未知总体均值的假设，目的是确定某种处理（实验变量）对于总体中的个体是否有效应（另均值加减某一个常量）

例如：针对一组随机抽样用户进行补贴实验，补贴前用户消费金额是100，补贴后的消费金额是105，那么是否证明增加补贴是否能提升转化率，提升的效果如何？

3、假设检验过程

3.1、提出假设：

• 原假设：补贴没有效果，加补贴之后转化率和总体无差别
• 备择假设：补贴有效果，加补贴之后转化率不等于总体（*注意，这里如果是不等于就是双侧假设检验，如果是大于或者小于就说明是单侧假设检验）

3.2、评估样本均值在总体分布中的位置，样本均值Z分位数

3. 3、确定显著性水平和拒绝域

显著性水平α是指样本均值出现在总体中的概率小于多少时，拒绝原假设，认定处理有效

拒绝域根据显著性水平划分拒绝域，如果显著性水平等于5%，那么拒绝域就是总体分布两端各±2.5%的面积，进而在标准差分布表中找到对应的Z分位数

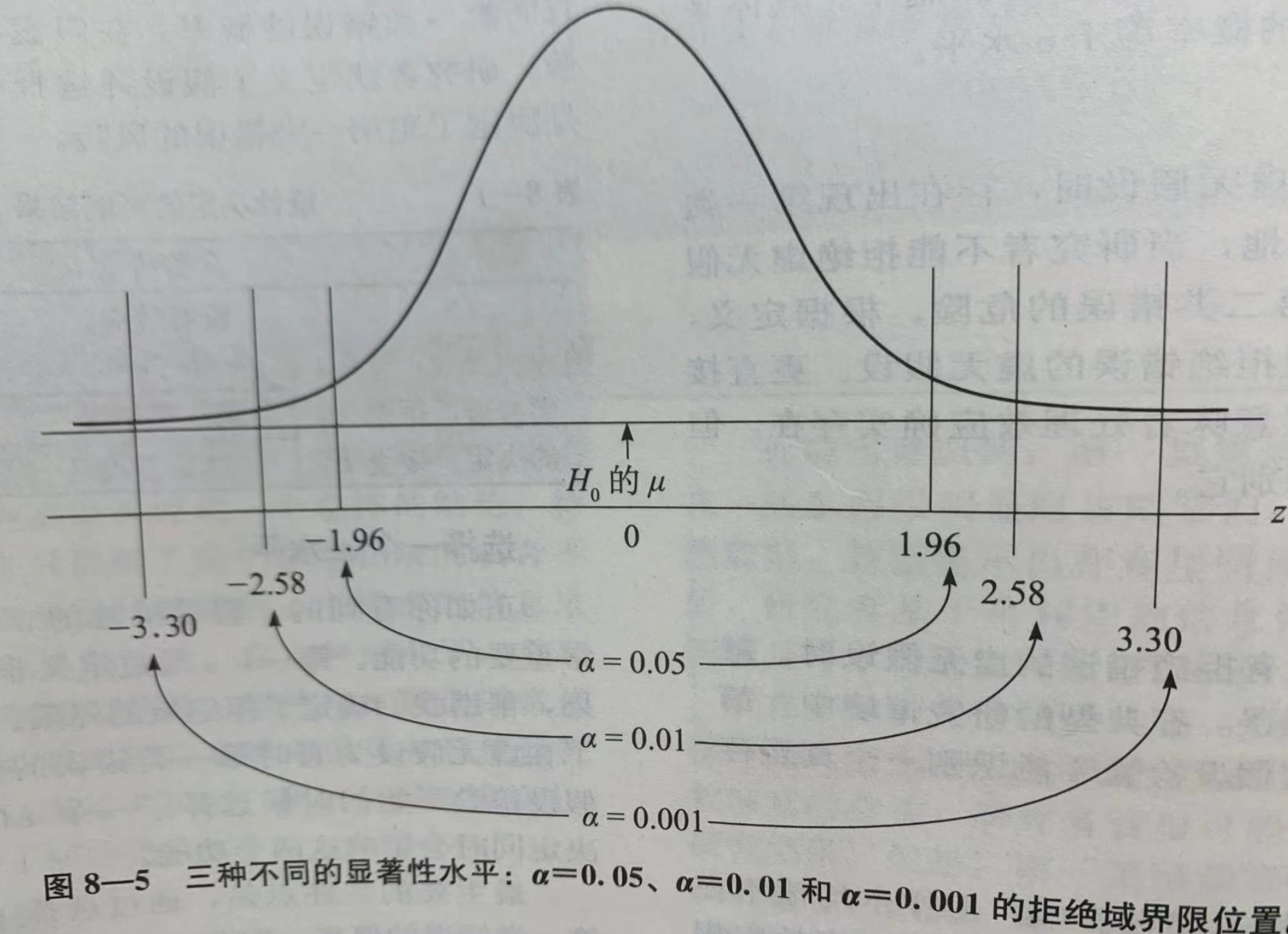 注意：单侧假设检验和双侧假设检验下，显著性水平对应的Z分位数值是不同的

3.4、比较样本均值Z分位数和拒绝域对应的Z分位数，得到结论

4、假设检验效应大小评估

cohen’s d系数=均值差异/标准差

含义：处理效果等于多少个标准差

 

5、假设检验的二类错误

	没有效果	有效果
接受H0（认为没有效果）	正确	第二类错误
拒绝H0（认为有效果）	第一类错误	正确

显著性水平的值α就是在原假设为真时（没有效果）拒绝原假设的概率。α需要尽可能的小，一般不会大于5%

6、适用情况

适用Z分位数假设检验的前提

• 随机样本且样本结果之间独立不相互影响
• 总体符合正态分布
• 默认处理后的标准差和总体标准差一致