B. 广告投放

Problem - B - Codeforces

 

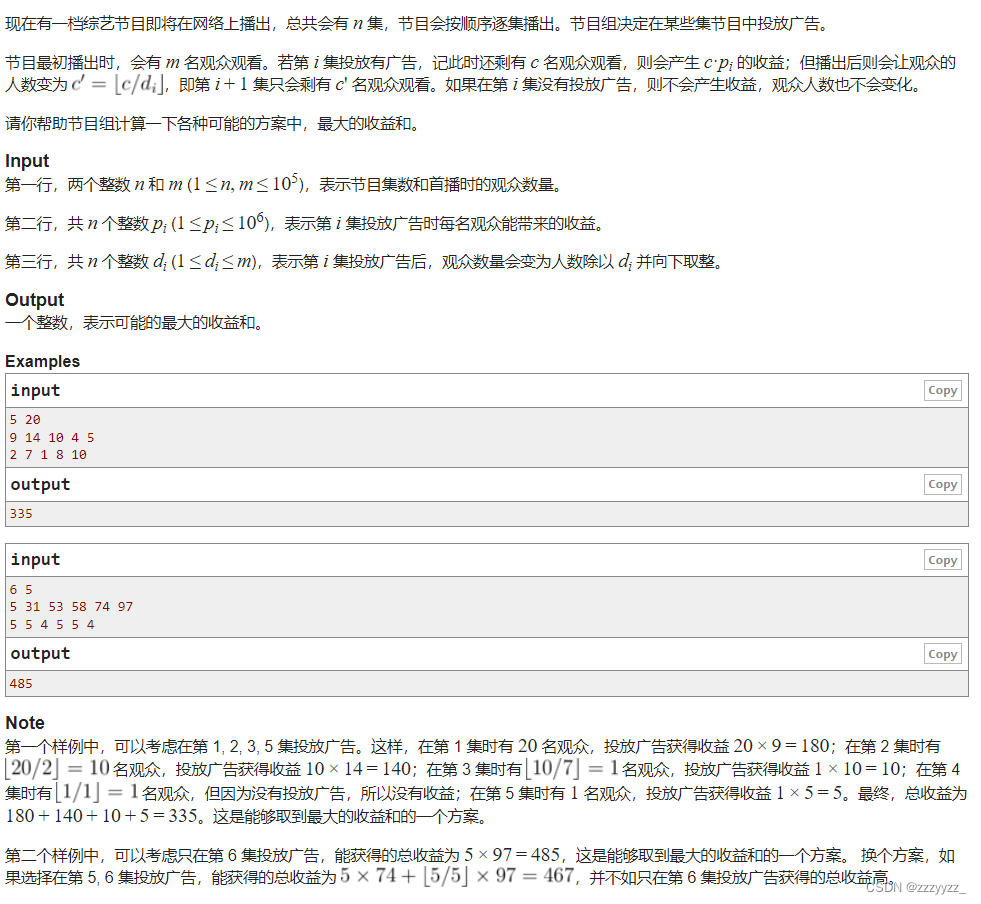
思路：对于这个题来说，我们很容易可以想到是一个dp问题，我们可以使用f[i][j]表示我们已经处理了前i-1个问题，并且当前剩余的人数是j的情况下，能够得到的最大的收益，那么对于f[i][j]来说，他又两种选择第一种是不播放广告，则f[i][j]-->f[i+1][j]，第二种情况是播放广告，则

f[i][j]-->f[i+1][j/d[i]]+j*p[i]，但是我们如果直接这样做会出现两种问题mle，tle，而对于mle来说，我们能够发现可以使用滚动数组优化掉一维，而对于tle来说，我们就需要进行其他的优化，我们观察转移方程发现，对于第二种转移来说，它可以转移到的位置就是j/d[i]不同的位置，而j是从1到m的，所以我们只需要先找到有多少个不同的位置，然后直接枚举不同的位置，这样能够去掉重复的枚举

// Problem: B. 广告投放
// Contest: Codeforces - 2020 CCPC Henan Provincial Collegiate Programming Contest
// URL: https://codeforces.com/gym/104095/problem/B
// Memory Limit: 512 MB
// Time Limit: 2000 ms

#include<iostream>
#include<cstring>
#include<string>
#include<sstream>
#include<cmath>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<map>
#include<stack>
#include<vector> 
#include<set>
#include<unordered_map>
#include<ctime>
#include<cstdlib>
#define fi first
#define se second
using namespace std;
typedef long long ll;
typedef double db;
typedef pair<int,int> PII;
typedef pair<int,pair<int,int> > PIII;
const double eps=1e-7;
const int N=5e5+7 ,M=5e5+7, INF=0x3f3f3f3f,mod=1e9+7;
const long long int llINF=0x3f3f3f3f3f3f3f3f;
inline ll read() {ll x=0,f=1;char c=getchar();while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') {x=(ll)x*10+c-'0';c=getchar();} return x*f;}
inline void write(ll x) {if(x < 0) {putchar('-'); x = -x;}if(x >= 10) write(x / 10);putchar(x % 10 + '0');}
inline void write(ll x,char ch) {write(x);putchar(ch);}
void stin() {freopen("in_put.txt","r",stdin);freopen("my_out_put.txt","w",stdout);}
bool cmp0(int a,int b) {return a>b;}
template<typename T> T gcd(T a,T b) {return b==0?a:gcd(b,a%b);}
template<typename T> T lcm(T a,T b) {return a*b/gcd(a,b);}
void hack() {printf("\n----------------------------------\n");}

int T,hackT;
int n,m,k;
int p[N];
int d[N];
vector<int> vis;
ll f[2][N];

void solve() {
	n=read(),m=read();

	for(int i=1;i<=n;i++) p[i]=read();
	for(int i=1;i<=n;i++) d[i]=read();
	
	for(int i=1;i<=m;i++) vis.push_back(m/i);
	vis.push_back(0);
	sort(vis.begin(),vis.end());
	vis.erase(unique(vis.begin(),vis.end()),vis.end());
	for(int i=1;i<=n;i++) {
		for(int j=0;j<vis.size();j++) {
			int x=vis[j];
			f[(i+1)&1][x]=max(f[(i+1)&1][x],f[i&1][x]);
			f[(i+1)&1][x/d[i]]=max(f[(i+1)&1][x/d[i]],f[i&1][x]+(ll)x*p[i]);
		}
	}
	
	ll res=0;
	for(int i=0;i<=m;i++) res=max(res,f[(n+1)&1][i]);
// 	
	printf("%lld\n",res);
}   

int main() {
    // init();
    // stin();

    // scanf("%d",&T);
    T=1; 
    while(T--) hackT++,solve();
    
    return 0;       
}