目录
1、什么是浮点数
2、浮点数与整数存储方式相同吗?
3、浮点数的存储规则
3.1 、国际标准IEEE(电气和电子工程协会) 754
3.2、IEEE 754规定:
3.3、IEEE 754对有效数字M的规定。
3.4、IEE 754对有效数字E的规定
E不全为0或不全为1
E全为0
E全为1
4、解释前面的题目
1、什么是浮点数
首先,我们需要理解什么是浮点数?
之前我们学习了定点数,其中「定点」指的是约定小数点位置固定不变。那浮点数的「浮点」就是指,其小数点的位置是可以是漂浮不定的。
这怎么理解呢?
其实,浮点数是采用科学计数法的方式来表示的,例如十进制小数 8.345,用科学计数法表示,可以有多种方式:
8.345 = 8.345 * 10^0
8.345 = 83.45 * 10^-1
8.345 = 834.5 * 10^-2
...看到了吗?用这种科学计数法的方式表示小数时,小数点的位置就变得「漂浮不定」了,这就是浮点数名字的由来。
使用同样的规则,对于二进制数,我们也可以用科学计数法表示,也就是说把基数 10 换成 2 即可。
2、浮点数与整数存储方式相同吗?
博主特意将浮点数与整数分开讲,那么说明肯定是不同的
这里博主为大家引入一个例子,看看是否真的不同,请看以下代码
int main()
{
int n = 9;
float *pFloat = (float *)&n;//将n的地址取出强制类型转换为float*,然后再赋给*pFloat
printf("n的值为:%d\n",n);
printf("*pFloat的值为:%f\n",*pFloat);
*pFloat = 9.0;
printf("num的值为:%d\n",n);
printf("*pFloat的值为:%f\n",*pFloat);
return 0;
}这里博主想让各位先试一下自己猜测一下结果为多少,我相信大多数都会猜测为
n的值为:9
*pFloat的值为:9.000000
num的值为:9
*pFloat的值为:9.000000
因为这是我们前面所讲的整数的存储思维,那这样的结果对吗?我们来看一下运行结果

我们发现,和我们猜想得值不一样,那这说明一个什么问题呢?
说明浮点数与整数得存储方式并不相同,接下来我们一起来看看浮点数再内存中是如何存储的
3、浮点数的存储规则
3.1 、国际标准IEEE(电气和电子工程协会) 754
我们已经知道,浮点数是采用科学计数法来表示一个数字的,它的格式可以写成这样:
V = (-1)^S * M * R^E其中各个变量的含义如下:
- S:符号位,取值 0 或 1,决定一个数字的符号,0 表示正,1 表示负
- M:尾数,用小数表示,例如前面所看到的 8.345 * 10^0,8.345 就是尾数
- R:基数,表示十进制数 R 就是 10,表示二进制数 R 就是 2
- E:指数,用整数表示,例如前面看到的 10^-1,-1 即是指数
3.2、IEEE 754规定:

- 符号位 S 占 1 bit
- 指数 E 占 10 bit
- 尾数 M 占 21 bit
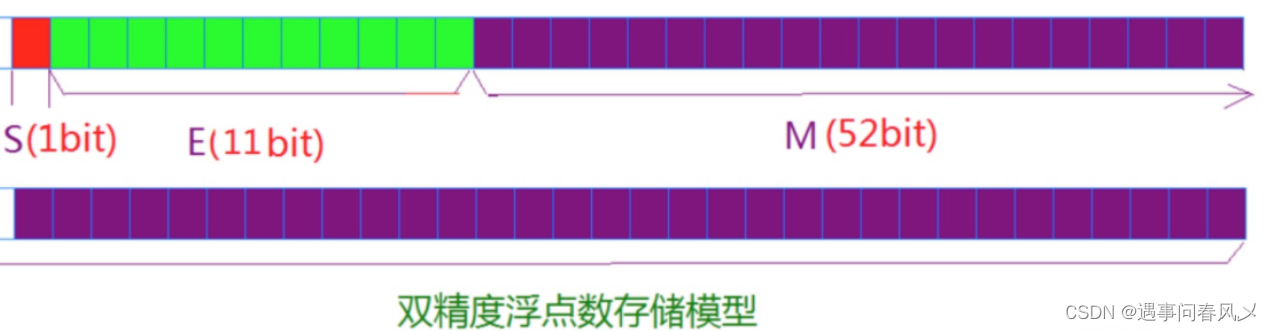
- 符号位 S 占 1 bit
- 指数 E 占 11 bit
- 尾数 M 占 52 bit
3.3、IEEE 754对有效数字M的规定。
3.4、IEE 754对有效数字E的规定
十进制:0.5
二进制:0.1
0.5=(-1)^0*1.0*2^(-1)
S:0
M:1.0
E:-1所以IEEE 754规定,存入内存时E的真实值必须再加上一个中间数,对于8位的E,这个中间数
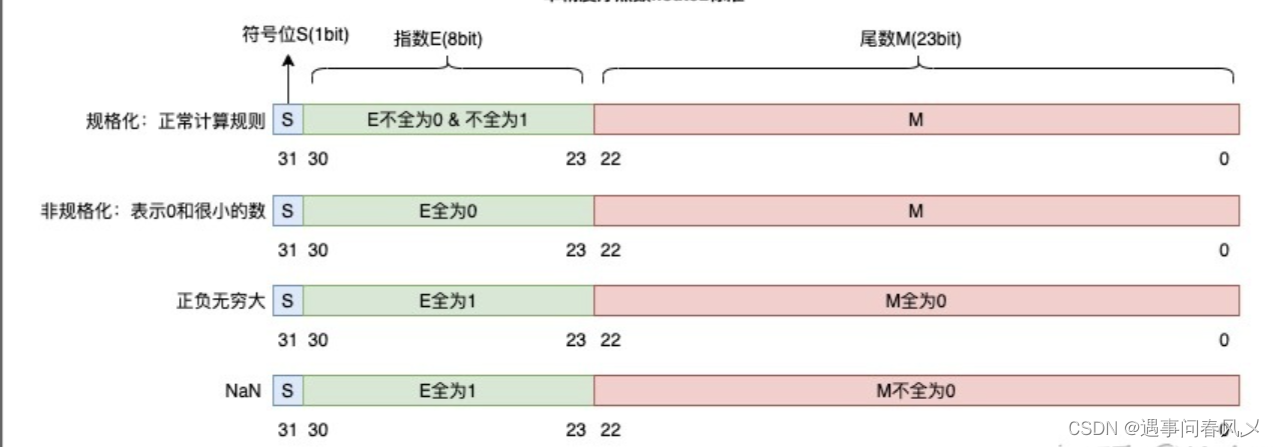
E不全为0或不全为1
E全为0
| S | E | M |
| 0 | 01111110 | 00000000000000000000000 |
E全为1
4、解释前面的题目
#include <stdio.h>
//
//int main()
//{
// int n = 9;
// //
// //0 00000000 00000000000000000001001
// //S E M
// //0 -126 0.00000000000000000001001
// //(-1)^0 * 0.00000000000000000001001 * 2^-126
// //
// //E在内存中是全0
// //
// float* pFloat = (float*)&n;
//
// printf("n的值为:%d\n", n);//9
// printf("*pFloat的值为:%f\n", *pFloat);//0.000000
//
// *pFloat = 9.0;
// //1001.0
// //1.001 * 2^3
// //(-1)^0 * 1.001 * 2^3
// //S=0 E=3 M=1.001
// //0 10000010 00100000000000000000000
// //
// printf("num的值为:%d\n", n);//1091567616
// printf("*pFloat的值为:%f\n", *pFloat);//9.0
//
// return 0;
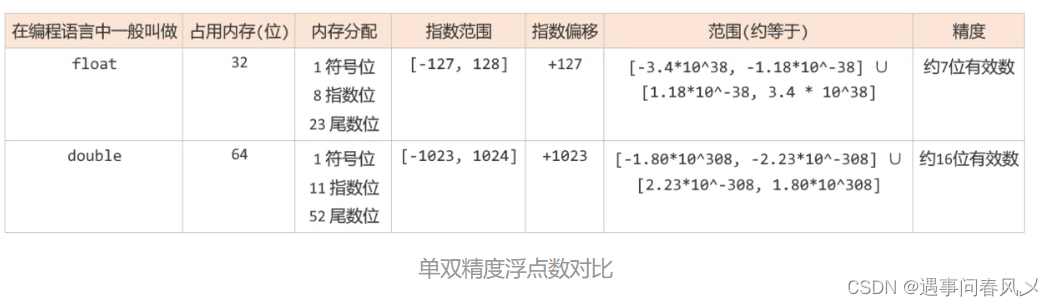
//}最后再给宝子们一个单双精度浮点数的对比,加深一下理解
制作不易,你的三连就是博主最大的动力!!!