插入排序(InsertionSort)
插入排序是一种简单直观的排序算法,它的基本思想是将待排序的元素插入到已经排好序的序列中,从而得到一个新的有序序列。插入排序的具体过程如下:
- 从第一个元素开始,认为它已经是有序的序列。
- 取出下一个元素,在已经排序的序列中从后向前扫描。
- 如果已经排序的序列中的元素大于新元素,将该元素移到下一个位置。
- 重复步骤3,直到已经排序的序列中的元素小于等于新元素。
- 将新元素插入到该位置后。
- 重复步骤2~5,直到所有元素都排序完成。
时间复杂度为O(n^2),空间复杂度为O(1),对于小规模的数据集来说,插入排序的效率是比较高的。
快速排序(QuickSort)
快速排序是一种基于分治思想的排序算法,它的基本思想是将待排序的序列分成两个子序列,其中一个子序列的所有元素都比另一个子序列的元素小,然后对这两个子序列分别进行排序,最终将它们合并成一个有序序列。快速排序的具体过程如下:
- 选择一个基准元素,通常是待排序序列的第一个元素。
- 将待排序序列分成两个子序列,其中一个子序列的所有元素都比基准元素小,另一个子序列的所有元素都比基准元素大。
- 对两个子序列分别进行快速排序,直到子序列中只剩下一个元素或为空。
- 将两个子序列合并成一个有序序列,其中基准元素放在两个子序列的中间位置。
时间复杂度为O(nlogn),最坏时间复杂度为O(n^2)
快速排序的效率比较高,因为它采用了分治的思想,可以将大规模的数据集分成小规模的数据集进行处理。
为了避免快速排序的最坏时间复杂度,可以采用随机化快速排序或者三路快排等算法来进行优化。
堆排序(HeapSort)
堆排序是一种基于堆的数据结构的排序算法,它的基本思想是将待排序的序列构建成一个堆,然后依次将堆顶元素取出来放入已排序序列中,最终得到一个有序序列。堆排序的具体过程如下:
- 将待排序的序列构建成一个堆,通常采用的是大根堆或小根堆。
- 将堆顶元素取出来,放入已排序序列中。
- 将堆的最后一个元素移动到堆顶,然后重新调整堆,使其满足堆的性质。
- 重复步骤2~3,直到堆中的元素全部取出来。
时间复杂度为O(nlogn),空间复杂度为O(n)
堆排序的效率比较高,因为它采用了堆的数据结构,可以快速的找到堆中的最大或最小元素。
堆排序是一种不稳定的排序算法,因为在构建堆的过程中可能会改变相同元素的相对位置。
对比
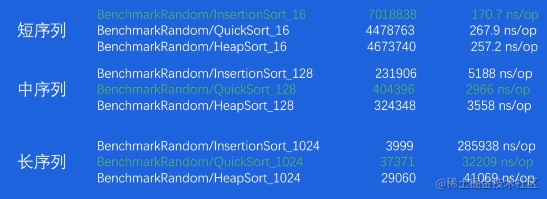
随机的情况下对比:
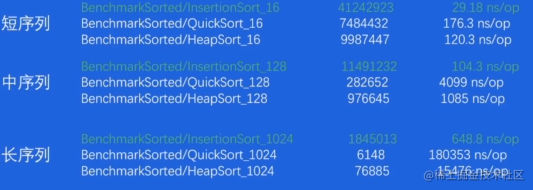
序列本身有序的情况下对比:
结论
- 插入排序在短序列和序列有序的情况下最快
- 大部分情况下,快速排序由较好的综合性能
- 堆排序在任何情况下表现都比较好
pdqsort —— pattern-defeating-quicksort
pdqsort是一种快速、原地、稳定的排序算法,它是由Orson Peters于2019年提出的。pdqsort的原理是基于经典的快速排序算法,但它采用了一些新的技术来提高性能和稳定性。
pdqsort的主要思想是将快速排序分为两个阶段:
- 快速排序
- 插入排序
-
在快速排序阶段,pdqsort使用经典的快速排序算法,选择一个中间元素作为枢轴(pivot),将数据分为两个子序列,并递归地对这两个子序列进行排序。但是,pdqsort在选择枢轴时采用了一些新的技术,如三点中值法(median-of-three),以避免最坏情况的发生。
-
在插入排序阶段,pdqsort使用插入排序算法对小的子序列进行排序。插入排序是一种简单而有效的排序算法,它对小的子序列的排序效果很好。pdqsort通过在快速排序阶段和插入排序阶段之间进行平滑的转换,来保持排序的稳定性。
pdqsort还采用了一些其他的技术来提高性能和稳定性,如分区排序(partition sort)和双轴快速排序(dual-pivot quicksort)。这些技术使得pdqsort在处理大量数据时具有很好的性能,并且可以保持排序的稳定性。





![[架构之路-202]- 常见的需求获取技术=》输出=》用户需求、客户需求(As...., I want.....)、用例图](https://img-blog.csdnimg.cn/23fcc0dfdc42409d88f1a84aaad49d32.png)