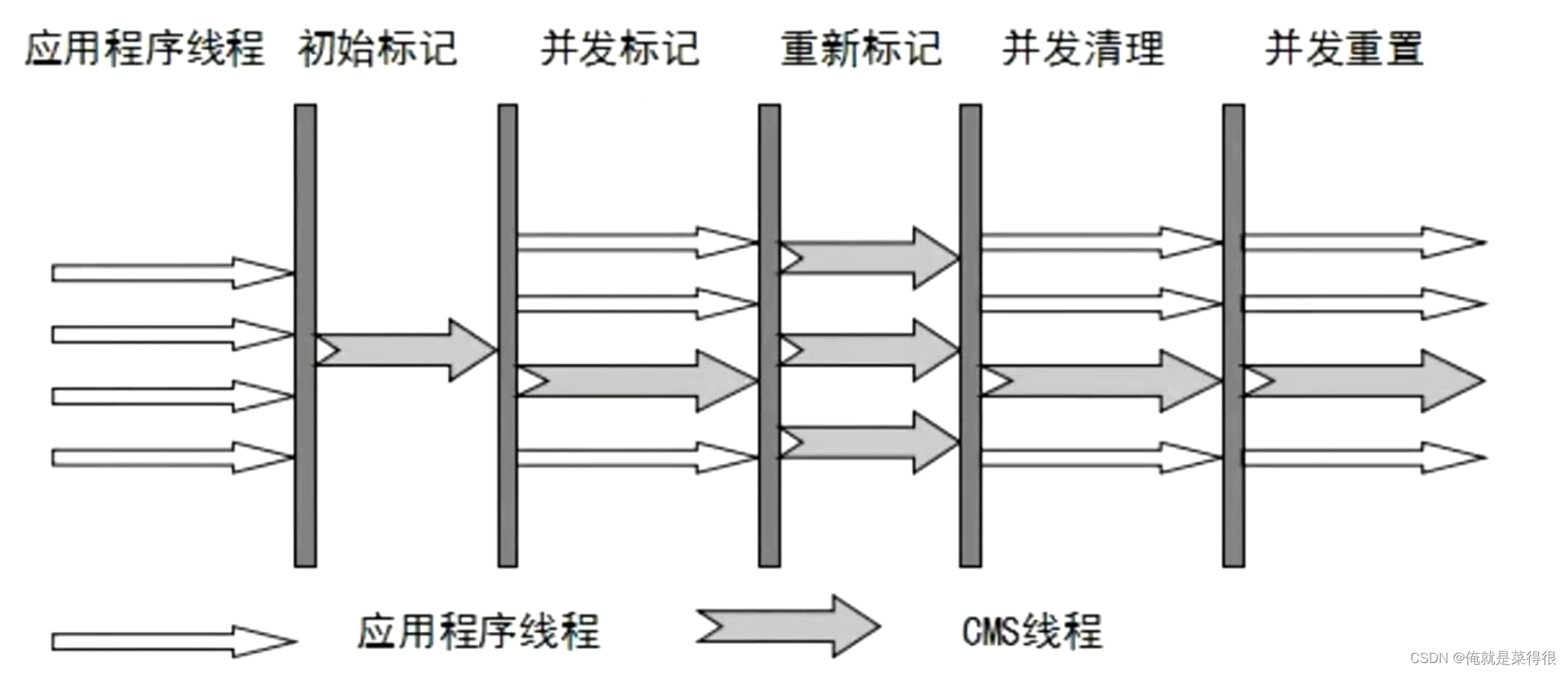
Gouraud是一种插值方法,Gouraud着色法是计算机图形学中的一种插值方法,可以为多边形网格表面生成连续的明暗变化。实际使用时,通常先计算三角形每个顶点的光照,再通过双线性插值计算三角形区域中其它像素的颜色。
在图形处理器流水线中,一般有几种着色方法:
固定着色(Pure shading, Constant shading)
按照人工的方法给定片元着色器颜色值
恒定着色(Flat shading)
通过一定方法,计算出每一个多边形的最终颜色,没有变化和插值
多用于实现卡通风格

《Minecraft》就是用的恒定着色
高洛德着色(Gouraud Shading)
通过计算顶点颜色,然后通过插值方法完成着色,在一个面上面也就可以有不同的颜色了

每一个顶点做一次光照计算,然后每一个三角形根据组成它的三角形进行插值给片段进行着色,计算非常快
《Final Fantasy VII》就是用的Gouraud Shading
冯氏着色(phone Shading)
包含ambient,diffuse,specular部分
每一个图元逐像素的法线进行光照计算,计算量较大,但是效果最好

高洛德着色(Gouraud Shading)的优缺点
优点:只计算顶点的光照,计算快
缺点有下面几个:
高光区丢失:
如果在多边形的中心有高光,而且这个高光没有扩散到该多边形的任何顶点,使用Gouraud着色法就不会渲染出任何效果,如下图周围的顶点没有得到这个计算值,这块也就不可能产生高光效果,不过可以通过提高顶点数去解决

高光区不正常:
另外,而如果正好是多边形的顶点上有高光,那么这个点上的高光是正确的,但插值会导致高光以很不自然的形式扩散到相邻的多边形上,这个大大的五角形:

亮度信息不对:
假设有这么一个场景,下面有个三角形片元,在片元上方正好有一个光源
我们把三角形平着倾斜过来:
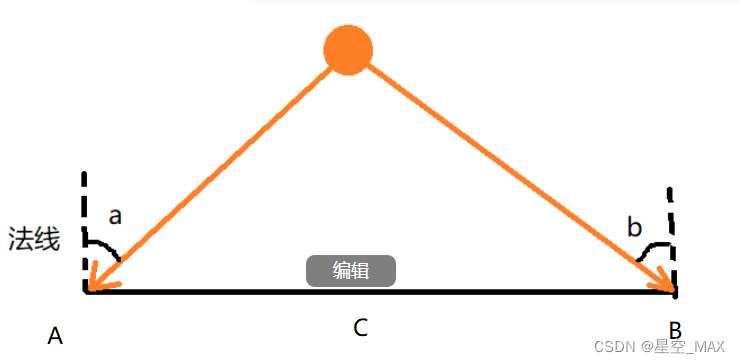
根据光照公式的点乘部分计算
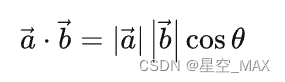
C点的光照强度等于A点的光照强度和B点光照强度的插值
当a和b的夹角越小的时候,得到的光照强度越大,也就是C点的光照越强
但当把光源向下移动的时候:
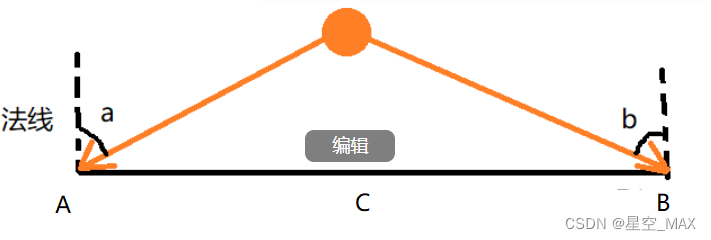
a和b的夹角更大了,这就意味着A和B的光照强度降低,所以根据A点和B点得到C点的光照也会减弱
光离面越近,这个面就会暗
这明显是个错误结果,但是随着面数的增加或者使用曲面细分着色器对面进行曲面细分,则可以减少它的缺点