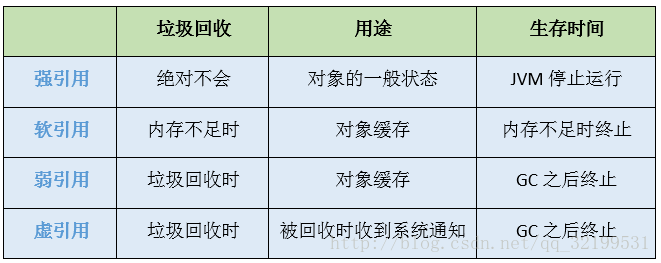
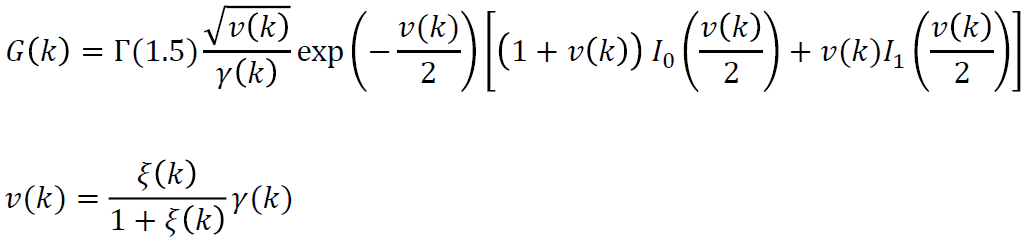1.森林的定义:m>=0 颗互不相交的树的集合
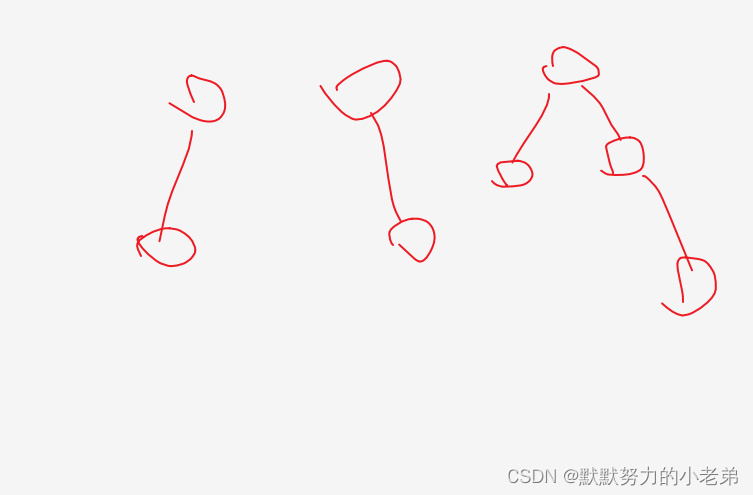
//树和森林的区别
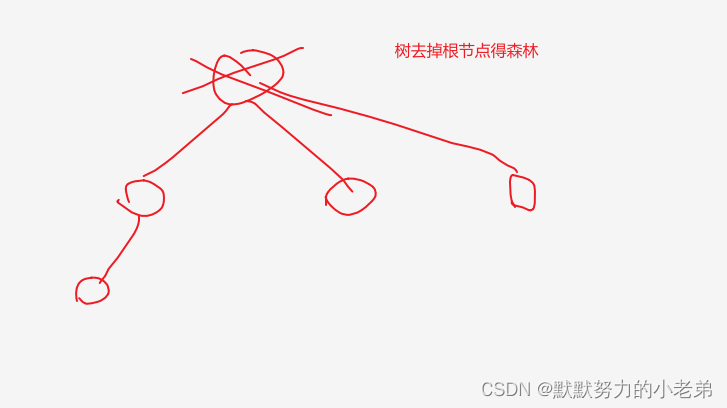
2.森林的遍历 for森林里的树(前序和后序遍历)
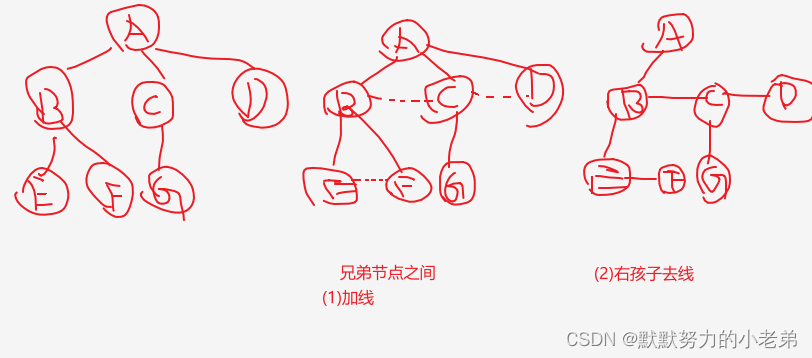
3.树转二叉树(兄弟连起来,去右线)
1.兄弟之间加线(树和树之间不加)
2.右孩子去线(只保留第一个结点的线)
3.顺时针调整45度位置变成二叉树
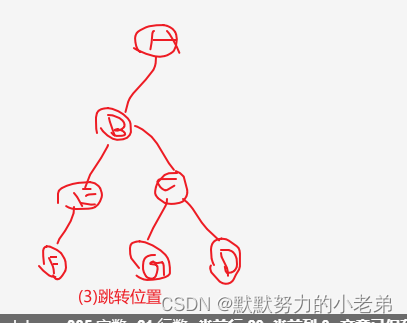
4.森林转二叉树
1.树(全部的树依次)转二叉树
2.第一棵不动
3.第一棵的右边根节点连接第二棵的根节点,然后第2棵根节点连接第3棵的根节点
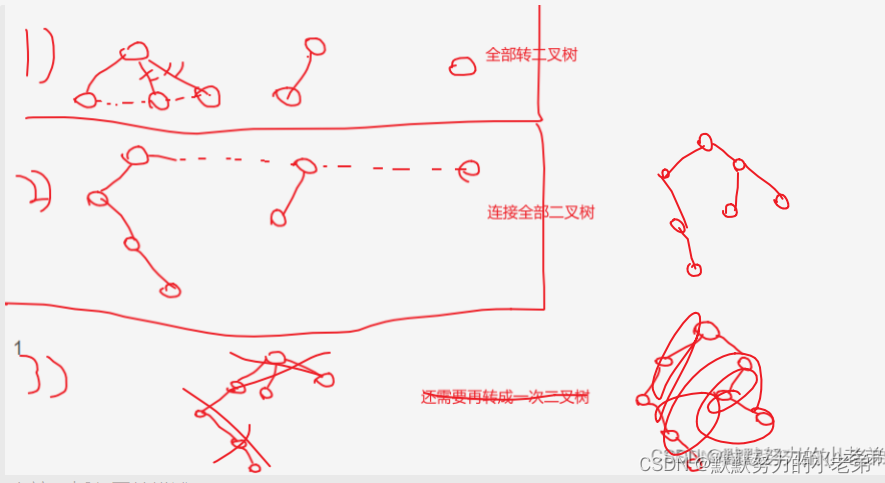
5.二叉树转树(去右孩子,连接右孩子[可以连接所有右孩子]) 上面的例子举例(连接上面去下面,与树转二叉树过程相反)
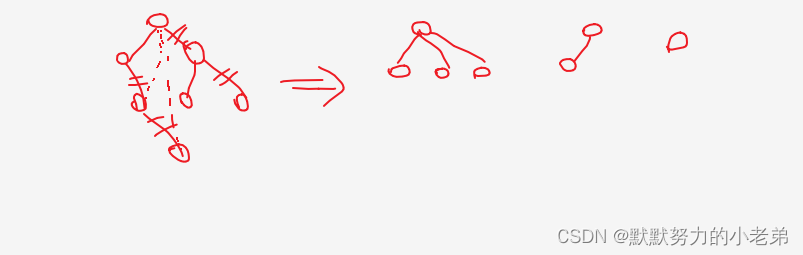
6.最优二叉树(哈夫曼树): 带权路径长度最小的二叉树(哈夫曼编码,是哈夫曼发明的)
1.权值: 叶子节点加个数字
带权路径长度(WPL Weighted Path Length): 求和 (根节点到叶的边数 * 权值) 如
A//这是最优二叉树(权值最小) 假设我们要发送信息是2 3 4,必须要编为0或1的二进制串

//这不是最优的

7.哈夫曼编码有什么用? 发消息如果不是最小权值(哈夫曼树)发消息会更费带宽(因为计算机是以二进制发送消息的)
8.哈夫曼编码的特点:
- 权值越大,离根节点更近
- 只有度为0和2的,没有度为0的
9.如何构造一颗最优二叉树? 给几个节点的权(其实代表发送的数据,想要最小网络带宽传输一段二进制)(一个最小WPL对应有多颗树,所以可能生成不同的样子)
1.找到最小的两个组合生成他们的节点,父节点的权为他们的和
2.在所有为组合的节点选最小的两个组合(包括新生成的父节点)
如:
A: 10 B: 8 C: 19 D:4 E:6 F:25
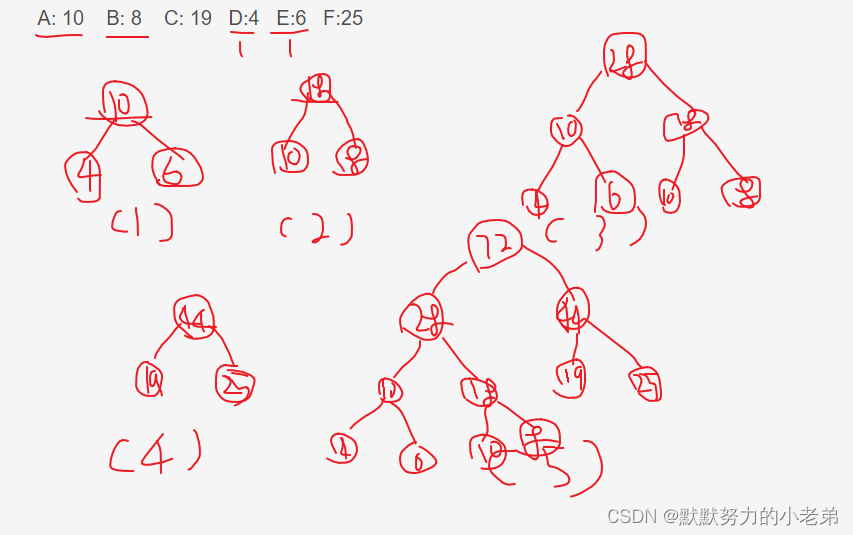

10.编码和解码
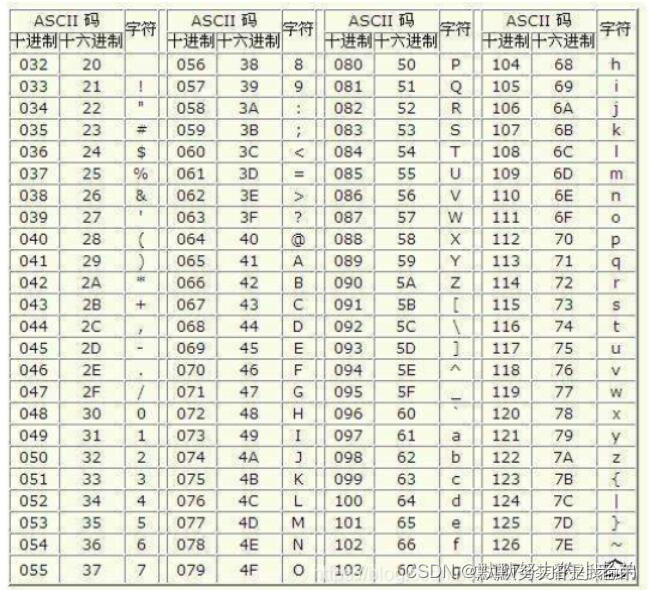
- 等长编码: 如 ASCII码是3位的
不等长编码: 如哈夫曼编码 编出来的长度不唯一- 解码: 有唯一性 需要满足任一编码不是其他编码的前缀(不重复);哈夫曼编码有唯一性
编码: 没有唯一性