过度拟合
我们来想象如下一个场景:我们准备了10000张西瓜的照片让算法训练识别西瓜图像,但是这 10000张西瓜的图片都是有瓜梗的,算法在拟合西瓜的特征的时候,将西瓜带瓜梗当作了一个一般性的特征。此时出现一张没有瓜梗的西瓜照片,算法就认为它不是西瓜了。这种情况被称为过拟合。
上面从感性的方面感受了下过拟合的情况,接下来我们系统分析过拟合的情况。还是以我们经典的通过房屋大小预测房价走向的问题,假设有以下三个拟合好的图像
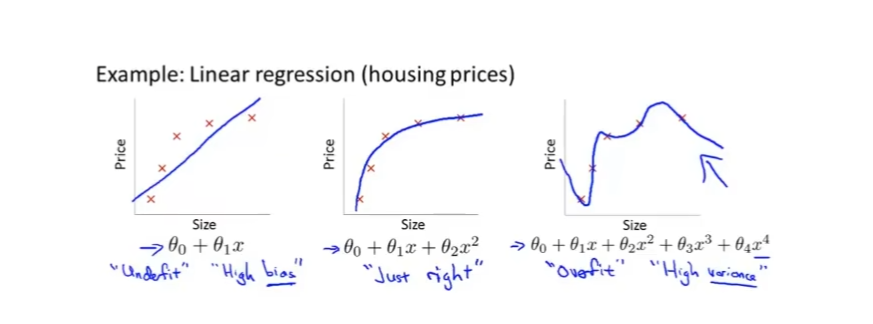
首先看左边的图像,他只使用了一个一元一次方程去拟合,很明显它的预测效果并不是那么的好,预测出来结果有一定误差,这被称之为欠拟合,其特征是具有高偏差。
中间的图像使用了一个二次方程,拥有较好的拟合效果。
最后看右边的图像,它使用一个四次方函数进行拟合。它完美地经过了所有的样本点,它的代价函数J=0,但是它实际上的预测效果并不好:有些面积大的房子反而价格低,有些面积小的房子反而价格很高,这就是过拟合,过拟合的结果是模型的泛化效果很差,算法如同刻舟求剑一样只能正确预测训练集中的数据,对其他数据的预测结果有较大的偏差,这也称之为高方差。(这里就不得不说下奥卡姆剃刀定律——如无必要,勿增实体。中间的模型在相对简单的情况下就完成了较好的模拟,那我们就没必要再去搞更复杂的模型了)
同样的例子也可以用于逻辑回归
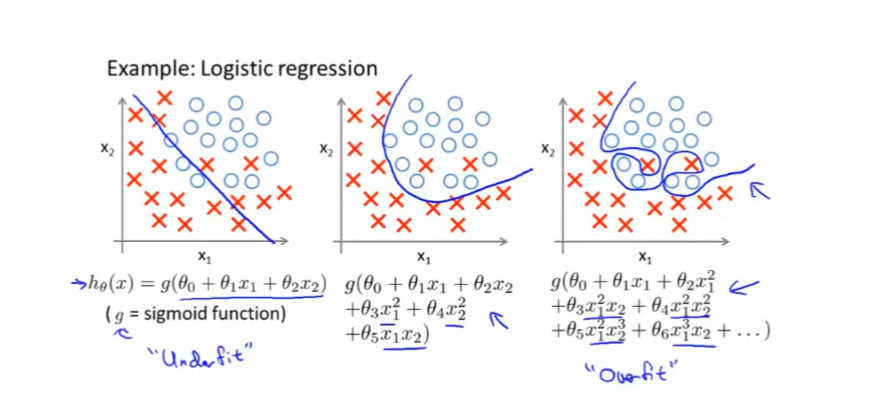
右图也是一个过拟合的模型,感觉就像是用力过猛了
如何避免
要知道如何避免首先我们要分析什么情况容易出现过拟合。
1.使用次方数过高的多项式进行拟合,这使得拟合曲线可以十分弯曲
2.加入了过多的相关参数,决定房价的因素有很多,包括大小、房间数等等,过多的参数也会导致过拟合
那么解决方法有两个:
第一个是减少特征的数量,可以自己手动剔除掉一些不需要的特征,也可以使用特征选择算法来让算法决定哪些特征需要保留。这样做的缺点是,会使得你的模型失去一部分的信息。
第二个是正则化,也是接下来我们需要学习的东西。正则化会保留所有特征但是会减少量级或者参数 θ j \theta_j θj的大小。接下来我们就要介绍正则化相关内容了