1. 引言
前序博客有:
- Nova: Recursive Zero-Knowledge Arguments from Folding Schemes学习笔记
- SuperNova:为多指令虚拟机执行提供递归证明
- 基于Nova/SuperNova的zkVM
- Sangria:PLONK + Folding
- 2023年 ZK Hack以及ZK Summit 亮点记
- Sangria:类似Nova folding scheme的relaxed PLONK for PLONK
主要参考资料:
- 2023年4月视频 ZK Study Club: Supernova (Srinath Setty - MS Research)
- slides ZK Study Club: Supernova (Srinath Setty - MS Research)
Nova和SuperNova作者之一Srinath Setty在 ZK Study Club: Supernova (Srinath Setty - MS Research)中介绍了:
- 何为SuperNova
- SuperNova适于的场景
- SuperNova的工作原理
Nova代码实现见:
- https://github.com/Microsoft/Nova(Rust)
2. 何为SuperNova?
何为SuperNova?
- 1)是一种证明系统:Prover将proof
π
\pi
π发送给Verifier:

- 2)面向的是半结构化计算的证明:

实际半结构化计算可用于如下场景:- EVM:证明EVM执行
- RISC-V:证明RISC-V CPU执行
- WebAssembly:证明WebAssembly CPU执行
- VDF
- zkML
- zkBridge
- PhotoProof

SuperNova的主要特点为:
- 1)SuperNova的Prover要比general zkSNARK Prover 更便宜。
- 2)SuperNova的Prover的per-step cost 与 所执行指令的电路size 成比例。如虚拟机有数十条指令,每一步仅执行一条指令,Prover在该step的开销 仅与 所执行指令的电路size 成比例,而与其他如等无关。
- 3)基于folding schemes构建:将具有相同结构的2个电路(各自有不同的input),”合并“为一个电路folded instance,而不是证明这2个电路instance的satisfiability。folding是不昂贵的,在证明最终的folded instance之前,可以根据需要做任意次合并——这也是节约Prover开销的关键所在——”只合并,不证明“。

3. SuperNova适于的场景
当前使用的succinct arguments的演变过程为:
- 1)基于Linear PCPs + Linear-only encodings的方案,代表有:【具有shortest proofs,需要Per-circuit trusted setup】
- 1.1)quadratic Prover(最坏情况):
- Pepper [SBW11, SMBW12]
- Ginger [SVP+12]
- 1.2)quasilinear Prover(QAP-based linear PCP):
- [GGPR13]
- Zaatar [SBV+13], [BCIOP13]
- Pinocchio [PGHR13]
- [Groth16]
- 1.1)quadratic Prover(最坏情况):
- 2)基于Polynomial IOPs + Polynomial commitment schemes的方案,代表有:【Universal/untrusted setup,具体取决于所采用的多项式承诺方案。具有可定制化的电路表示。】
- 2.1)non-succinct Verifier(最坏情况):【因Verifier需读取circuit description】
- [CMT12] [VSBW13] [T13]
- Aurora [BCR+18]
- vSQL [ZGK+17]
- Hyrax [WTs+18]
- Stark [BBHR18]
- 2.2)succinct Verifier(computation commitments/holography):【Verifier仅需电路本身的succinct encoding】
- 2.2.1)基于Multilinear多项式的方案有:
- Spartan [S19]
- Quarks [SL20]
- HyperPlonk [CCBZ23]
- SuperSpartan [STW23——Customizable constraint systems for succinct arguments]
- 2.2.2)基于单变量多项式的方案有:
- Sonic [MBKM19]
- Plonk [GWC19]
- Marlin [CHM+19]
- SuperMarlin [STW23——Customizable constraint systems for succinct arguments]
- 2.2.1)基于Multilinear多项式的方案有:
- 2.1)non-succinct Verifier(最坏情况):【因Verifier需读取circuit description】
- 3)基于Folding schemes的方案,代表有:【针对incremental circuits,具有最快的Prover。且易于对Prover进行并行化加速。同时具有上面”基于Polynomial IOPs + Polynomial commitment schemes的方案“ 的所有优势。】
- 3.1)(S)NARK recursion:
- [BCTV14]
- Halo [BGH19] [BCMS20] [BCL+20] [BDFG20]
- 3.2)(S)NARK-less recursion:
- Nova [KST21]
- SuperNova [KS22]
- Sangria:又名PlonkNova [M23]
- HyperNova [KS23——HyperNova: Recursive arguments for customizable constraint systems]
- 3.1)(S)NARK recursion:

上图中红色标识的S均标识Srinath Setty为作者之一。
4. SuperNova的工作原理
SuperNova为:
- 将Nova推广至半结构化电路(或半结构化计算)。
最终目标是:
- 为结构化计算构建fast zkSNARKs方案。
- 证明:基于初始输入
z
0
z_0
z0,运行某non-deterministic computation
C
C
C
n
n
n次,最终结果为
z
n
z_n
zn。
所谓结构化计算,是指可将某计算分解为多个steps。使得存在circuit C C C,初始输入为 z 0 z_0 z0,每个step具有non-deterministic inputs W i W_i Wi,同时每个step还将前一step的输出作为输入,重复该step n n n次,最终结果为 z n z_n zn。

实际应用的场景有:
- 1)VDF: C C C为某delay函数(如MinRoot,计算用时为non-trivial sequential time)的一次或多次调用。
- 2)zkVM: C C C为某VM(如EVM/Wasm/LLVM)的某个step,或某CPU(如RISC-V)的某个step。
- 3)zkBridge: C C C为根据某链的共识规则来验证state。
- 4)zkML: C C C为ML模型上的某layer。
- 5)PhotoProof: C C C为对某图片的特定转换(如模糊、裁剪等)。
- 6)Public key directory: C C C检查某directory在每个epoch是否为append-only。WhatsApp近期声称采取该技术解决端到端加密中的key transparency 问题:Deploying key transparency at WhatsApp。
- 7)本文场景:用于半结构化计算,其中每个step为执行
{
F
1
,
F
2
,
⋯
,
F
l
}
\{F_1,F_2,\cdots,F_l\}
{F1,F2,⋯,Fl}中的某个函数。即每个step不再局限于固定相同的circuit,每个step可为预定义列表中某个可能的circuit。
整个执行是顺序执行的,但proof生成过程可并行化(如使用binary tree结构)。本文将忽略binary tree的优化,重点关注顺序执行的部分。
4.1 结构化计算证明的直观方案
直观方案为:将
C
C
C的
n
n
n次调用展开到单一电路中,并以某zkSNARK来证明。
这样会构建一个巨大的电路:以初始输入
z
0
z_0
z0和所有的non-deterministic inputs调用所有的
C
C
C,输出为output
z
n
z_n
zn。

直观方案的缺陷为:
- Prover需要巨大的内存: Ω ( n ⋅ ∣ C ∣ ) \Omega(n\cdot |C|) Ω(n⋅∣C∣)。
- 难于对proof生成过程进行并行化或分发加速。
- Verifier的验证时长可能会依赖 n n n。
- 相比于普通zkSNARK方案,并无法提供更快的Prover。
4.2 结构化证明的Valiant方案[Val08, BCTV14]——Incrementally Verifiable Computation
2008年,[Val08]提出了Incrementally Verifiable Computation(IVC)方案,不同于直观方案中直接证明最终计算结果,在IVC中,每个step不仅证明
C
C
C的调用,同时还在每个step的电路中添加一个Verifier——输入为前一step的输出
z
i
−
1
z_{i-1}
zi−1 和 proof
π
i
−
1
\pi_{i-1}
πi−1,输出为当前step执行正确的结果
z
i
z_i
zi 以及 对前一step proof验证正确 且 当前step执行正确 的proof
π
i
\pi_i
πi。

2019年[BGH19, BCMS20]中,将上述方案进一步衍化为:【将SANRK Verifier编码集成在Circuit中会引入额外的开销,因此Halo论文中改进为:采用累加机制,无需在每个step Circuit中集成完整的SNARK Verifier,可将SNARK中某些特定的昂贵的step推迟验证——累加为
U
i
U_i
Ui。】

每个step:
- Verifier V ′ V' V′仅验证部分proof π i − 1 \pi_{i-1} πi−1
- 更新accumulator U i U_{i} Ui
这种基于SNARK的IVC方案[BCTV14, BGH19, BCMS20],存在的缺陷为:
- 需要为 C C C的每次调用生成SNARK,因此最终的Prover速度 无法超过 所使用的SNARK方案的Prover速度。
- Verifier circuit仍相当大(大于 2 18 2^{18} 218个乘法门),引入大量的递归开销、
4.3 结构化证明的Nova方案
Nova方案避免了上述SNARK方案以及(non-succinct)arguments of knowledge方案的缺陷。
Nova的关键点为:
- 1)使用Non-interactive folding schemes 来实现 IVC。
- 2)对NP,存在a public coin, one-round folding scheme。
- 因在RO模式下可使其Non-interactive,在plain模式下,可对Non-interactive做启发式版本实现。
最终Nova的性能为:
- Nova Prover的开销要比通用SNARK方案便宜很多:如PLONK中需要22+个MSM运算以及一些FFT运算,而Nova中仅需要2个size为 O ( ∣ C ∣ ) O(|C|) O(∣C∣)的MSM运算(与circuit size成比例)。
- Nova的缺陷为其proof size为 O ( ∣ C ∣ ) O(|C|) O(∣C∣)(与circuit size成比例),不过可采用通用SNARK方案来压缩proof size。
4.3.1 Nova的基石——Folding schemes
假设Prover和Verifier具有某circuit
C
C
C,且具有2个待check的claims:

Folding scheme是以原始的2个instance(分别具有witness
w
1
,
w
2
w_1,w_2
w1,w2 和 public io
x
1
,
x
2
x_1,x_2
x1,x2)为输入,将其合并为一个folded output instance(具有新的witness
w
w
w 和 public io
x
x
x):

folding scheme应满足如下属性:
- 1)Completeness:若原始的2个instance时satisfiable的,则folding合并之后的folded output instance也是satisfiable的。
- 2)Knowledge soundness:若Prover知道folded output instance的witness w w w,则其必然知道原始的2个instance的witness w 1 , w 2 w_1,w_2 w1,w2。
- 3)Succinct:Verifier的验证开销 应小于 直接检查2个原始instance的开销。
- 4)ZK:除输入输出instance之外,整个交互过程不泄露其它信息。
事实上,zkSNARKs trivially提供了一种folding scheme实现:【如之前图片中的Halo、[BCMS20]等accumulation方案】
- 即先证明第一个instance C ( w 1 , x 1 ) = 1 C(w_1,x_1)=1 C(w1,x1)=1
- 然后再证明第一个instance
C
(
w
2
,
x
2
)
=
1
C(w_2,x_2)=1
C(w2,x2)=1

不过Nova的目的是设计一种无需SNARKs甚至non-succinct NARKs的folding scheme。
4.3.1.1 Nova采用R1CS电路表示[GGPR13]
R1CS电路表示首次在[GGPR13]论文中含蓄提出。其要素主要为:
- 电路描述:矩阵 A 、 B 、 C A、B、C A、B、C
- Public input: x x x
- witness: W W W
- 电路所满足的relation:即有向量
Z
=
(
W
,
x
,
1
)
Z=(W, x, 1)
Z=(W,x,1),满足:【其中
∘
\circ
∘表示Hadamard product运算,详细可参看rank-1 constraint system R1CS。】

社区传说或观点:”R1CS时代已终结?“ - 1)PlonkNova(”Sangria“ [M23]):可将Nova扩展至degree为2的Plonk电路表示。详细可参看博客:Sangria:类似Nova folding scheme的relaxed PLONK for PLONK。
- 2)[STW23——Customizable constraint systems for succinct arguments]中引入了CCS(Customizable Constraint System):在不引入额外开销overhead的情况下,为R1CS、PLONK、AIR电路的通用表示。
- 3)[KS23——HyperNova: Recursive arguments for customizable constraint systems]:将Nova扩展至CCS(Customizable Constraint System),从而也就扩展至了Plonk电路表示。
4.3.1.2 对R1CS Instance的fold尝试
引入随机值
r
r
r,做random linear combination:

不过,令
Z
i
=
(
W
i
,
x
i
,
1
)
Z_i=(W_i, x_i,1)
Zi=(Wi,xi,1),且
Z
=
Z
1
+
r
⋅
Z
2
Z=Z_1+r\cdot Z_2
Z=Z1+r⋅Z2,这样直接的random linear combination之后,有:
A
Z
∘
B
Z
≠
C
Z
AZ\circ BZ\neq CZ
AZ∘BZ=CZ
因:
C
Z
=
A
Z
1
∘
B
Z
1
+
r
⋅
A
Z
2
∘
B
Z
2
CZ = AZ_1\circ B Z_1 + r\cdot AZ_2\circ BZ_2
CZ=AZ1∘BZ1+r⋅AZ2∘BZ2
A
Z
∘
B
Z
=
A
Z
1
∘
B
Z
1
+
r
2
⋅
A
Z
2
∘
B
Z
2
+
r
⋅
(
A
Z
1
∘
B
Z
2
+
A
Z
2
∘
B
Z
1
)
AZ\circ BZ = AZ_1\circ B Z_1 + r^2\cdot AZ_2\circ BZ_2 + r\cdot (AZ_1\circ BZ_2 + AZ_2\circ BZ_1)
AZ∘BZ=AZ1∘BZ1+r2⋅AZ2∘BZ2+r⋅(AZ1∘BZ2+AZ2∘BZ1)
4.3.1.3 Relaxed R1CS:为folding引入的修正版R1CS
在Relaxed R1CS中,额外引入了:
- 一个error vector E E E:用于抵消交叉项 r ⋅ ( A Z 1 ∘ B Z 2 + A Z 2 ∘ B Z 1 ) r\cdot (AZ_1\circ BZ_2 + AZ_2\circ BZ_1) r⋅(AZ1∘BZ2+AZ2∘BZ1)。【注意error向量 E E E的长度等于 Z Z Z向量的长度,即 ∣ E ∣ = O ( ∣ W ∣ ) |E|=O(|W|) ∣E∣=O(∣W∣),因此Verifier为not succinct的。】
- 一个scalar u u u:用于解决 r ⋅ A Z 2 ∘ B Z 2 r\cdot AZ_2\circ BZ_2 r⋅AZ2∘BZ2 与 r 2 ⋅ A Z 2 ∘ B Z 2 r^2\cdot AZ_2\circ BZ_2 r2⋅AZ2∘BZ2 之间差的 r r r乘项。
当 E E E为零向量, u u u为scalar零值时,Relaxed R1CS等价为通用R1CS。
向量
Z
Z
Z变为
Z
=
(
W
,
x
,
u
)
Z=(W,x,u)
Z=(W,x,u),使得满足:

4.3.1.4 针对Relaxed R1CS的Folding Scheme(有问题版本)
认为 error vector
E
E
E 和 scalar
u
u
u 均与特定待证明的电路关联,将二者作为公开信息,对Prover和Verifier均已知。
针对Relaxed R1CS的Folding Scheme设计为:

基本流程为:【注意,
A
,
B
,
C
,
E
1
,
u
1
,
x
1
,
E
2
,
u
2
,
x
2
A,B,C,E_1,u_1,x_1,E_2,u_2,x_2
A,B,C,E1,u1,x1,E2,u2,x2均为公开信息,对Prover和Verifier都已知。】
- Prover:计算交叉项
T
=
A
Z
1
∘
B
Z
2
+
A
Z
2
∘
B
Z
1
−
u
1
⋅
C
Z
2
−
u
2
C
Z
1
T = AZ_1\circ BZ_2 + AZ_2\circ BZ_1 - u_1\cdot CZ_2-u_2CZ_1
T=AZ1∘BZ2+AZ2∘BZ1−u1⋅CZ2−u2CZ1
Prover将 T T T发送给Verifier。 - Verifier:发送随机challenge值 r r r。
- Prover:fold W = W 1 + r ⋅ W 2 W=W_1+r\cdot W_2 W=W1+r⋅W2,fold E = E 1 + r ⋅ T + r 2 ⋅ E 2 E=E_1+r\cdot T+r^2\cdot E_2 E=E1+r⋅T+r2⋅E2。
- 最终Prover和Verifier获得了单个folded instance,其witness为
W
W
W,公开信息为
(
A
,
B
,
C
,
E
,
u
,
x
)
(A,B,C,E,u,x)
(A,B,C,E,u,x)。
但是,该设计存在2个问题:- 1)Verifier无法enforce约束 Prover是否正确fold了 W W W。即无法保证completeness。
- 2)error向量 E E E的长度等于 Z Z Z向量的长度,即 ∣ E ∣ = O ( ∣ W ∣ ) |E|=O(|W|) ∣E∣=O(∣W∣),因此Verifier为not succinct的。
4.3.1.5 针对Relaxed R1CS的Folding Scheme(借助commitment同态属性的完美版)
认为 error vector E E E 和 scalar u u u 均与特定待证明的电路关联, E E E作为witness,将 u u u、 E ˉ \bar{E} Eˉ(error向量 E E E的承诺值)、 W ˉ \bar{W} Wˉ(witness W W W的承诺值)作为公开信息,对Prover和Verifier均已知。
针对Relaxed R1CS的Folding Scheme(借助commitment同态属性的完美版)设计为:

其中所采用的承诺方案应具有加法同态属性,如Pederson承诺等。
该设计方案:
- 同时具备completeness属性和knowledge soundness属性。
- 为succinct的:因Verifier仅需对多项式承诺值进行folding。
4.3.2 Nova的IVC方案实现
详情见Nova论文 5.1节内容,针对的IVC场景为:
初始输入
z
0
z_0
z0,运行
n
n
n次
F
F
F函数,输出为
z
n
z_n
zn。即
z
n
=
F
(
n
)
(
z
0
)
z_n=F^{(n)}(z_0)
zn=F(n)(z0)。

上图中NIFS表示Non-interactive Folding Scheme。
与基于SANRK的IVC方案类似,Prover采用augmented函数 F ′ F' F′,其中每个step i i i包含:
- 当前step对 F ′ F' F′函数的调用:对应committed relaxed R1CS instance u i u_i ui,其中包含了 z i z_i zi, F ′ F' F′用于计算 z i + 1 = F ( z i ) z_{i+1}=F(z_i) zi+1=F(zi)。
- 之前step的 F ′ F' F′函数的调用:对应committed relaxed R1CS instance U i U_i Ui,表示之前的 1 , ⋯ , i − 1 1,\cdots, i-1 1,⋯,i−1次 F ′ F' F′调用的正确执行。
F ′ F' F′中包含2个任务:
- 1)执行当前step的增量计算:即instance u i u_i ui中包含了 z i z_i zi, F ′ F' F′用于计算 z i + 1 = F ( z i ) z_{i+1}=F(z_i) zi+1=F(zi)。
- 2)触发folding scheme的Verifier:将committed relaxed R1CS instance u i u_i ui和 U i U_i Ui合并一个instance U i + 1 U_{i+1} Ui+1。
IVC Prover:
- 计算新的instance
u
i
+
1
u_{i+1}
ui+1:以保证第
i
+
1
i+1
i+1次调用
F
′
F'
F′的正确执行,从而确保
z
i
+
1
=
F
(
z
i
)
z_{i+1}=F(z_i)
zi+1=F(zi) 且
U
i
+
1
U_{i+1}
Ui+1为
u
i
u_i
ui和
U
i
U_i
Ui的folding结果。
此时:- U i + 1 U_{i+1} Ui+1:表示第 1 , ⋯ , i 1,\cdots,i 1,⋯,i次调用 F ′ F' F′的正确执行。将 F ′ F' F′在step i i i中输出的instance U i + 1 U_{i+1} Ui+1 称为running instance。
- u i + 1 u_{i+1} ui+1:表示第 i + 1 i+1 i+1次调用 F ′ F' F′的正确执行。instance u i u_i ui中包含了 z i z_i zi, F ′ F' F′用于计算 z i + 1 = F ( z i ) z_{i+1}=F(z_i) zi+1=F(zi)。
简化表示为:


与Halo的IVC方案类似,只是其中:
-
V
V
V:为non-interactive folding scheme的Verifier,而不是accumulator。
具有最低的recursion开销(即Verifier circuit size):约1万个gate。 - u i u_i ui:为previous step的witness的commitment承诺值。对应step instance。
- U i U_i Ui:为”running witness“ 和 "running error-term"的commitment承诺值。对应running instance。
相应的Recursive proof为: ( u n , U n ) (u_n, U_n) (un,Un) + 相应的witness,由2部分组成:
- 1)最后一个step的2个承诺值 ( u n , U n ) (u_n, U_n) (un,Un),分别对应step instance和running instance。
- 2)对应最后一个step的witness
(
w
n
,
W
n
)
(w_n,W_n)
(wn,Wn),分别对应step instance的witness和running instance的witness。
该witness与step size呈线性关系。

Nova再次将step instance和running instance再fold为一个: - ( U , W ) (\mathbf{U,W}) (U,W):其中 U = ( W ˉ , E ˉ , u , x ) , W = ( W , E ) \mathbf{U}=(\bar{W},\bar{E},u,x), \mathbf{W}=(W,E) U=(Wˉ,Eˉ,u,x),W=(W,E)。
这样可将Recursive proof size减半,但proof size仍为 O ( ∣ C ∣ ) O(|C|) O(∣C∣)个field elements。
不过,直观方案是:
- 可引入某zkSNARK方案来证明knowledge of satisfying ( U , W ) (\mathbf{U,W}) (U,W),从而可提供额外的succinctness和zero-knowledge属性。但是相应的证明开销将是昂贵的。
针对:
- π = ( U , W ) \pi=(\mathbf{U,W}) π=(U,W):其中 U = ( W ˉ , E ˉ , u , x ) , W = ( W , E ) \mathbf{U}=(\bar{W},\bar{E},u,x), \mathbf{W}=(W,E) U=(Wˉ,Eˉ,u,x),W=(W,E)。
Nova的压缩proof size的方案为:
- 1)将 ( W ˉ , E ˉ ) (\bar{W},\bar{E}) (Wˉ,Eˉ)看成是multilinear多项式的承诺值。
- 2)使用基于multilinear多项式的SNARK方案,如Nova中使用Spartan [S19]来证明,对于所承诺的多项式,如下R1CS关系成立:
A ⋅ z ∘ B ⋅ z = u ⋅ C ⋅ z + E A\cdot z\circ B\cdot z = u\cdot C\cdot z + E A⋅z∘B⋅z=u⋅C⋅z+E,其中 Z = ( W , x , u ) Z=(W,x,u) Z=(W,x,u)
从而可将proof size由
O
(
∣
C
∣
)
O(|C|)
O(∣C∣)个field elements,reduce为,
O
(
log
∣
C
∣
)
O(\log{|C|})
O(log∣C∣)个group elements,从而实现了指数级的压缩改进。
也可将
(
W
ˉ
,
E
ˉ
)
(\bar{W},\bar{E})
(Wˉ,Eˉ)看成是向量承诺值,也可使用其它证明系统(如Plonk、Marlin等等)。
4.4 使用Nova来证明机器执行

当将Nova用于证明机器执行时:
-
C
C
C中编码了VM的某个step,该step可执行所支持的任意指令:
- ADD、MUL、KECCAK256、SLOAD、SSTORE、ECADD、ECMUL、ECPAIRING等等。
- 这样的缺陷之一是, C C Csize与所支持的指令数呈比例: ∣ C ∣ ≥ ∣ C A D D ∣ + ∣ C M U L ∣ + ∣ C K E C C A K 256 + ∣ C S L O A D ∣ + ⋯ |C|\geq |C_{ADD}|+|C_{MUL}|+|C_{KECCAK256}+|C_{SLOAD}|+\cdots ∣C∣≥∣CADD∣+∣CMUL∣+∣CKECCAK256+∣CSLOAD∣+⋯
为证明某个step,相应Prover的开销为:
- 至少 O ∣ C ∣ O|C| O∣C∣次crypto运算
为此,要求 C C C尽可能小,即实现minimal VM,但是让其尽可能小无法解决实际应用需要,因为某些实际程序,过小的VM意味着需增加递归调用次数。
4.5 使用SuperNova来证明机器执行
4.5.1 Non-uniform IVC
已知:
- l + 1 l+1 l+1non-deterministic函数: C 1 , C 2 , ⋯ , C l C_1,C_2,\cdots,C_l C1,C2,⋯,Cl和 ϕ \phi ϕ。其中 ϕ \phi ϕ函数用于帮助选择IVC中每个step所执行的指令。
- 初始输入值 z 0 z_0 z0
证明:
- z n z_n zn为运行 C j C_j Cj n n n次的结果,其中在step i i i,有 j = ϕ ( w i − 1 , z i − 1 ) j=\phi(w_{i-1},z_{i-1}) j=ϕ(wi−1,zi−1)。【即 ϕ \phi ϕ函数会将witness w i − 1 w_{i-1} wi−1和input z i − 1 z_{i-1} zi−1,映射为 1 1 1到 l l l之间的某个值。】

4.5.2 将Nova看成是单个指令的Non-uniform IVC
将Nova看成是单个指令的Non-uniform IVC:【即
ϕ
\phi
ϕ函数确定性的返回1,可忽略。】

4.5.3 将SuperNova看成是对多个指令的Non-uniform IVC
将SuperNova看成是对多个指令的Non-uniform IVC,其简化版表示为:

其中:
- p c i pc_i pci为第 i i i个step所执行的函数的index,其结果值为 1 1 1到 l l l中某个值。
”将SuperNova看成是对多个指令的Non-uniform IVC“ 与 ”将Nova看成是单个指令的Non-uniform IVC“ 的关键不同之处在于:
- non-interactive folding scheme中的Verifier
N
I
F
S
.
V
NIFS.V
NIFS.V:
- 从多个Running instance选中一个 U i , p c i U_{i,pc_i} Ui,pci与 u i u_i ui合并,即只更新一个running instance。
”将SuperNova看成是对多个指令的Non-uniform IVC“时,每个step所执行的指令可能不同,具体在某个step执行哪个指令由 φ \varphi φ函数以及 witness w i − 1 w_{i-1} wi−1和input z i − 1 z_{i-1} zi−1 共同决定。
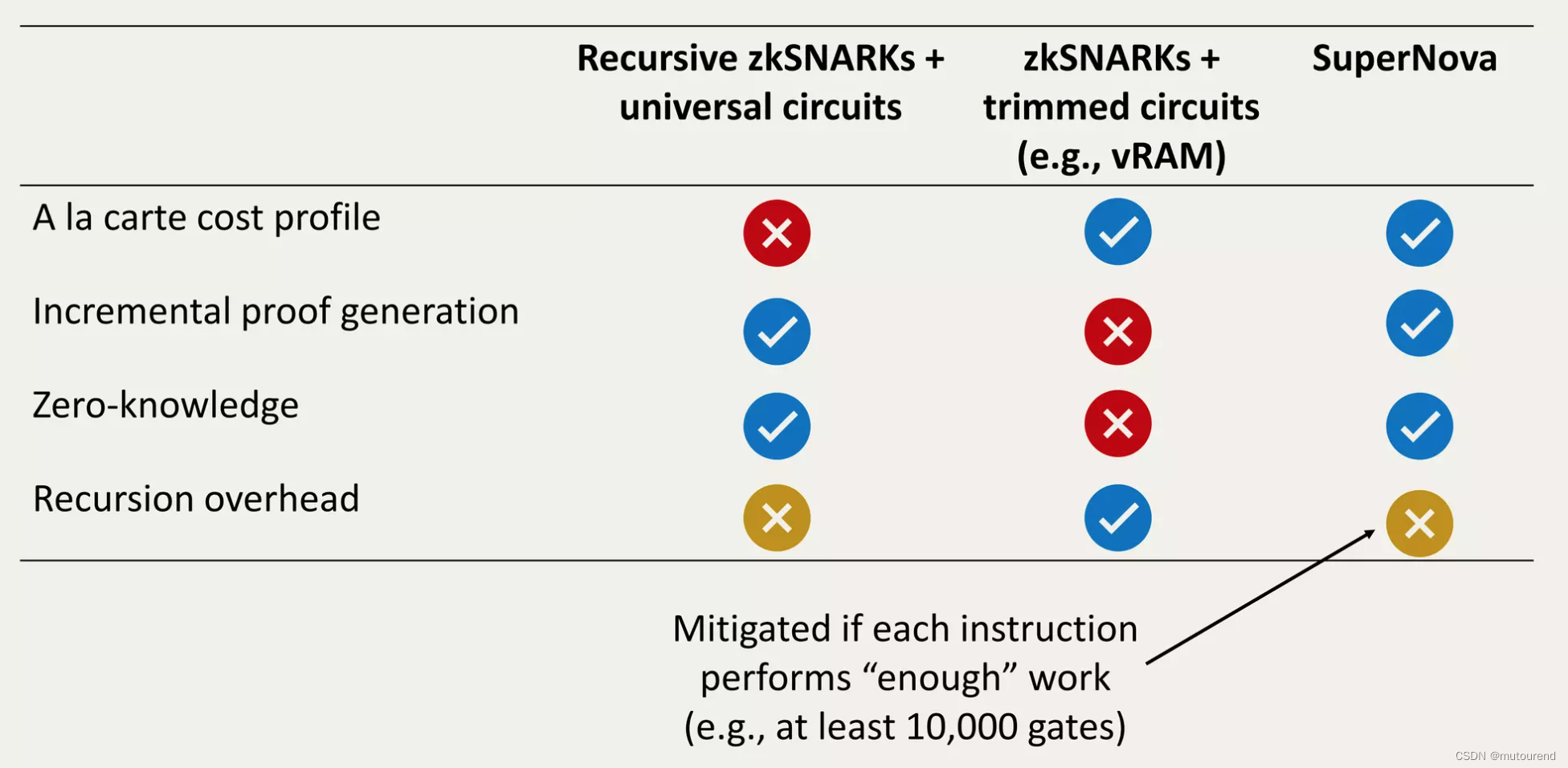
4.5.3 SuperNova性能对比
5. 小结
SuperNova为一种新的证明系统,其具有fast prover和small proof:
- 提供了”a la carte(点菜)“ cost profile:仅pay for what is executed。
- 引入了folding scheme等新技术
- 通过Spartan利用了如linear-time sum-checks等最佳技术。
相比同类方案,SuperNova具有诸多优势,为构建基于proof的trustless service提供了新的选型。
HyperNova:
- 支持对customizable constraint system(CCS)的证明。






![深度学习 - 52.推荐场景的多样性与 MMR [Maximal Marginal Relevance] 简介与 Python 实现](https://img-blog.csdnimg.cn/5ff39b73dc78496f8559afba2b144fe2.png)