文章目录
- 前言
- 一、思想
- 二、相关题目讲解
- 1.长度最小的子数组(leetcode 209.)
- 2.水果成篮(leetcode 904.)
- 3.最小覆盖子串(leetcode 76.)
- 三、 模拟行为
- 螺旋矩阵II(leetcode.59)
- leetcode 54.螺旋矩阵
- 剑指Offer 29. 顺时针打印矩阵
- 总结
前言
滑动窗口的精妙之处在于根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将O(n2 )的暴力解法降为O(n)。主要要理解滑动窗口如何移动窗口起始位置,达到动态更新窗口大小的,从而得出长度最小的符合题目条件的长度。
一、思想
那么滑动窗口是如何用一个for循环来完成整个操作的呢?
首先思考用一个for循环,那么应该表示滑动窗口的起始位置,还是终止位置。
如果只用一个for循环来控制滑动窗口的起始位置,那么剩下的终止位置如何遍历?这就又回到了暴力解法。
所以只用一个for循环的话,那么这个循环的索引,一定是表示滑动窗口的终止位置。那么滑动窗口的起始位置如何操作移动呢?
实现滑动窗口,主要确定如下三点:
(1) 窗口内是什么?
(2) 如何移动窗口的起始位置?
(3) 如何移动窗口的结束位置?
窗口就是满足长度最小的符合题目条件的连续子数组。
窗口的起始位置如何移动:如果当前窗口的值大于s了,窗口就要向前移动了(也就是该缩小了)。
窗口的结束位置如何移动:窗口的结束位置就是遍历数组的指针,也就是for循环里的索引。
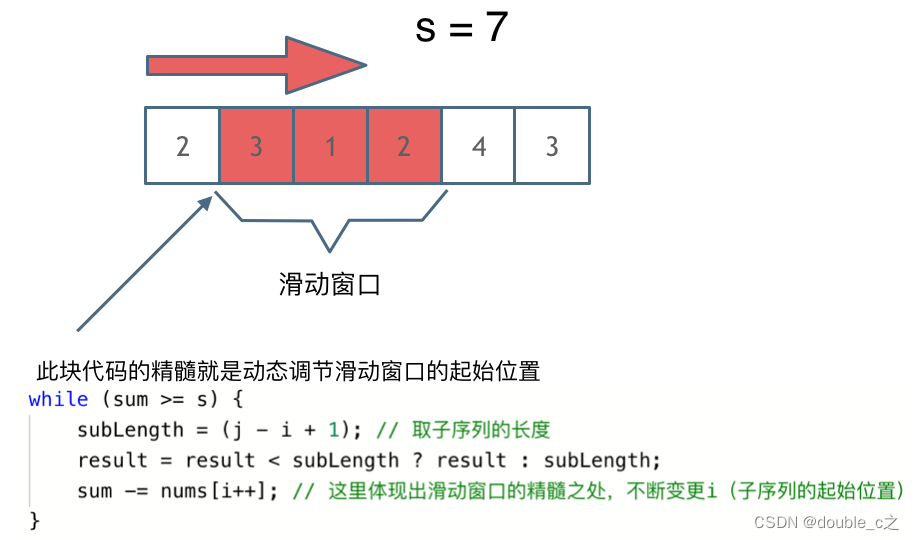
通过这个图例可以体会到滑动窗口的精妙之处在于根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将O(n2 )暴力解法降为O(n)。
二、相关题目讲解
1.长度最小的子数组(leetcode 209.)
代码如下(示例):
class Solution:
def minSubArrayLen(self, target: int, nums: List[int]) -> int:
l=len(nums)
left=0
right=0
min_len=float('inf')#正无穷
cur_sum=0
for right in range(0,l):
cur_sum += nums[right]
while cur_sum >= target: # 当前累加值大于目标值
min_len = min(min_len, right - left + 1)
cur_sum -= nums[left]
left += 1 #移动滑动窗口起始位置
right += 1 #移动滑动窗口结束位置
return min_len if min_len != float('inf') else 0
时间复杂度是O(n),有同学可能会问为什么不是O(n2 )呢,因为一个for循环下,虽然里面还放一个while循环,但是主要看每一个元素被操作的次数,每个元素在滑动窗后进来操作一次,出去操作一次,每个元素都是被操作两次,所以时间复杂度是 2 × n 也依旧是O(n)。
2.水果成篮(leetcode 904.)
代码如下(示例):
class Solution:
def totalFruit(self, fruits: List[int]) -> int:
l=len(fruits)
left=0
res=0
classMap=defaultdict(int)#
classCnt=0
for right in range(0,l):
if classMap[fruits[right]]==0:
classCnt+=1
classMap[fruits[right]]+=1
while classCnt>2:
if classMap[fruits[left]]==1:
classCnt-=1
classMap[fruits[left]]-=1
left+=1
#一旦满足条件,更新结果
res = max(res, right - left + 1)
return res
本题区别于76题,这道题求的是最大滑窗,最大滑窗模版:给定数组 nums,定义滑窗的左右边界 left, right,求满足某个条件的滑窗的最大长度。关键的区别在于,最大滑窗是在迭代右移右边界的过程中更新结果,而最小滑窗是在迭代右移左边界的过程中更新结果。因此虽然都是滑窗,但是两者的模板和对应的贪心思路并不一样。
while right < len(nums):#滑动窗口结束位置的遍历
判断[left, right]是否满足条件
while 不满足条件:
left += 1 (最保守的压缩i,一旦满足条件了就退出压缩i的过程,使得滑窗尽可能的大)
不断更新结果(注意在while外更新!)
right+= 1
3.最小覆盖子串(leetcode 76.)
class Solution:
def minWindow(self, s: str, t: str) -> str:
from collections import Counter#快速计数
template_dict=Counter(t)#统计目标字符串里各字符的个数
window_dict={}#定义了一个滑动窗口字典
for each_key in template_dict:#对于目标字符串的每个字符
if each_key not in window_dict:#如果不在滑动窗口里
window_dict[each_key]=0#就赋值为零
def isContains(cur_dict,tmp_dict):
for each_key in tmp_dict:
if cur_dict[each_key]<tmp_dict[each_key]:#如果滑动窗口
return False
return True
start=0#定义滑动窗口起始位置
min_len=float('inf')#定义滑动窗口长度
res=''
for end in range(len(s)):#滑动窗口结束位置的遍历
if s[end] in template_dict:#如果字符串的字符出现在目标字符串里
window_dict[s[end]]+=1#滑动窗口对应字符附值+1
while isContains(window_dict,template_dict):#滑动窗口满足目标要求
if min_len>end-start+1
min_len=end-start+1
res=s[start:end+1]
if s[start] in window_dict:
window_dict[s[start]]-=1
start+=1
return res
本题是最小滑窗思路,最小滑窗模板:给定数组 nums,定义滑窗的左右边界 left, right,求满足某个条件的滑窗的最小长度。滑动窗口简单说就是右指针先出发,左指针视情况追赶右指针。因此,右指针最多遍历一遍数组,左指针也最多遍历一次数组,时间复杂度不超过O(2N)。接下来,如何判断滑动窗口内是否满足题设条件,有两种选择:(1) 要么你遍历这个滑窗,通过遍历来断滑窗是否满足需要O(N), 那么总的时间就退化为O(N2), (2) 要么你选择字典,用空间换时间,那么判断划窗是否满足条件则需要 O(1),总时间为O(N).
while right < len(nums):
判断[eft, right]是否满足条件
while 满足条件:
不断更新结果(注意在while内更新!)
left += 1 (最大程度的压缩i,使得滑窗尽可能的小)
right += 1
三、 模拟行为
螺旋矩阵II(leetcode.59)
这道题在面试中出现频率较高,不涉及算法,就是模拟过程,考察候选人的代码能力
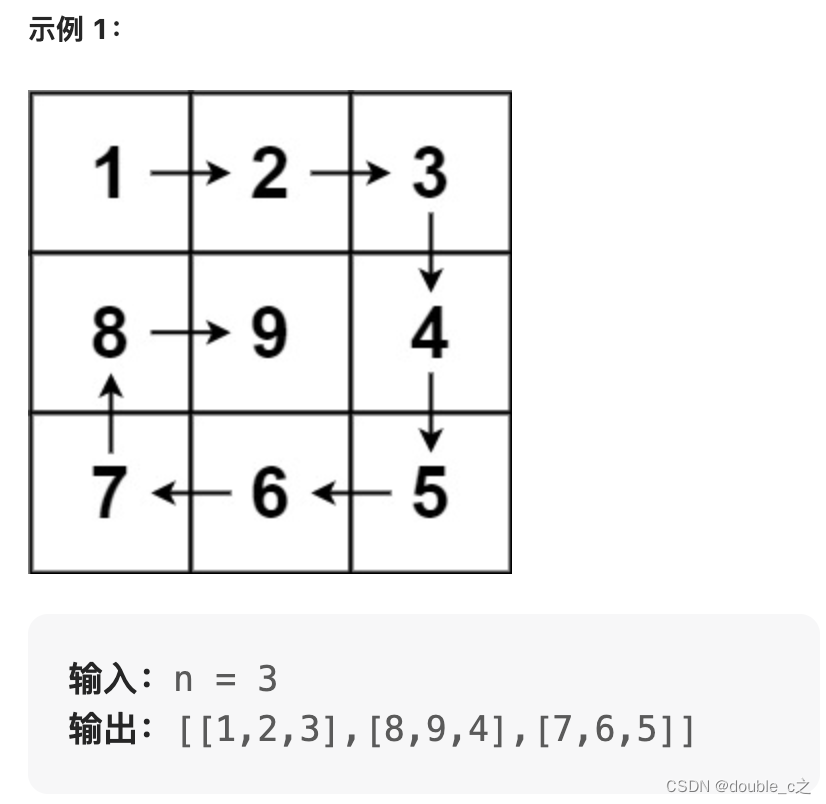
模拟顺时针画矩阵的过程:
上行从左到右
右列从上到下
下行从右到左
左列从下到上
由外向内一圈一圈这么画下去。
发现边界条件非常多,在一个循环中,如此多的边界条件,如果不按固定规则来遍历,就容易陷入循环陷阱。
思路:
startx=0,starty=0
offset=1
count=1
while(n/2){
for(j=starty;j<n-offset;j++) #从左到右
nums[startx][j]=count++;
for(i=startx;i<n-offset;i++)#从上到下
nums[i][j]=count++;
for(j=n-offset;j>s;j--)#从右到左
nums[i][j]=count++;
for( ;i>startx;i--)
nums[i][j]=count++;
具体实现代码:
class Solution:
def generateMatrix(self, n: int) -> List[List[int]]:
nums = [[0] * n for _ in range(n)]
startx, starty = 0, 0 # 起始点
loop, mid = n // 2, n // 2 # 迭代次数、n为奇数时,矩阵的中心点
count = 1 # 计数
for offset in range(1, loop + 1) : # 每循环一层偏移量加1,偏移量从1开始
for i in range(starty, n - offset) : # 从左至右,左闭右开
nums[startx][i] = count
count += 1
for i in range(startx, n - offset) : # 从上至下
nums[i][n - offset] = count
count += 1
for i in range(n - offset, starty, -1) : # 从右至左
nums[n - offset][i] = count
count += 1
for i in range(n - offset, startx, -1) : # 从下至上
nums[i][starty] = count
count += 1
startx += 1 # 更新起始点
starty += 1
if n % 2 != 0 : # n为奇数时,填充中心点
nums[mid][mid] = count
return nums
复杂度分析:时间复杂度:O(n2),其中 n是给定的正整数。矩阵的大小是 nxn,需要填入矩阵中的每个元素。
空间复杂度:O(1)。除了返回的矩阵以外,空间复杂度是常数。
leetcode 54.螺旋矩阵
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
if not matrix or not matrix[0]:
return list()
rows, columns = len(matrix), len(matrix[0])
order = list()
left, right, top, bottom = 0, columns - 1, 0, rows - 1
while left <= right and top <= bottom:
for column in range(left, right + 1):
order.append(matrix[top][column])
for row in range(top + 1, bottom + 1):
order.append(matrix[row][right])
if left < right and top < bottom:
for column in range(right - 1, left, -1):
order.append(matrix[bottom][column])
for row in range(bottom, top, -1):
order.append(matrix[row][left])
left, right, top, bottom = left + 1, right - 1, top + 1, bottom - 1
return order
时间复杂度:O(mn),其中 m 和 n分别是输入矩阵的行数和列数。矩阵中的每个元素都要被访问一次。
空间复杂度:O(1)。除了输出数组以外,空间复杂度是常数。
剑指Offer 29. 顺时针打印矩阵
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
if not matrix or not matrix[0]:
return list()
rows, columns = len(matrix), len(matrix[0])
order = list()
left, right, top, bottom = 0, columns - 1, 0, rows - 1
while left <= right and top <= bottom:
for column in range(left, right + 1):
order.append(matrix[top][column])
for row in range(top + 1, bottom + 1):
order.append(matrix[row][right])
if left < right and top < bottom:
for column in range(right - 1, left, -1):
order.append(matrix[bottom][column])
for row in range(bottom, top, -1):
order.append(matrix[row][left])
left, right, top, bottom = left + 1, right - 1, top + 1, bottom - 1
return order
同样的解题思路,时间复杂度:O(mn),其中 m 和 n分别是输入矩阵的行数和列数。矩阵中的每个元素都要被访问一次。
空间复杂度:O(1)。除了输出数组以外,空间复杂度是常数。
总结
滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。最容易想到的暴力解法,步骤是一个for循环控制滑动窗口的起始位置,另一个for循环控制滑动窗口的终止位置,用两个for循环完成了一个不断搜索区间的过程,时间复杂度是O(n2 )。而滑动窗口的精妙之处在于,用一个for循环完成区间的搜索,时间复杂度是O(n)。


![深度学习 - 52.推荐场景的多样性与 MMR [Maximal Marginal Relevance] 简介与 Python 实现](https://img-blog.csdnimg.cn/5ff39b73dc78496f8559afba2b144fe2.png)



![C# webapi接口传输byte[]数据,报错:415 Unsupported Media Type](https://img-blog.csdnimg.cn/3ac96157a7404d9fb43a65e18e4390e3.png)