分数 25
全屏浏览题目
切换布局
作者 CHEN, Yue
单位 浙江大学
Given a syntax tree (binary), you are supposed to output the corresponding infix expression, with parentheses reflecting the precedences of the operators.
Input Specification:
Each input file contains one test case. For each case, the first line gives a positive integer N (≤ 20) which is the total number of nodes in the syntax tree. Then N lines follow, each gives the information of a node (the i-th line corresponds to the i-th node) in the format:
data left_child right_child
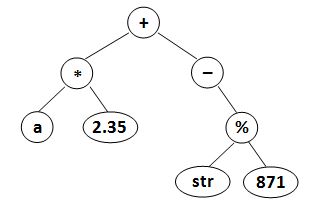
where data is a string of no more than 10 characters, left_child and right_child are the indices of this node's left and right children, respectively. The nodes are indexed from 1 to N. The NULL link is represented by −1. The figures 1 and 2 correspond to the samples 1 and 2, respectively.
|
|
|
|---|---|
| Figure 1 | Figure 2 |
Output Specification:
For each case, print in a line the infix expression, with parentheses reflecting the precedences of the operators. Note that there must be no extra parentheses for the final expression, as is shown by the samples. There must be no space between any symbols.
Sample Input 1:
8
* 8 7
a -1 -1
* 4 1
+ 2 5
b -1 -1
d -1 -1
- -1 6
c -1 -1
Sample Output 1:
(a+b)*(c*(-d))
Sample Input 2:
8
2.35 -1 -1
* 6 1
- -1 4
% 7 8
+ 2 3
a -1 -1
str -1 -1
871 -1 -1
Sample Output 2:
(a*2.35)+(-(str%871))
代码长度限制
16 KB
时间限制
400 ms
内存限制
64 MB
#include<bits/stdc++.h>
using namespace std;
const int N=25;
int n;
string node[N];//记录结点的符号
int l[N],r[N],exist[N];//记录左右子树的结点号,和出现过的左右孩子
bool isleaf(int u){//判断是否是叶子结点
if(l[u]==-1&&r[u]==-1)return true;
else return false;
}
string inorder(int u){
string lchild,rchild;
if(l[u]!=-1){//有左子树
lchild=inorder(l[u]);//记录左子树
if(!isleaf(l[u]))lchild="("+lchild+")";//若左子树不是叶结点则加上括号
}
if(r[u]!=-1){//有右子树
rchild=inorder(r[u]);//记录右子树
if(!isleaf(r[u]))rchild="("+rchild+")";//若右子树不是叶结点则加上括号
}
return lchild+node[u]+rchild;//输出左子树+中间结点+右子树
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){//输入
cin>>node[i]>>l[i]>>r[i];
if(l[i]>0)exist[l[i]]=1;//记录出现过的左孩子结点
if(r[i]>0)exist[r[i]]=1;//记录出现过的右孩子结点
}
int root;
for(int i=1;i<=n;i++)if(!exist[i])root=i;//没出现的结点就是根结点
cout<<inorder(root)<<endl;
return 0;
}