目录

1.第一题

2.第二题

3.第三题

---

1.第一题

160. 相交链表 - 力扣（LeetCode）

思路分析：

看链表相不相交，是看链表的地址。把两个链表的地址一一比对，如有有相同的地址，那么相交，如果各不相同，那么肯定不相交。

但是如果要一一比对的话，时间复杂度是N^2,效果太差了。时间复杂度是N^2的原因是，有可能两个链表的长度不一样。假如两个链表的长度一样的话，就不需要一一比对了，只需要各自位置上的节点对比就行。这样的话时间复杂度是N。

 

 那么现在只要人让长的先走，走到和短的一样长，之后，长的短的一起走。这个时候再去对比地址，相同返回相交的节点，不同返回NULL

参考代码：

struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) 
{
    struct ListNode * curA = headA;
    struct ListNode * curB = headB;
    int lenA = 0;
    int lenB = 0;
    
    //找尾
    while(curA->next)
    {
        lenA++;
        curA =curA->next;
    }
     while(curB->next)
    {
        lenB++;
        curB =curB->next;
    }
    //尾节点不相等就相交
    if(curA!=curB)
        return NULL;
    
    int gap = abs(lenA-lenB);
    struct ListNode* longlist = headA;
    struct ListNode* shortlist = headB;
    if(lenB>lenA)
    {
        longlist=headB;
        shortlist=headA;
    }

    //长先走差距步
    while(gap--)
    {
        longlist = longlist->next;
    }

    //同时走，找交点
    while(longlist!=shortlist)
    {
        longlist =longlist->next;
        shortlist =shortlist->next;
    }
    return longlist;

}

2.第二题

141. 环形链表 - 力扣（LeetCode）

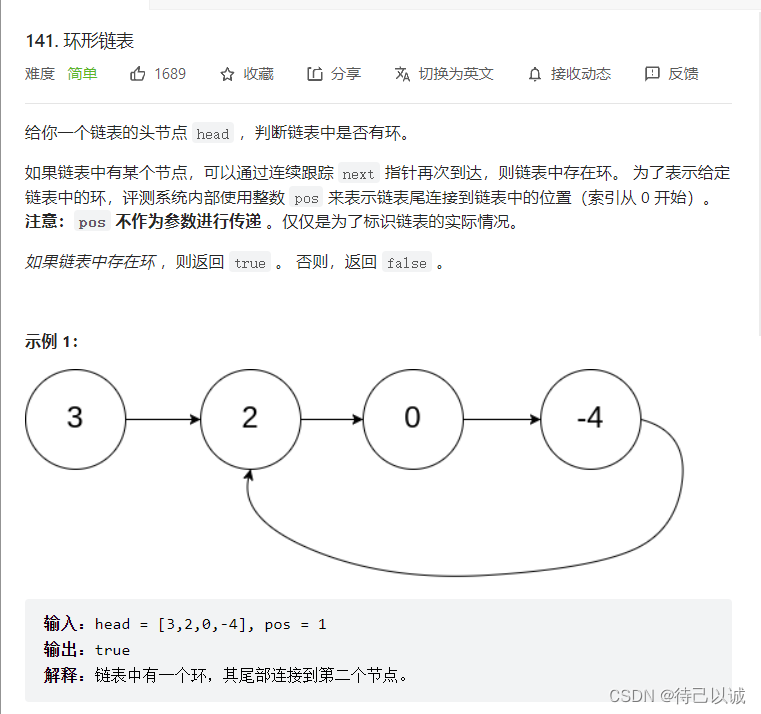
 思路分析：

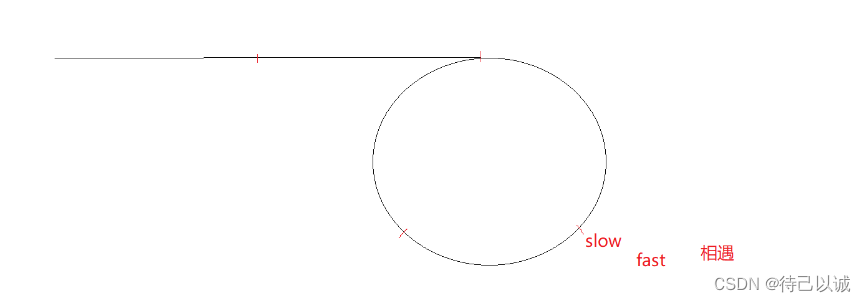
利用双指针中的快慢指针，两个指针一个走一步，一个走两步，如果没有环的话，就会走完整个链表，如果有环的话，那么两个指针都会进入到环里面，在环里面的话，就会演变成一个追击的问题，快的总会追上慢的。

由于快的走两步，慢的走一步，那么快的相对比慢的速度就是1步，那么快的肯定会和慢的相遇，那么就能追上慢的。

 

 （图中为抽象的链表）

参考代码：

bool hasCycle(struct ListNode *head)
{
    struct ListNode* fast = head;
    struct ListNode* slow = head;
    while(fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
        if(fast == slow)
        return fast;
    }
    return NULL;
}

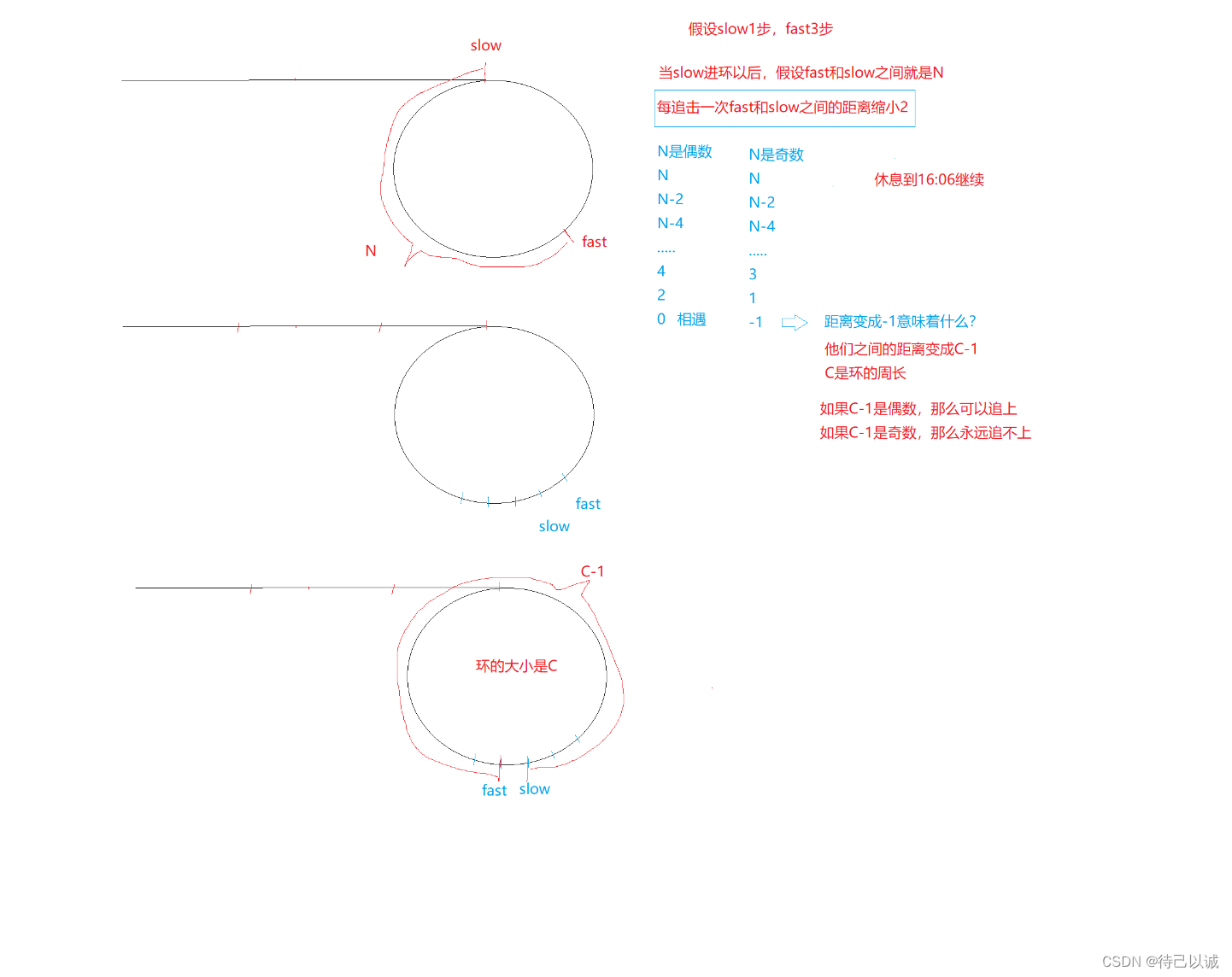
PS:思考，为什么设计成快的走2步？

为什么步设计成快的走3，4，5，6……步呢？

其实只要是有环的话，快的和慢的都会进入环中，那么假如快的走3步的话，那么和慢的的速度差就是2步，那么就有可能会越过慢的，只要当慢的和快的之间的节点数只差是奇数的话，那么快的总是会越过慢的

 

3.第三题

142. 环形链表 II - 力扣（LeetCode）

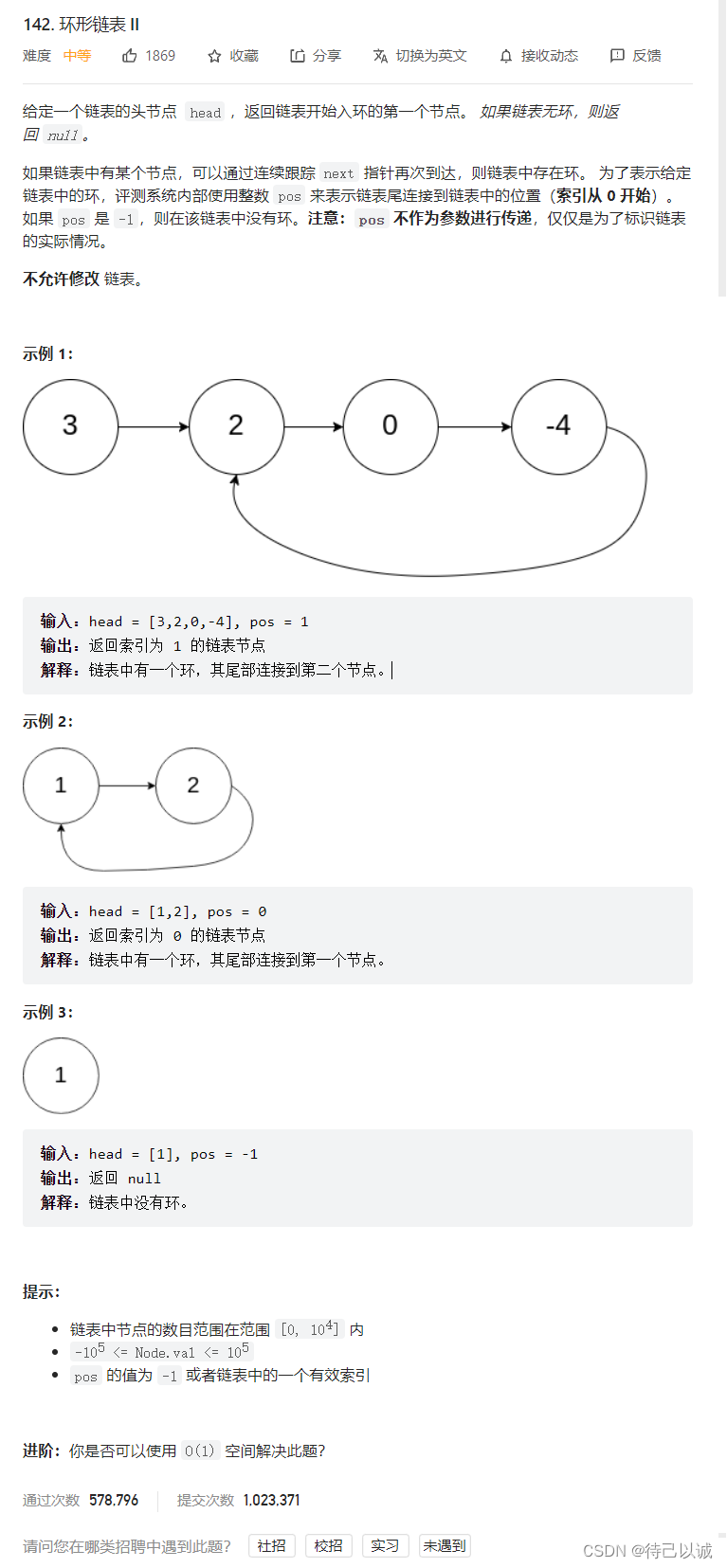
 思路分析:

现在要求的是入环点，

先上结论：从头节点走到入环点的距离就是相交点走到入环点的距离。

前提条件：相交点必须是快慢指针的相交点（也就是第二题中的），快指针一次走两步，满指针一次走一步。那么到相交的时候快指针走的距离就是慢指针走的距离的两倍。

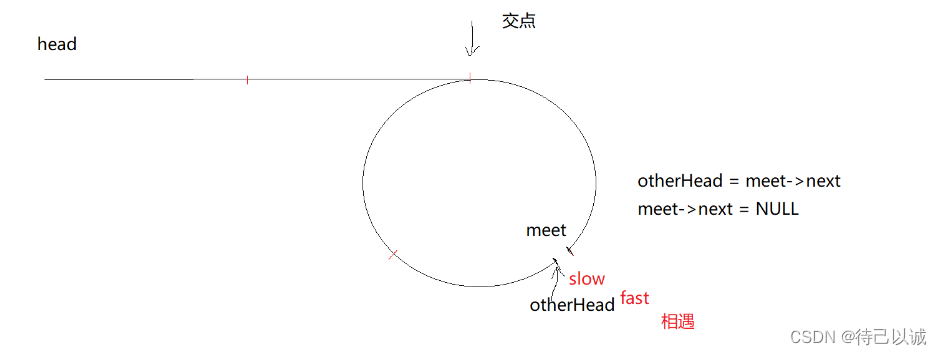
具体的结论分析看下图：

 第二种思路：

将乡遇点meet置空，然后otherhead作为第二个头节点，那么这个问题可以看成是两个链表的相交问题，相交点就是之前的入环点。 

第一种思路的参考代码：

struct ListNode *detectCycle(struct ListNode *head) 
{
    struct ListNode* fast = head;
    struct ListNode* slow = head;
    while(fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
        if(fast == slow)
        {
            struct ListNode * meet = slow;
            while(head != meet)
            {
                head=head->next;
                meet=meet->next;
            }
            return meet;
        }
       
    }
    return NULL;
}