定点数

• 编程时需要确定小数点位置
• 难以表示两个大小相差较大的数
• 存储空间利用率低

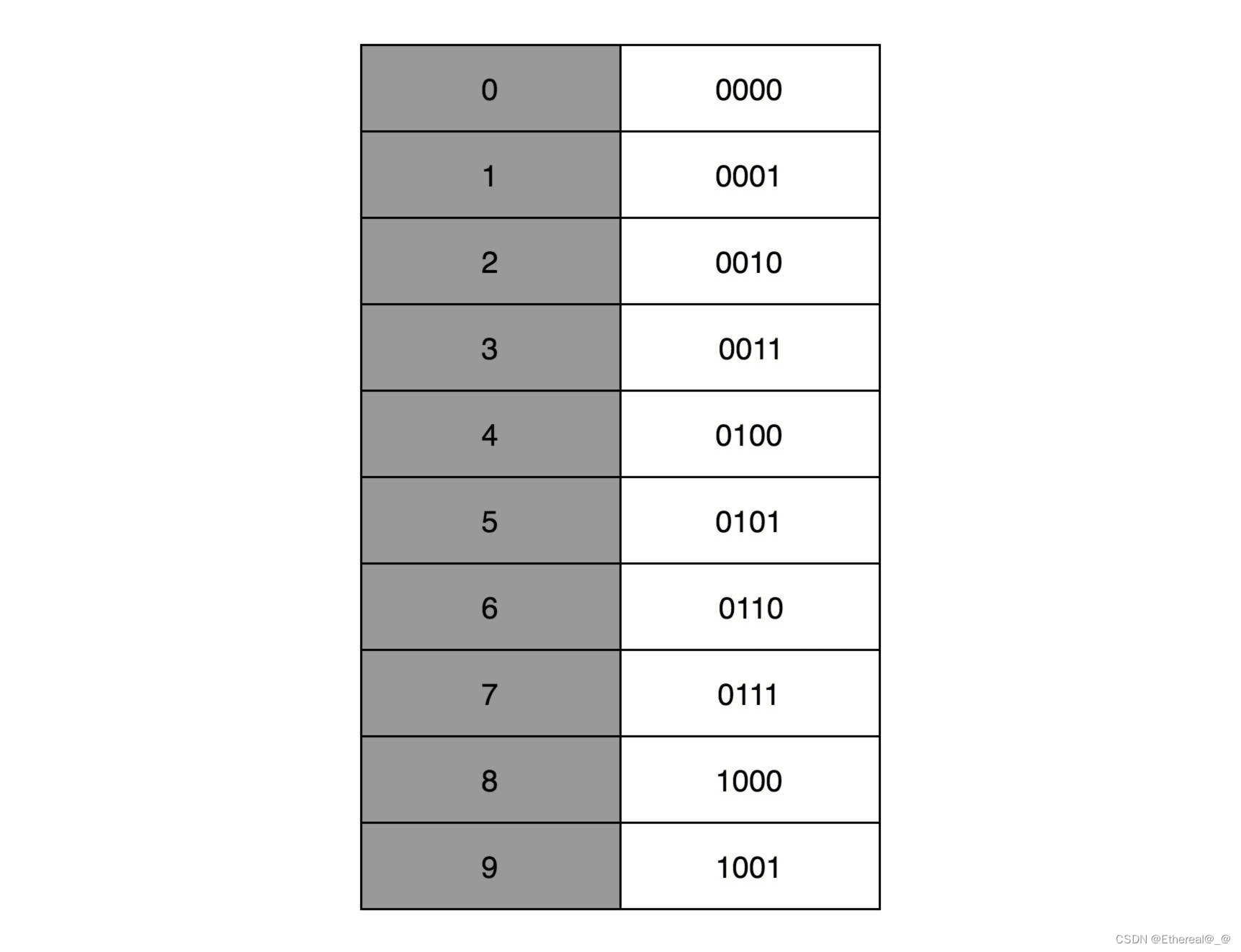
这种用二进制来表示十进制的编码方式，叫作BCD 编码（Binary-Coded Decimal）。

浮点数

• 小数点的位置可以左右移动的数

规格化浮点数:

• IEEE 754规格化的尾数形式为：1.x…x。

浮点数的不精确性：

>>> 0.3 + 0.6
0.8999999999999999

浮点数的加法和精度损失：

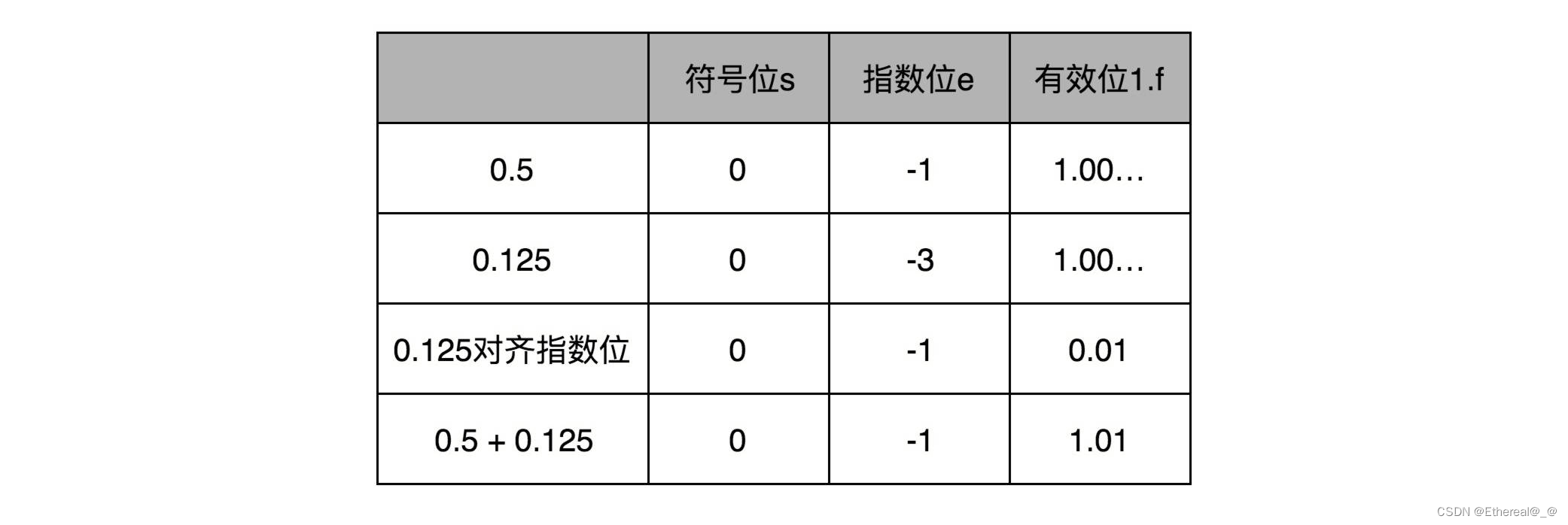
其中指数位较小的数，需要将有效位进行右移（小数点不动，数右移），在右移的过程中，最右侧的有效位就可能被丢弃掉。这会导致对应的指数位较小的数，在加法发生之前，就丢失精度。两个相加数的指数位差的越大，位移的位数越大，可能丢失的精度也就越大。

---

无符号数

加法运算：

• 1+1 = 0（有进位）

减法运算：

• 0-1 = 1（有借位）

乘法运算：

• 每乘以2，相对于被乘数向左移动一位，最右边补0
• 乘法实际上是移位和加法的运算。

除法运算：

• 每除以2，相当于被乘数向右移动1位，最左边补0
• 除法实际上是移位和减法的运算。

---

有符号数

• 用最高位表示符号，其余是数值
• 最高位是0：表示正数；最高位是1：表示负数

符号数的表示方法：
原码：最高位为符号位，其余为真值部分。符号位+【绝对值】

• 优点：真值和其原码之间的对应关系简单，容易理解。
• 缺点：计算机中用原码进行加减运算比较困难；0的表示不唯一。

0的原码表示不唯一：

• +0 = 0000 0000
• -0 = 1000 0000

反码：正数的反码与原码相同，负数的反码则是在原码的基础上符号位不变，数值部分按位取反。<br /

X = -52 = -011 0100
[X]原 = 10110100
[X]反 = 11001011

0的反码也不是唯一的：

[+0]反 = [+0]原 = 0000 0000
[-0]原 = 1000 0000
[-0]反 = 1111
1111

补码：若 X > 0，则[X]补 = [X]反 = [X]原；若X < 0，则[X]补 = [X]反+1。

X = -52 = -011 0100
[X]原 = 10110100
[X]反 = 11001011
[X]补 = [X]反 + 1 = 1100 1100
[X]原 也等于 [[X]补]补

0的补码：

[+0]补 = [+0]原 = 0000 0000
[-0]补 = [-0]反+1 = 1111 1111 + 1 = 10000 0000
对于8位有效字长，进位 (第9位) 被舍掉，我们看到的就是8个0，这样一来，就和+0的补码一样了。

所以，补码解决了 0 的表示不唯一的问题。


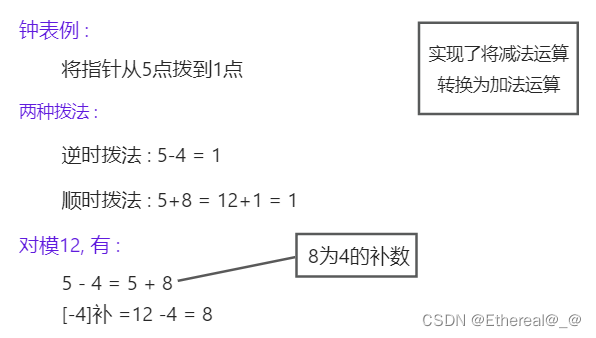
除此之外，补码也实现了将减法运算转换为加法运算。

注：我们在实际编程时，负数可用“-”表示。由编译系统将其转换为补码。
例如：-3 编译后的值为 FDH，1111 1101B就是-3的补码。

补码的算术运算：

• [X + Y]补 = [X]补 + [Y]补
• [X - Y]补 = [X + (-Y)]补 = [X]补 + [-Y]补

---

特殊数1000 0000

对于无符号数：

• 1000 0000 B = 128

在原码中的定义为：

• 1000 0000 B = -0

在反码中的定义为：

• 1000 0000 B = -127

在补码中的定义为：

• 1000 0000 B = -128

计算机能够表示的数是有限的，例如你的计算机是64位，一次最多只能处理64位长的数据。当运算结果超出了计算机所能表示的范围的时候（例如64位机），就会产生溢出。

---

无符号数的表示范围

无符号数的表示范围：

• 0 <= X <= 2n-1，n表示字长

无符号数加减运算溢出的判断方法：

• 当最高位向更高位有进位（或借位）时产生溢出。
• 例如，对于8位机来讲，8个1再加一，溢出位超出了有效字长，在有效字长范围内，结果为0（出错）。最高的进位1会放在一个特殊的位置。

有符号数的表示范围

注：n表示字长
原码和反码：

• -(2n-1-1) <= X <= 2n-1-1

补码：

• 2n-1<= X <= 2n-1-1

对于8位2进制数：

• 原码：-127 ~ +127
• 反码：-127 ~ +127
• 补码：-128 ~ +127

有符号数加减运算溢出的判断方法：

因为无符号数和有符号数的表示范围不一样，所以判断是否溢出的方法也不一样。
对于有符号数, 判断是否溢出,要用双位。

• 最高位进位状态 异或 次高位进位状态 = 1, 则结果溢出。
• 异或: 相同为0, 相异为1。

乘法运算不存在溢出问题, 而除法运算溢出时, 会产生 “除数为0” 中断.

注: 计算机中的符号数默认以补码形式表示。
只有原码的数值部分是真值。
反码和补码的数值部分都不是真值。