维纳过程和伊藤引理

news2024/12/24 9:06:15

一、马尔可夫过程（Markov）

1. 基本概念

2. 具体使用

二、维纳过程

1. 基本概念

2. 具体使用

三、广义维纳过程

1. 漂移率和方差率

2. 广义维纳过程的基本概念

3. 具体使用

四、伊藤过程

五、几何布朗运动

六、伊藤引理

1. 基本概念

2. 具体使用

七、对数正态分布

一、马尔可夫过程（Markov）

1. 基本概念

Q：为什么要讲马尔可夫过程？

A：因为通常假设股票价格服从马尔可夫过程。

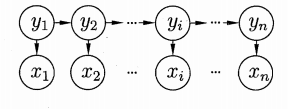
马尔可夫过程：只有标的变量的当前值与未来的预测有关，变量的历史值以及变量从过去到现在的演变方式与未来的预测无关。

弱型市场有效性：股票的当前价格包含了过去价格的所有信息。

两者是一致的，投资者不能通过历史数据来获得高于平均收益率的收益。这也就是为什么 “通常假设股票价格服从马尔可夫过程” 吧？

2. 具体使用

考虑一个服从马尔可夫过程的变量，在 T 时间内该变量的变化量服从正态分布：

$\phi (\mu, \nu )=\phi (0, T)$

μ 是均值，v 是方差。

由于变量服从马尔可夫过程，因此变量过去的变化不会影响变量未来的变化，从而变量的变化量服从的是独立同分布的正态分布。两个独立的正态分布之和仍是正态分布。

(1) 变量在 2T 时间内的变化量的概率分布是什么？

在 2T 时间内的变化量 = 在 0~T 时间内的变化量 + 在 T~2T 时间内的变化量

$\phi (0, 2T)$

(2) 变量在 0.5T 时间内的变化量的概率分布是什么？

2 * 在 0.5T 时间内的变化量 = 在 0~T 时间内的变化量

$\phi (0, 0.5T)$

(3) 变量在 Δt 时间内的变化量的概率分布是什么？

n * 在 Δt 时间内的变化量 = 在 0~T 时间内的变化量

$\phi (0, T/n)$

二、维纳过程

1. 基本概念

维纳过程：是一种均值为 0，方差为每年 1.0 的特殊马尔可夫过程。

性质1：在一小段时间区间 Δt 内的变化量 Δz 为

$\Delta z=\varepsilon \sqrt{\Delta t}$

其中 ε 服从标准正态分布。从而 Δz 也服从正态分布：

$\phi (0, \Delta t)$

性质2：在任何两个不相重叠的 Δt 时间区间内，变化量 Δz 之间相互独立。

性质 2 说明变量 z 服从马尔可夫过程，εi 之间也是相互独立的。

2. 具体使用

考虑一段时间 T 内 z 的变化。我们可以将变化量表示为 z(T)-z(0)，这一变化量可以被看成是在 N 个长度为 Δt 的小时间段内变量 z 变化的总和，其中

$N=\frac{T}{\Delta t}$

因此

$z(T)-z(0)=\sum_{i=1}^{N}\varepsilon _{i}\sqrt{\Delta t}$

由维纳过程的性质 2 我们知道 εi 之间相互独立，因此上式也服从正态分布：

$\phi (0, N\Delta t )=\phi (0, T)$

三、广义维纳过程

1. 漂移率和方差率

漂移率：变量在每单位时间内均值的变化。
方差率：变量在每单位时间内的方差。

我们刚才讨论的维纳过程又称基本维纳过程，它的漂移率为 0，方差率为 1，意味着将来任意时刻 z 的期望值都等于当前值，并且在长度为 T 的任何时间内其变化量的方差都等于 T 。

显然，上述情况过于特殊了，因此我们推广到广义维纳过程。

2. 广义维纳过程的基本概念

定义变量 x 满足下式：

$dx=adt+bdz$

其中 a 和 b 是常数。

adt 项说明变量 x 的单位时间漂移率为 a 。

假设没有 bdz 项，则上式变为 dx=adt，对 t 进行积分得出：

$x=at+x_{0}$

可见，在一段时间 T 内，变量 x 的增量为 aT，从而解释了 “adt 项说明变量 x 的单位时间漂移率为 a”。

bdz 项可看成是附加在变量 x 路径上的噪声或扰动，其幅度是基本维纳过程的 b 倍。

3. 具体使用

由于 z 服从基本维纳过程，因此我们可以把式子写成：

$dx=adt+b\varepsilon \sqrt{dt}$

在短时间 Δt 内则有

$\Delta x=a\Delta t+b\varepsilon \sqrt{\Delta t}$

ε 服从标准正态分布，因此 Δx 也服从正态分布：

$\phi (a\Delta t , b^{2}\Delta t )$

四、伊藤过程

广义维纳过程中 a 和 b 都是常数，而伊藤过程是一种更为广义的维纳过程，即 a 和 b 是变量 x 和时间 t 的函数。

伊藤过程定义变量 x 满足下式：

$dx=a(x,t)dt+b(x,t)dz$

其中，漂移率 a 和方差率 b^2 都会随时间变化。但由于它们只依赖 x 在时间 t 的值，因此该过程仍然具有马尔可夫性质。

在短时间 Δt（t 到 t+Δt）内则有

$\Delta x=a(x,t)\Delta t+b(x,t)\varepsilon \sqrt{\Delta t}$

上式是一个近似式，其中假定漂移率 a 和方差率 b^2 都是常数，即等于它们在时间 t 的值。

五、几何布朗运动

我们倒回去考虑广义维纳过程。

假设股票在 t 时刻的价格为 S，如果我们直接把它扔进广义维纳过程，则会得到：

$dS=\mu dt+\sigma dz$

这样的股票价格模型忽略了一个问题：投资者所要求的期望收益率实际上与股票价格无关：

股票收益率的期望值 = 常数
股票收益率的期望值 = 股票价格的漂移率 / 股票价格
股票价格的漂移率 / 股票价格 = 常数
股票价格的漂移率 = 股票价格 × 常数

因此，上式应该修正为：

$dS=\mu S dt+\sigma Sdz$

常数 μ 就是股票收益率的期望值，或写作

$\frac{dS}{S}=\mu dt+\sigma dz$

在短时间 Δt 内则有

$\frac{\Delta S}{S}=\mu \Delta t+\sigma \varepsilon \sqrt{\Delta t}$

变量说明：

变量 μ 为股票价格的期望收益率
变量 σ 为股票价格的波动率
变量 σ^2 为股票价格的方差率

在风险中性世界里，μ 等于无风险利率 r 。

六、伊藤引理

1. 基本概念

我们已经知道伊藤过程定义变量 x 满足下式：

$dx=a(x,t)dt+b(x,t)dz$

其中 dz 是维纳过程，a 和 b 是 x 和 t 的函数。变量 x 的漂移率为 a，方差率为 b^2 。

伊藤引理说明一个 x 和 t 的函数 G(x, t) 服从以下过程：

$dG=(\frac{\partial G}{\partial x}a +\frac{\partial G}{\partial t}+\frac{1}{2}\frac{\partial^2 G}{\partial x^2}b^{2})dt+\frac{\partial G}{\partial x}bdz$

漂移率：

$\frac{\partial G}{\partial x}a +\frac{\partial G}{\partial t}+\frac{1}{2}\frac{\partial^2 G}{\partial x^2}b^{2}$

方差率：

$(\frac{\partial G}{\partial x})^{2}b^{2}$

2. 具体使用

前面我们已经推导了：

$dS=\mu S dt+\sigma Sdz$

代入伊藤引理给出的公式，得到：

$dG=(\frac{\partial G}{\partial S}\mu S +\frac{\partial G}{\partial t}+\frac{1}{2}\frac{\partial^2 G}{\partial S^2}\sigma ^{2}S^{2})dt+\frac{\partial G}{\partial S}\sigma Sdz$

七、对数正态分布

下面来推导 lnS 所服从的随机过程，定义：

$G=lnS$

求导

$\frac{\partial G}{\partial S}=\frac{1}{S},\frac{\partial^2 G}{\partial S^2}=-\frac{1}{S^{2}},\frac{\partial G}{\partial t}=0$

代入

$dG=(\frac{\partial G}{\partial S}\mu S +\frac{\partial G}{\partial t}+\frac{1}{2}\frac{\partial^2 G}{\partial S^2}\sigma ^{2}S^{2})dt+\frac{\partial G}{\partial S}\sigma Sdz$

得到

$dG=(\mu -\frac{\sigma ^{2}}{2})dt+\sigma dz$