数字信号处理9：Z变换(1)

说实话，这两天看Z变换看的迷迷糊糊的，就觉得它求卷积的时候好用，再剩下的，我怎么感觉用处不大。

首先来说z变换： $X(n)\equiv \sum_{n=-\infty}^{n=\infty}x(n)z^{-n}$ ,或者简单一点的可以这样子写： $X(z)\equiv Z\left\{x(n)\right\}$ ，感觉Z变换最重要的一个问题是收敛性，因为Z变换时无限幂级数，而我们要保证它存在，就要使z的值让级数收敛，所以，在使用Z变换的时候，要指明他的收敛域。

对于一个给定的变换， $z^{-n}$ 的系数时信号在时间n的值：

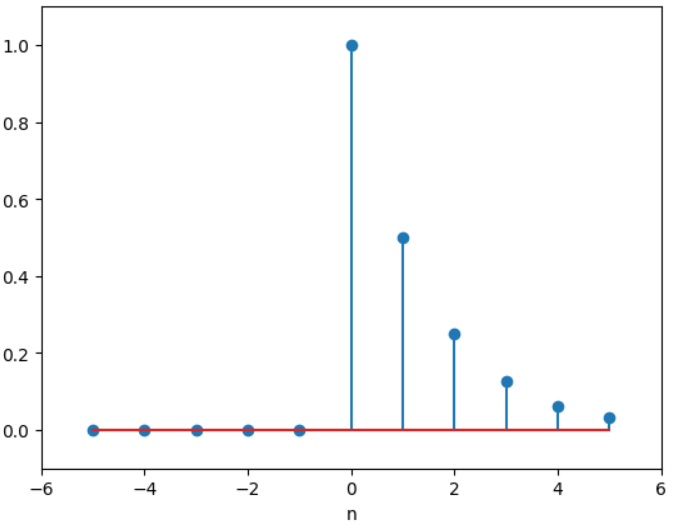
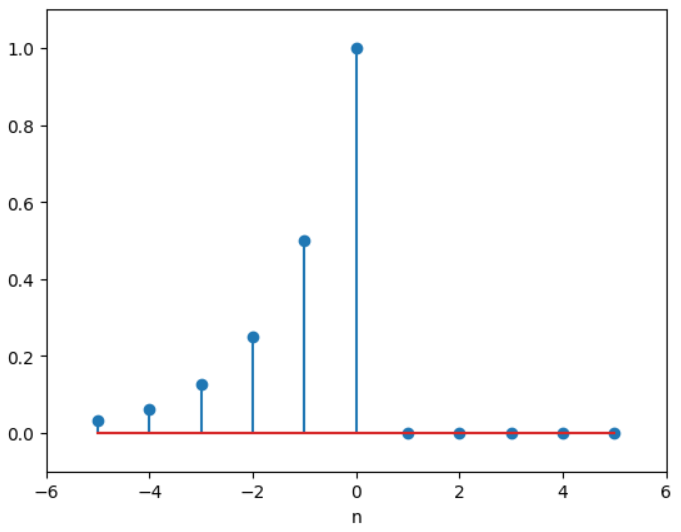
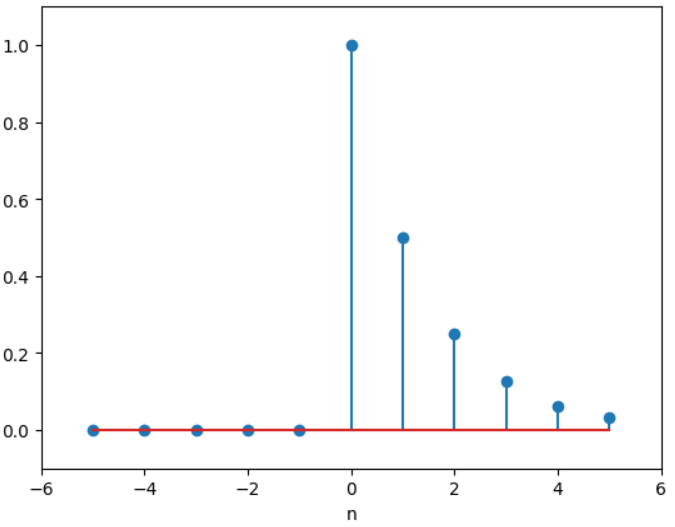
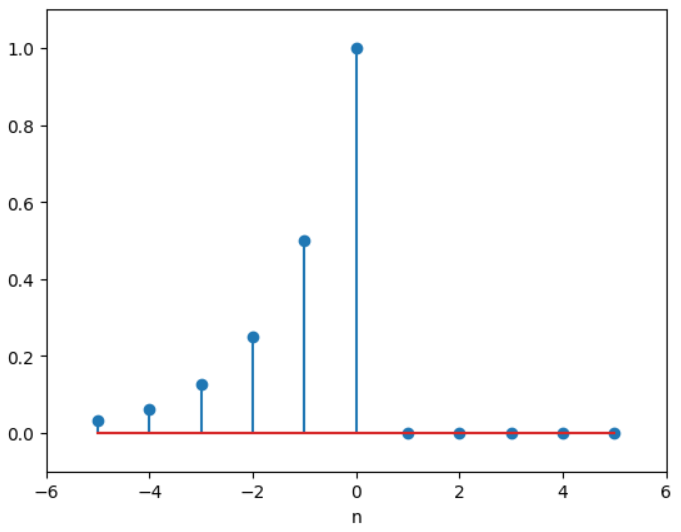
假设我们现在有一个信号： $x(n)=\left\{1,3,5,7,9,\cdots,\right\}$ ，我们就通过Z变换的方法来对这个信号进行转换： $x(z)=1+3z^{-1}+5z^{-2}+7z^{-3}+9z^{-4}+\cdots$ ，同时，我们要指明，这个信号序列，他的收敛域时除了 $z=0$ 以外的整个z平面。

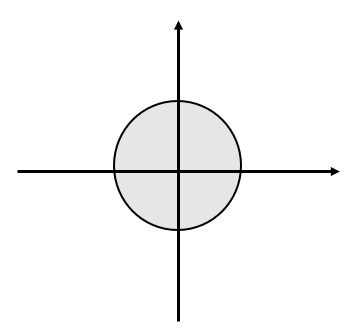
z平面是个复平面，横轴是实部，纵轴是虚部，在通过对X(z)进行分析，以判断其极点、零点，然后就得到了一个z变换的收敛域，注意，z变换的收敛域非常重要，因为，z变换的闭合形式的表达式时不能唯一的表示时域信号的，它所表的的是个很模糊的概念，我们如果要解决这个模糊性，唯一的方法就是在闭合形式的表达式给出后，通过给定收敛域的方式来确定一个信号。简单的理解就是一个离散时间信号时由他的z变换和z变换的收敛域共同决定的。

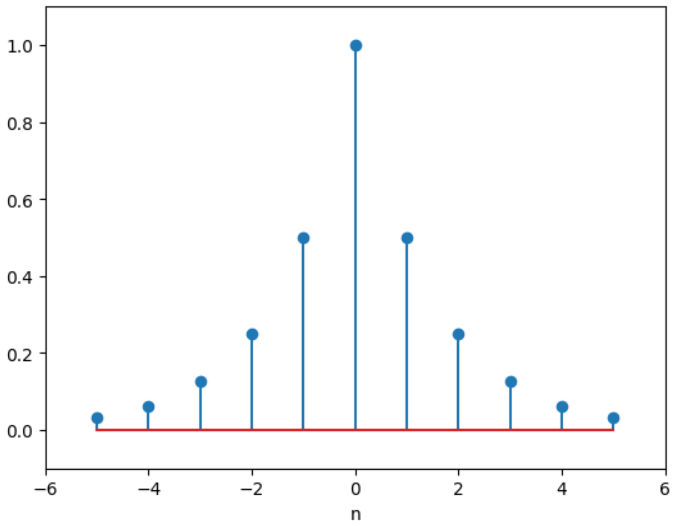
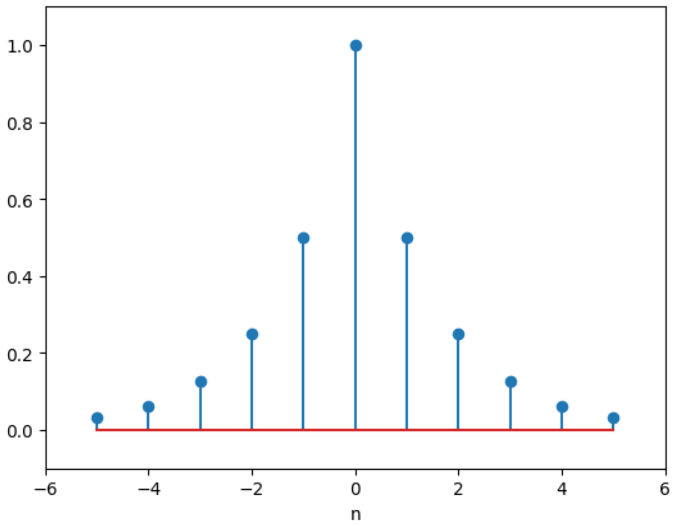
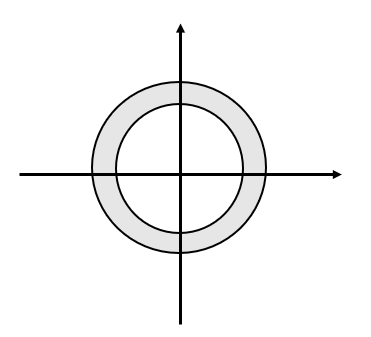
如果一个无限长双边信号好都有收敛域，那么这个收敛域就是z平面上的环状区域，而信号的收敛域是取决于信号的长的及该信号是否为因果、非因果或者双边信号，而如果说，x(n)是因果信号，那么单边和双边z变换时一样的，但是在其他情况下，可能是不同的。

跟着书上的图，我们来看一下各种信号的收敛域：

信号		收敛域
有限长信号
因果		除z=0外整个z平面
非因果		除z=∞外整个z平面
双边		除z=0和z=∞外整个z平面
无限长信号
因果		\|z\|>r
非因果		\|z\|<r
双边		r2<z<r1

就是说，当你在做z变换的时候，要注意变换的收敛域。

Z变换的性质：

1、线性：

信号的线性组合的z变换和z变换的线性组合时相同的，也就是说，如果一个信号可以认为时多个信号的叠加，我们对这个信号的Z变换和我们对每个信号Z变换之后进行叠加的效果时相同的，但是还是要注意，对每个信号的收敛域要取交集，

2、时移：

公式：

$if: x(n)\overset{z}{\leftarrow}\overset{}{\rightarrow}X(z)$

$then: x(n-k)\leftrightharpoons z^{-k}X(z)$

这是我觉得除了卷积以外最有用的性质了。

如果说，若干个信号的线性组合有有限时长，那么其z变换的收敛域是由信号的有限长不知决定的，而不是由各个变换的收敛域决定。

3、尺度变换：

$\begin{matrix} if :x(n)\leftrightharpoons X(z),r_1<|z|<r_2\\\ then:a^nx(n)\leftrightharpoons X(a^{-1}z),|a|r_1<|z|<|a|r_2 \end{matrix}$

这个很容易理解，你都把时域信号的尺度给变了，z域当然也要跟着变的，没什么好说的。

4、时间反转：

$\begin{matrix} if :x(n)\leftrightharpoons X(z),r_1<|z|<r_2\\\ then:x(-n)\leftrightharpoons X(z^{-1}),\frac{1}{r_2}<|z|<\frac{1}{r_1} \end{matrix}$

5、z域求导：

$\begin{matrix} if :x(n)\leftrightharpoons X(z)\\\ then:nx(n)\leftrightharpoons -z\frac{dX(z)}{dz} \end{matrix}$

6、两序列卷积：

这是我觉得最有用的，两个在时域的卷积很麻烦，但是到z域直接将两个z变换相乘即可：

$\begin{matrix} if :x_1(n)\leftrightharpoons X_1(z)\\\ and :x_2(n)\leftrightharpoons X_2(z)\\\ then:x(n)=x_1(n)*x_2(n)\leftrightharpoons X(z)=X_1(z)X_2(z)\end{matrix}$

7、两序列相关：

$\begin{matrix} if :x_1(n)\leftrightharpoons X_1(z)\\\ and :x_2(n)\leftrightharpoons X_2(z)\\\ then:r_{x_1x_2}(l)=\sum_{n=-\infty}^{\infty}x_1(n)x_2(n-l)\leftrightharpoons R_{x_1x_2}(z)=X_1(z)X_2(z^{-1})\end{matrix}$

其实从这里，你也能大致的知道自相关怎么计算。

8、两序列相乘：

$\begin{matrix} if :x_1(n)\leftrightharpoons X_1(z)\\\ and :x_2(n)\leftrightharpoons X_2(z)\\\ then:x(n)=x_1(n)x_2(n)\leftrightharpoons X(z)=\frac{1}{2\pi j} \oint_{C}X_1(v)X_2(\frac{z}{v})v^{-1}dv \end{matrix}$

说实话，我只想懂原理，不想算。

9、帕斯瓦关系式（我实在没搞懂这个有啥用，所以就写个公式）：

$\sum_{n=-\infty}^{\infty}x_1(n)x_2^*(n)=\frac{1}{2\pi j} \oint_{C}X_1(v)X_2^*(\frac{1}{v^*})v^{-1}dv$

10、初值定理：

如果x(n)是因果的，那么：

$x(0)=\lim_{z\rightarrow \infty}X(z)$

这个到后面再解释，因为后面到有理Z变换会详细的讲极点和零点在Z变换中的相关问题。

这里给出有些常见的Z变换对：

信号		Z变换	收敛域
1	$\delta(n)$	$1$	$\forall z$
2	$u(n)$	$\frac{1}{1-z^{-1}}$	$\|z\|>1$
3	$a^nu(n)$	$\frac{1}{1-az^{-1}}$	$\|z\|>\|a\|$
4	$na^nu(n)$	$\frac{az^{-1}}{(1-az^{-1})^2}$	$\|z\|>\|a\|$
5	$-a^nu(-n-1)$	$\frac{1}{1-az^{-1}}$	$\|z\|<\|a\|$
6	$-na^nu(-n-1)$	$\frac{az^{-1}}{(1-az^{-1})^2}$	$\|z\|<\|a\|$
7	$cos(\omega_0 n)u(n)$	$\frac{1-z^{-1}cos\omega_0}{1-2z^{-1}cos\omega_0+z^{-2}}$	$\|z\|>1$
8	$(sin\omega_0 n)u(n)$	$\frac{z^{-1}sin\omega_0}{1-2z^{-1}cos\omega_0+z^{-2}}$	$\|z\|>1$
9	$a^ncos(\omega_0 n)u(n)$	$\frac{1-az^{-1}cos\omega_0}{1-2az^{-1}cos\omega_0+a^2z^{-2}}$	$\|z\|>\|a\|$
10	$a^n(sin\omega_0 n)u(n)$	$\frac{az^{-1}sin\omega_0}{1-2az^{-1}cos\omega_0+a^2z^{-2}}$	$\|z\|>\|a\|$

这个表是最有用的了

有理Z变换：

这里呢，主要就说的是个零点和极点，非常好理解，零点就是使 $X(z)$ 为0的点，极点就是使 $X(z)$ 趋于无穷的点，如果我们用 $X(z)=\frac{B(z)}{A(z)}$ 来表示 $X(z)$ ，那么使得B(z)=0的点就是零点，使得A(x)=0的点就是极点。

这里介绍一个很重要的图：零极点图：把 $X(z)$ 在复平面上画出来，用x记号来表示极点位置，用O来表示零点位置，多阶零、极点的阶数就在记号旁边用数字表示，一个Z变换的收敛域不能包含任何极点。

Z变换 $X(z)$ 是复变量 $z=real(z)+imag(z)j$ 的复函数，很显然， $X(z)$ 的幅值 $|X(z)|$ 是z的实正函数。

因果信号的几点位置和时域行为：

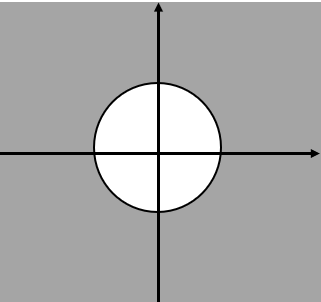
这里我们先介绍一个基本的概念：单位圆：|z|=1

如果，

s1、一个信号的Z变换的极点在单位圆内，那这个信号就是衰减的；

s2、一个信号的Z变换的极点在单位圆上，那这个信号是恒定的；

s3、一个信号的Z变换的极点在单位圆外，那这个信号是增长的；

负极点会导致信号的符号交替，而且我们要避免单位圆外的因果信号，因为根据s3，这个信号是增长的，最终会达到无界，导致计算机系统出现上溢。

同时，位于单位圆上的实的双重极点的结果是无界的信号，

具有实极点或者是复共轭极点，并且这些极点都位于单位圆内或者单位圆上的实因果信号的幅度总是有界的；具有一个和原点越近的极点（一对复共轭极点）的信号，比具有一个位于单位圆内且接近单位元的极点的信号衰减更快。

由上可知：信号的时域行为主要取决于其极点相对应单位圆的位置，零点也会影响信号的行为，但是没有极点的影响大。

Z逆变换：主要有三种常用方法：

1、直接求围线积分：

$x(n)=\frac{1}{2\pi j}\oint_{C}X(z)z^{n-1}dz$

2、展开成变量 $z$ 和 $z^{-1}$ 的级数

3、部分分式展开并查表（这个就用的线性性质，而且书里例题大多都用这种方法，比较简单些）：

这里要注意两个概念：

1、相异极点：

设极点 $p_1,p_2,\cdots,p_n$ 全部不同，要求的是下式中的A：

$\frac{X(z)}{z}=\frac{A_1}{z-p_1}+\frac{A_2}{z-p_2}+\cdots+\frac{A_n}{z-p_n}$

2、多重极点：

如果 $X(z)$ 有一个l重极点，也就是说，分母中包含有因式： $(z-p_k)^l$ ,那就不是上面的式子可以解决的了，这个我还没学完，还没完全了解，就先写到这。

说实话，我觉得知道逆变换和会实现逆变换就行了，因为常用的这三种方法都太麻烦了，一般来说根本用不着，除了大学生考试，谁还给你弄这让你手算，都是已经实现好的封装，直接调用就行。

比如说，我找了找，用Scipy中的signal库就可以实现：

# 首先使用zpk2tf以零点-极点形式的系统函数转换为传输函数，
# 其中[]表示该系统没有零点或极点，x为传入的离散信号x(n)。
# 使用tf2zpk将传输函数转换为零点-极点形式，该函数返回的结果就是离散信号x(n)的z变换结果；
def z_transform(x):
    b, a = signal.zpk2tf([], [], x)
    return signal.tf2zpk(b, a)