写在前面

这里主要了解一下分位数归一化（Quantile Normalization, QN）。如无特殊说明时，本文中的QN作为分位数归一化的缩写。

Quantile Normalization 直接翻译是 分位数归一化，但也有翻译为分位数标准化。笔者理解是按直译叫分位数归一化，但是按数据的处理方式，应该叫分位数标准化，按英文的话就一种：Quantile Normalization。之所以有标准化和归一化两种说法，是因为它们是两种不同的处理方式。

本文暂统一名称叫分位数归一化(QN)。

标准化/归一化

标准化（standardization）、归一化（normalization）两者总是被混着叫，实际是在做什么处理呢？

先看下Python库中的关于预处理的一些包：

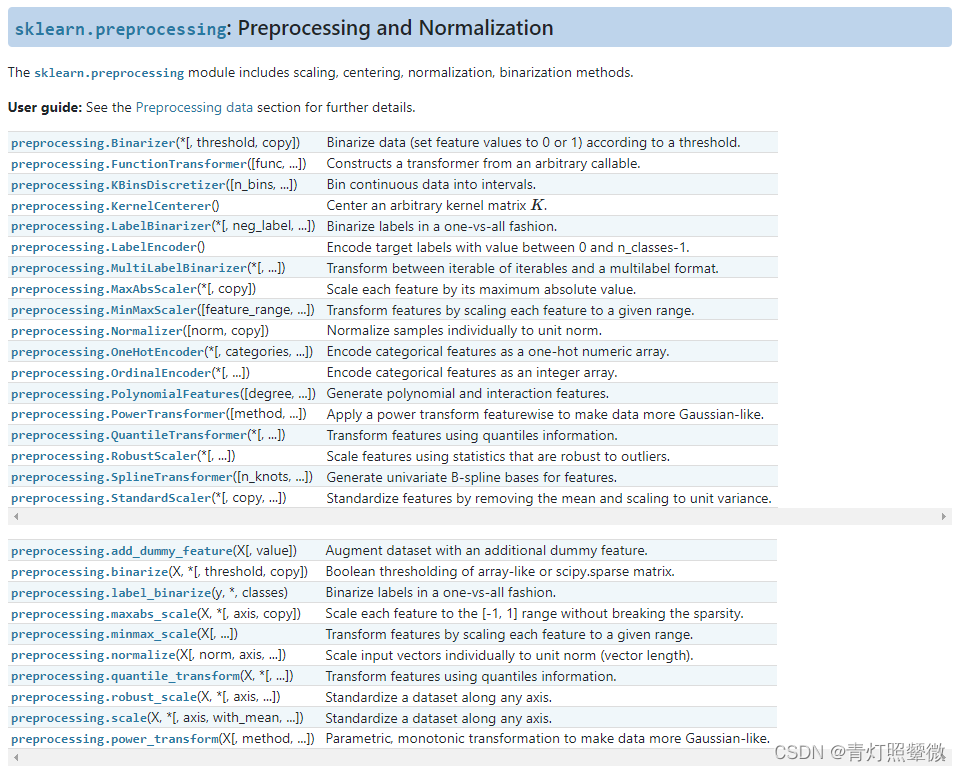
其中包括了：scaling(缩放), centering(中心化), normalization(归一化), binarization(二值化)。

对于标准化和归一化对应的常用的模块：

• 标准化 standardization：py模块 StandardScaler 是常用的标准化数据处理，对应z-score标准化公式：$z=\frac{x-\mu }{s}$（其中，$\mu$是训练样本的均值，$s$是训练样本的标准差）。将原始数据转换为均值为0，方差为1的新数据，也是把数据缩放(scaling)到特定区间上。该处理从公式计算上解读为：当前数据比总体均值多了几个标准差；从数据整体上解读为：把原数据标准化缩放为服从标准正态分布的数据。

• 归一化 normalization：py模块 MinMaxScaler是比较常用的归一化方法：min-max归一化，$x^{\ast }=\frac{x_i-x_{min}}{x_{max}-x_{min}}$。

python模块qnorm实现分位数归一化

仔细看Python的sklearn库中（# 标准化/归一化 部分的截图），会发现这里没有分位数归一化的包。是的，sklearn里没有QN。需要先安装qnorm（qnorm安装包官网），安装命令为：pip install qnorm。使用示例如下：

import pandas as pd
import qnorm

df = pd.DataFrame({'C1': {'A': 5, 'B': 2, 'C': 3, 'D': 4},
                   'C2': {'A': 4, 'B': 1, 'C': 4, 'D': 2},
                   'C3': {'A': 3, 'B': 4, 'C': 6, 'D': 8}})

print(qnorm.quantile_normalize(df, axis=1))

执行后可得到：

R代码实现分位数归一化

最初测试使用了R代码，在“INSCODE AI创作助手”助手的默认实现方式中也使用了R。（做分位数归一化处理可能用R的比较多）

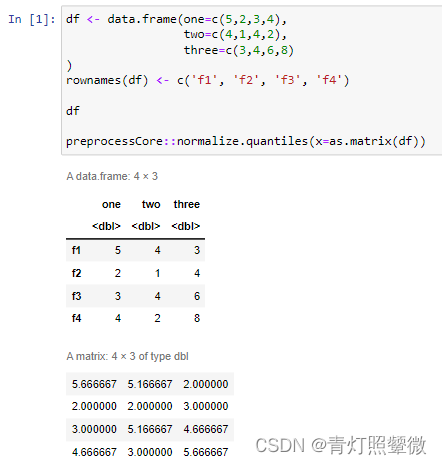
代码中使用到R包preprocessCore：

df <- data.frame(one=c(5,2,3,4),
                 two=c(4,1,4,2),
                 three=c(3,4,6,8)
)
rownames(df) <- c('f1', 'f2', 'f3', 'f4')

df

preprocessCore::normalize.quantiles(x=as.matrix(df))

执行后得到：

分位数归一化 - NSCODE AI创作助手的回答

上面的代码直接执行就能得到相应的数据，下面是通过“NSCODE AI创作助手”了解更多分位数归一化相关的知识。

想了解一个概念最好的方式，就是通过提问并回答这个3W1H：Waht/Why/When/How … the “A”？

1. 什么是分位数归一化（What）
2. 为什么要做分位数归一化（Why）
3. 什么时候做分位数归一化（When）
4. 怎么做分位数归一化（How）

试试“INSCODE AI创作助手”给出的一些解答：

提问示例：

来自 InsCode AI创作助手 的回答：(结果还是挺出乎意料的）

Q1：Quantile Normalization是什么？

Quantile normalization是一种用于处理高通量基因表达数据的方法。它通过对所有样本的数据进行排序，并将排序后的数据进行归一化，从而消除任何来自各个样本之间的数据不一致性的影响。基本思路是将每个样本的数据值按照从小到大的顺序进行排列，然后将排列后的数据值替换为对应分位数（例如，对于一个样本，将第10个最小值替换为第10个最小分位数）。这个过程使得每个样本的数据分布相同，从而可以进行更好的比较和综合分析。

Q2-1: 什么时候用Quantile normalization？

Quantile normalization是一种数据预处理方法，通常在基因表达数据中使用。当数据集中存在分布不均的情况时，使用Quantile normalization可以将数据集中的样本在数值分布上进行对齐，以消除由于样本差异而带来的数据偏差。因此，当你想要在基因表达数据分析中对不同样本的基因表达数据进行比较时，可能需要使用Quantile normalization来消除样本之间的差异，以确保数据的准确性和可靠性。

Q2-2: 什么时候做Quantile normalization？

Quantile normalization通常在对基因表达数据进行比较分析时使用。具体地说，当你有多个实验组（每组都包含多个样本）且你想比较它们之间的基因表达水平时，通常会使用Quantile normalization进行数据标准化，以消除混杂因素（例如实验批次，RNA提取和扫描阅读器）对实验结果的影响。这样可以使得样本之间的差异仅仅是由于生物学的差异，而不是技术方面的差异所引起的。因此，Quantile normalization 常被用于微阵列和RNA测序数据分析，以减少技术方面的差异对于样本之间的比较所带来的影响。

Q3：为什么要做Quantile Normalization？

Quantile normalization是一种数据标准化方法，它的目的是通过调整数据的排名顺序来消除实验中不同样本之间的技术差异，使得数据能够更好地比较和分析。
在高通量基因表达研究中，由于实验过程、实验条件等因素的不同，不同样本之间的基因表达量数据往往存在一定的不一致性。如果直接进行差异分析或聚类分析等，可能会将这些技术差异误认为是生物差异，导致分析结果出现偏差。因此，需要对数据进行标准化处理，消除这些技术差异。
Quantile normalization的做法是将不同样本中基因表达量的排名顺序进行统一，使得各个样本的数据分布在相同的位置上。这样可以消除技术差异，让不同样本之间成为可比较的数据，提高了分析结果的可信度和稳定性。

Q3问题重新生成：（得到类似但不同的结果）
Quantile normalization是一种常用的数据标准化方法，主要应用于高通量基因表达数据分析中。做Quantile normalization的目的是消除样本之间的技术变异（如批次效应、不同实验处理等）与生物变异对基因表达量的影响，使得样本间的基因表达值具有可比性。
Quantile normalization的具体步骤是将每个样本的基因表达值按照从小到大的顺序排列，然后将排名相同的基因表达值分配给相应的样本，从而使得每个基因在不同样本中的表达值的分布均匀，且每个样本的基因表达量分布保持不变。
通过Quantile normalization，我们可以快速、有效地比较不同样本之间的基因表达量差异，从而有助于进一步发现基因调控机制、诊断疾病等方面的研究。

Q4-1: 如何做Quantile normalization？

Quantile normalization是一种数据标准化方法，用于将不同样本之间的数据分布进行比较和统一。以下是基于R语言的实现方法：

1. 导入需要进行标准化处理的数据集。
2. 对数据集进行排序。

data_sorted <- apply(data, 2, sort)

3. 计算每一行的分位数。

quantiles <- apply(data_sorted, 1, quantile, probs = seq(0, 1, length = nrow(data) + 1))

4. 对数据集进行标准化。

data_norm <- apply(data, 2, function(x) {
  rank <- order(x)
  quantiles[rank]
})

5. 对标准化后的数据进行检查。

summary(apply(data_norm, 2, quantile, probs = seq(0, 1, length = nrow(data) + 1)))

以上就是Quantile Normalization的基本实现方法。

对Q4问题竟然直接给出代码的示例还是有些惊喜的，代码是直接实现的，我以为会直接调用归一化处理的R包:preprocessCore，至于代码准确性还有待测试。我还是希望用Python给出答案，就发出提问：

Q4-2: 如何用python做Quantile Normalization？

Quantile normalization是一种常见的数据预处理技术，用于将不同样本或实验的数据进行标准化，使得它们具有相同的分布。下面是一个用Python实现Quantile Normalization的示例代码：

import numpy as np
from scipy.stats import rankdata

def quantile_normalize(data):
    # 对每一列数据进行排序
    sorted_data = np.sort(data, axis=0)

    # 计算每一行的分位数
    row_quantiles = np.mean(sorted_data, axis=1)

    # 对每一列数据进行排序，并将其映射到对应的分位数
    rank_data = rankdata(data, axis=0)
    mapped_data = np.zeros_like(data)
    for i in range(data.shape[1]):
        mapped_data[:, i] = row_quantiles[rank_data[:, i]-1]

    return mapped_data

使用示例：

# 生成随机数据
data = np.random.rand(10, 5)

# 将数据进行Quantile Normalization
normalized_data = quantile_normalize(data)

该函数输入一个矩阵数据，输出一个Quantile Normalization后的矩阵。函数首先对矩阵的每一列进行排序，然后计算每一行的分位数。接着，对于每一列的数据，映射到对应的分位数。最后，输出Quantile Normalization后的矩阵。

python代码比较意外的是还添加了中文注释，不禁有些感叹自己也不一定能短时间写出这些代码。与R脚本相同，并没有使用包，而是根据QN的原理直接实现，至于代码准确性还是需要细节上的修改：

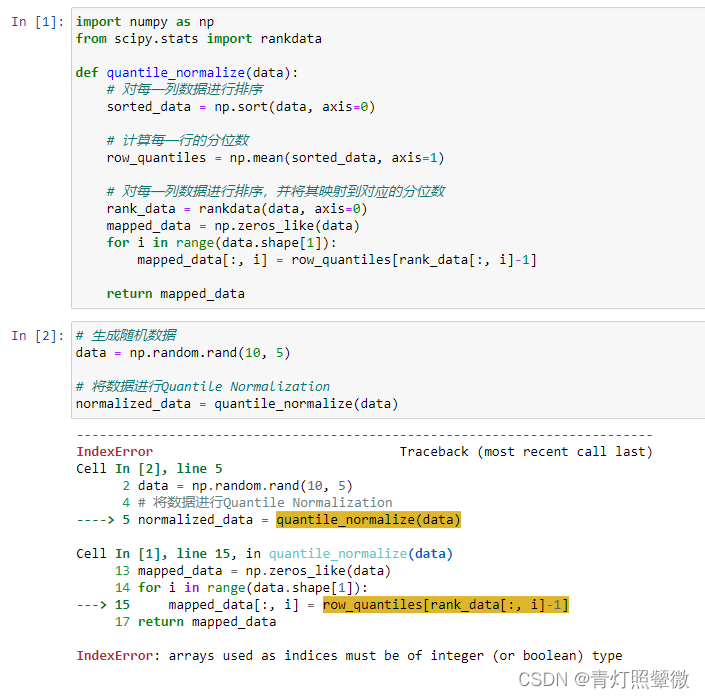
报错应该是在映射对应的分位数时错误，报错原因是根据索引获取元素时，索引应该是整数，这里rankdata输出的值是浮点型。

根据报错调整代码：

import numpy as np
from scipy.stats import rankdata

def quantile_normalize(data):
    # 对每一列数据进行排序
    sorted_data = np.sort(data, axis=0)

    # 计算每一行的分位数
    row_quantiles = np.mean(sorted_data, axis=1)
    
    # 对每一列数据进行排序，并将其映射到对应的分位数
    rank_data = rankdata(data, axis=0)
    mapped_data = np.zeros_like(data, dtype=float)  #【修改】初始化指定数据类型为浮点型
    for i in range(data.shape[1]):
        # mapped_data[:, i] = row_quantiles[rank_data[:, i]-1]
        mapped_data[:, i] = row_quantiles[[int(i) for i in rank_data[:, i]-1]]  # 【修改】索引为整型
        
    return mapped_data

注意：代码中，当一列（某样本）出现相同值（基因表达值相同）时的排位问题，直接按计算排位均值后下取整数来获取对应值。具体来说：某列有n个相同数值，应排位为并列第m个，此时rankdata对这n个数的排位都是：$\frac{m+(m+1)+...+(m+n-1)}{n}$，比如，有2个数都排位第3个，则在rankdata排位为：$\frac{3+4}{2}=3.5$，代码中取整(int是下取整)，则为3；若有3个数都排位第3个，则在rankdata排位为：$\frac{3+4+5}{2}=3$，代码中取整，则为排位取3。

但是， 实际排位中，对于相同的值，使用的是排位后对应值的均值（而不是排位的均值）。也就是上面代码还需要进一步完善：对相同值的排位问题。

上面调整后的代码执行结果：

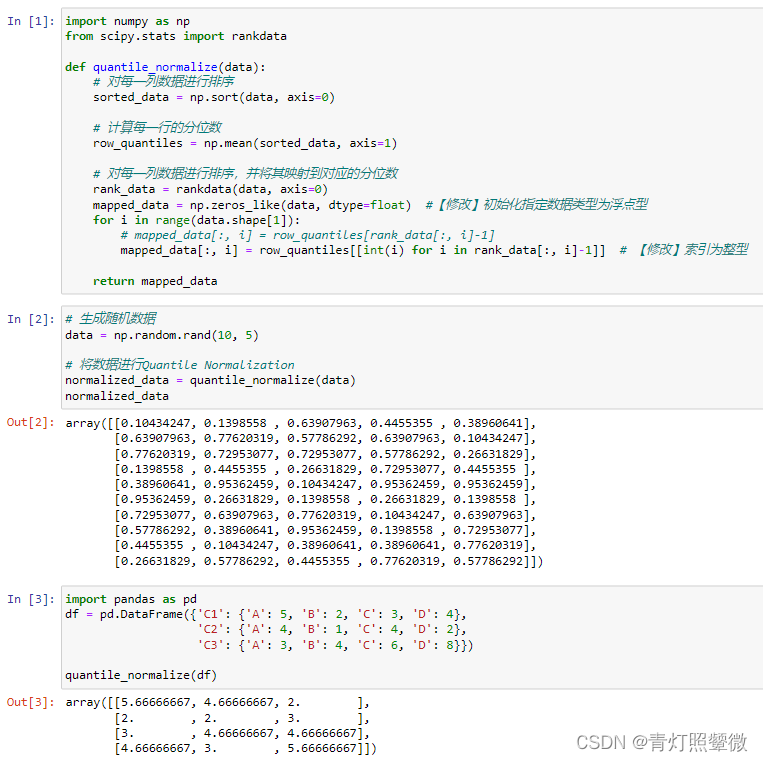
可视化分位数归一化处理前后发生的变化

先直观得看几个示例QN前后的结果，输入数据：

import pandas as pd
import qnorm
df1 = pd.DataFrame({'C1': {'A': 5, 'B': 2, 'C': 3, 'D': 4},
                   'C2': {'A': 6, 'B': 1, 'C': 7, 'D': 9},
                   'C3': {'A': 3, 'B': 4, 'C': 6, 'D': 8}})
dfn1 = qnorm.quantile_normalize(df1, axis=1)

df2 = pd.DataFrame({'C1': {'A': 5, 'B': 2, 'C': 3, 'D': 4},
                   'C2': {'A': 4, 'B': 1, 'C': 4, 'D': 2},
                   'C3': {'A': 3, 'B': 4, 'C': 6, 'D': 8}})
dfn2 = qnorm.quantile_normalize(df2, axis=1)

df3 = pd.DataFrame({'C1': {'A': 5, 'B': 2, 'C': 3, 'D': 4},
                   'C2': {'A': 4, 'B': 1, 'C': 4, 'D': 4},
                   'C3': {'A': 3, 'B': 4, 'C': 6, 'D': 8}})

dfn3 = qnorm.quantile_normalize(df3, axis=1)

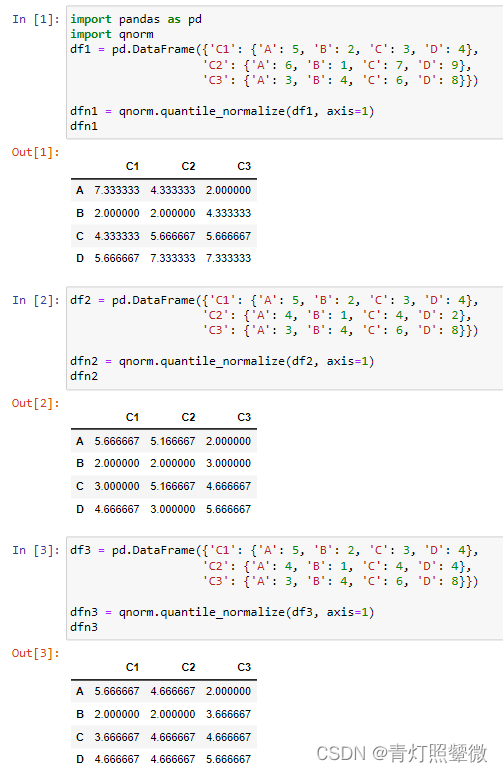
可视化QN前后的数据：

import matplotlib.pyplot as plt

fig, axs = plt.subplots(3, 2)
plt.rcParams.update({'font.size':5})
i = 0
for df, dfn in zip([df1, df2, df3], [dfn1, dfn2, dfn3]):
    axs[i, 0].scatter(range(len(df.T['A'])), df.T['A'], label='A')
    axs[i, 0].scatter(range(len(df.T['B'])), df.T['B'], label='B')
    axs[i, 0].scatter(range(len(df.T['C'])), df.T['C'], label='C')
    axs[i, 0].scatter(range(len(df.T['D'])), df.T['D'], label='D')
    axs[i, 0].legend(loc='upper left', shadow=True)
    axs[i, 0].set_xticks([0, 1, 2], [1, 2, 3])

    axs[i, 1].scatter(range(len(dfn.T['A'])), dfn.T['A'])
    axs[i, 1].scatter(range(len(dfn.T['B'])), dfn.T['B'])
    axs[i, 1].scatter(range(len(dfn.T['C'])), dfn.T['C'])
    axs[i, 1].scatter(range(len(dfn.T['D'])), dfn.T['D'])
    axs[i, 1].set_xticks([0, 1, 2], [1, 2, 3])
    i += 1
    
fig.tight_layout()
plt.show()

图分两列，左侧一列为原始数据，右侧一列分位数归一化(QN)后的数据。从原始数据到QN后的数据，可以发现，右侧图中每个样本（一列）的4个数据的排列顺序没有发生变化。（注意：有的看起来是<4个数据，是因为原始数据有相同的值，点重叠了）

手动推算一遍会更理解分位数归一化的基本思路：将每个样本的数据值按照从小到大的顺序进行排列，然后将排列后的数据值替换为对应分位数。

分位数归一化方法：http://bmbolstad.com/stuff/qnorm.pdf

step1: 每个样本的feature按从小到大排序；
step2: 与原始数据对应，获取排位后的序号（rank i/ii/iii/iv)；
step3: 计算从小到大排序之后每个featrue的算术平均数；
step4: 将step2中数据排位替换为step3中排位对应的算术平均数；

什么时候该用/不该用分位数归一化

参考：http://www.bio-info-trainee.com/2043.html

虽然前面对“INSCODE AI创作助手”的提问也有类似什么时候用QN，但是概况性回答了一些QN应用场景，没有很具体或专业的表述。

有一篇文献中专门研究了什么时候使用分位数归一化：文献pdf

该文献中给出了QN的使用策略：

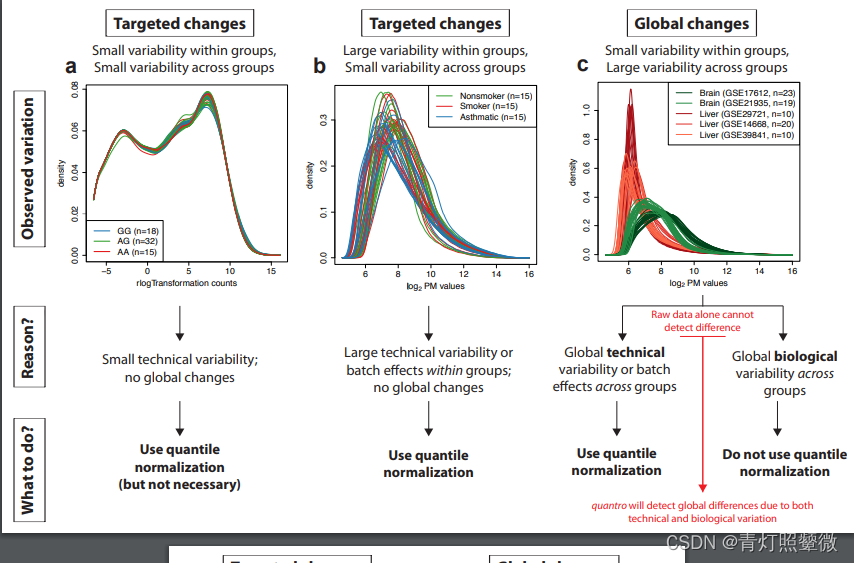
【翻译】：（没有仔细研读文献，翻译谨慎参考）

1. 组内方差小、组间方差小（变异小）→ 技术变化小，无全局变化 → 可使用QN（但是没有必要）
2. 组内方差大、组间方差小（变异小）→ 技术变化大或组内批次效应，无全局变化 → 使用QN
3. 组内方差小、组间方差大（变异大）→ 【只用原始数据不能检测到差异】→ 将 检测技术 和 生物变异 导致的全局差异
   1）组间全局技术差异或批次效应 → 使用QN
   2）组间全局生物学差异 → 不使用QN

文献中开发了quantro包：

R包quantro是：提出了一个数据驱动的方法来测试全局标准化方法的假设。证明了文献方法(quantro)的效用，通过将其应用到多个基因的表达和DNA甲基化，并显示全局标准化方法时的例子是不合适的。

---

【2023.5.31】