正则化是一组技术，可以防止神经网络中的过度拟合，从而在面对来自问题域的全新数据时提高深度学习模型的准确性。
在本文中，我们将介绍最流行的正则化技术，称为 L1、L2 和 dropout。

1. 回顾：过拟合

训练神经网络时最重要的方面之一是避免过度拟合。

然而，让我们快速回顾一下：过度拟合是指神经网络对训练数据进行很好的建模但在看到来自同一问题域的新数据时失败的现象。过度拟合是由神经网络在训练过程中拾取的训练数据中的噪声引起的，并将其作为数据的基本概念进行学习。

然而，这种习得的噪声对于每个训练集都是独一无二的。一旦模型看到来自同一问题域的新数据，但不包含这种噪声，神经网络的性能就会变得更差。

“为什么神经网络首先会接收到这种噪音？”

这样做的原因是这个网络的复杂度太高了。右侧图像显示了具有更高复杂性的神经网络的拟合。

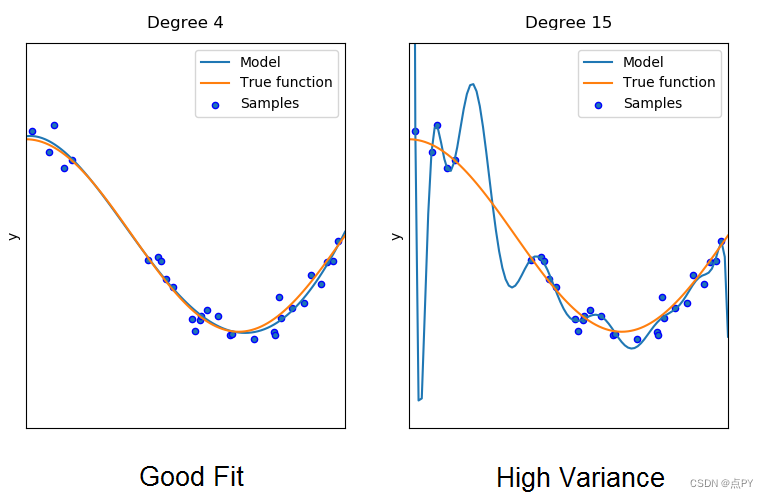
图 1. 具有良好拟合和高方差的模型。资料来源：https 😕/www.researchgate.net/publication/332412613

具有更高复杂性的模型能够拾取和学习数据中仅由某些随机波动或错误引起的模式（噪声）。网络将能够对分布的每个数据样本进行一个一个的建模，而不会识别描述分布的真实函数。

使用真实函数生成的新任意样本与模型的拟合距离很远。我们还说该模型具有高方差。

另一方面，左侧的复杂度较低的网络通过不太努力地对每个数据模式单独建模来更好地建模分布。

在实践中，过度拟合会导致神经网络模型在训练期间表现非常好，但在面对全新数据的推理期间，表现会变得更差。

简而言之：不太复杂的神经网络不太容易过度拟合。为了防止过度拟合或高方差，我们必须使用称为正则化的东西。

2.什么是正则化？

简单来说：正则化是指一组不同的技术，可以降低神经网络模型在训练过程中的复杂度，从而防止过度拟合。

我们将在下面讨论三种非常流行且有效的正则化技术，称为L1、L2和 dropout。

3. L2正则化

L2 正则化是所有正则化技术中最常见的类型，通常也称为权重衰减或 Ride 回归。

这种正则化的数学推导，以及为什么这种方法可以减少过度拟合的数学解释，是相当长和复杂的。由于这是一篇非常实用的文章，我不想过多地关注数学。相反，我想传达这项技术背后的直觉，最重要的是如何实施它，以便您可以在深度学习项目中解决过度拟合问题。

在 L2 正则化期间，神经网络的损失函数由所谓的正则化项扩展，这里称为Ω。

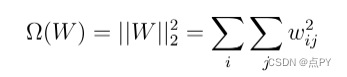
正则化项Ω定义为权重矩阵的欧几里德范数（或 L2 范数），它是权重矩阵所有平方权重值的总和。正则化项由标量 alpha 除以二来加权，并添加到为当前任务选择的正则损失函数中。这导致损失函数的新表达式：

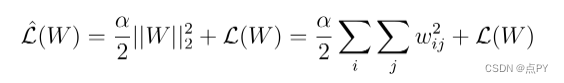
Alpha 有时称为正则化率，是我们引入神经网络的额外超参数。简单地说，alpha 决定了我们对模型进行正则化的程度。

在下一步中，我们可以计算新损失函数的梯度并将梯度放入权重的更新规则中：

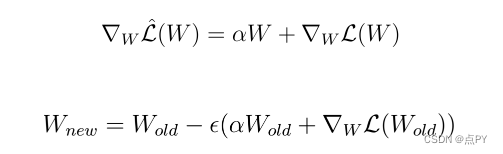
更新规则的一些重新表述导致表达式非常像常规梯度下降期间权重的更新规则：

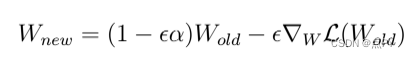
唯一的区别是，通过添加正则化项，我们从当前权重（等式中的第一项）中引入了额外的减法。

换句话说，与损失函数的梯度无关，每次执行更新时，我们都会使权重变小一点。

4. L1正则化

在 L1 正则化（也称为套索回归）的情况下，我们只需使用另一个正则化项Ω。此项是权重矩阵中权重参数的绝对值之和：

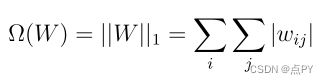
与前面的情况一样，我们将正则化项乘以 alpha，并将整个结果添加到损失函数中。

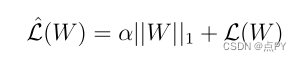
新损失函数的导数导致以下表达式，它是旧损失函数的梯度和权重值的符号乘以 alpha 的总和。

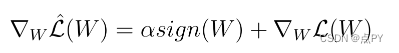
5. 为什么 L1 和 L2 正则化有效？

您现在可能会问自己的问题是：

“为什么所有这些都有助于减少过度拟合问题？”

让我们来解决这个问题。

请考虑 和 函数的绘图，其中表示在 L1 期间执行的操作和在 L2 正则化期间执行的操作。

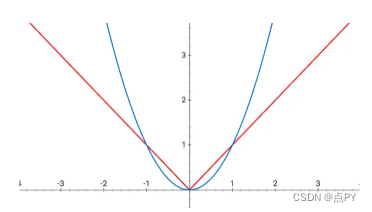
L1 功能（红色），L2 功能（蓝色）

在 L2 正则化的情况下，我们的权重参数减小，但不一定变为零，因为曲线在零附近变得平坦。另一方面，在 L1 正则化过程中，权重总是被迫一直趋向于零。

我们也可以对此采取不同的、更数学化的观点。

对于 L2，您可以考虑求解一个方程，其中权重值的平方和等于或小于值s。s是正则化项α的每个可能值都存在的常数。对于两个权重值W1和W2，该等式如下所示：w1^2 + w2^2 ≤ s

另一方面，L1 正则化可以被认为是权重值的模之和小于或等于值s的方程。这看起来像以下表达式：|W1| + |W2| ≤ s

基本上，引入的 L1 和 L2 正则化方程是约束函数，我们可以将其可视化：

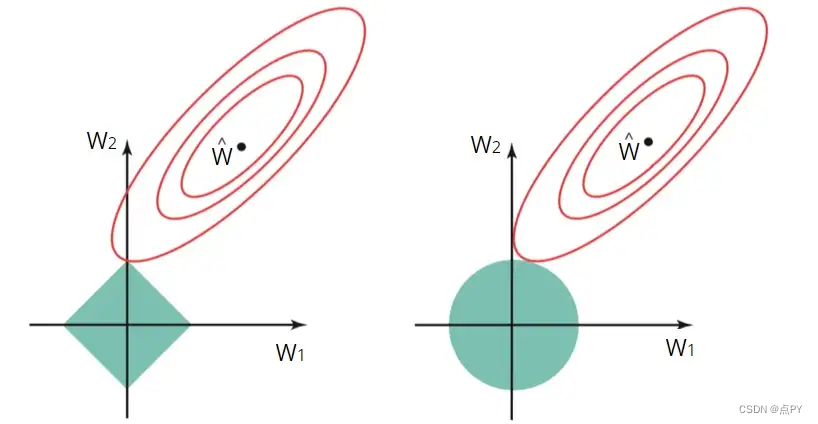
左图显示了 L1 正则化的约束函数（绿色区域），右图显示了 L2 正则化的约束函数。红色椭圆是梯度下降过程中使用的损失函数的轮廓。在等高线的中心有一组最优权重，损失函数具有全局最小值。

在 L1 和 L2 正则化的情况下，W1 和 W2 的估计由椭圆与绿色约束区域相交的第一个点给出。

由于 L2 正则化具有圆形约束区域，交点一般不会出现在轴上，因此 W1 和 W2 的估计值将完全不为零。

在 L1 的情况下，约束区域为带角的菱形。因此，损失函数的轮廓通常会在轴上与约束区域相交。然后发生这种情况，估计值之一（W1 或 W2）将为零。

在高维空间中，许多权重参数将同时为零。

5. 1 Regularization 实现了什么？

• 执行 L2 正则化鼓励权重值趋向于零（但不完全为零）
• 执行 L1 正则化鼓励权重值为零

直观地说，较小的权重会减少隐藏神经元的影响。在那种情况下，那些隐藏的神经元变得可以忽略不计，神经网络的整体复杂性得到降低。

如前所述：不太复杂的模型通常会避免数据中的建模噪声，因此不会出现过度拟合。

但你必须要小心。选择正则化项α 时。目标是在模型的低复杂性和准确性之间取得适当的平衡

• 如果您的 alpha 值太高，您的模型会很简单，但您会面临数据欠拟合的风险。您的模型不会充分了解训练数据以做出有用的预测。
• 如果您的 alpha 值太低，您的模型将更加复杂，并且您将面临过度拟合数据的风险。您的模型将对训练数据的特殊性了解太多，并且无法泛化到新数据。

6. drop out

除了 L2 和 L1 正则化之外，另一种著名且强大的正则化技术称为 dropout 正则化。dropout 正则化背后的过程非常简单。

简而言之，dropout 意味着在以某种概率P进行训练期间，神经网络的神经元在训练期间被关闭。让我们看一个直观的例子。

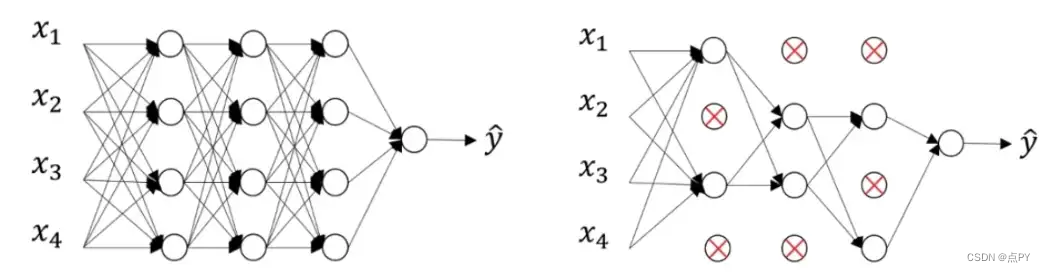
假设在左侧我们有一个没有 dropout 的前馈神经网络。使用 dropout 假设随机神经元在训练期间被关闭的概率P=0.5将导致右侧的神经网络。

在这种情况下，您可以观察到大约一半的神经元不活跃并且不被视为神经网络的一部分。正如您所观察到的，神经网络变得更简单了。

神经网络的更简单版本会降低复杂性，从而减少过度拟合。在每个前向传播和权重更新步骤中应用具有特定概率P的神经元去激活。

7 . 总结

• 过度拟合发生在更复杂的神经网络模型中（很多层，很多神经元）
• 通过使用 L1 和 L2 正则化以及 dropout 可以降低神经网络的复杂性
• L1 正则化强制权重参数变为零
• L2 正则化迫使权重参数趋向于零（但永远不会完全为零）
• 更小的权重参数使一些神经元可以忽略 → 神经网络变得不那么复杂 → 更少的过度拟合
• 在 dropout 期间，一些神经元以随机概率P停用→ 神经网络变得不那么复杂 → 不那么过度拟合