1.前置知识

1.1 Gram-Schmidt正交化

【参考阅读】Gram-Schmidt过程
看完这篇应该基本能理解，但是他对于公式的讲解有一个地方讲解得不是很清楚!

即为什么分母是平方形式呢？

1.2 差集

• 定义：差集是一种集合运算，记A，B是两个集合，则所有属于A且不属于B的元素构成的集合，叫做集合A减集合B(或集合A与集合B之差)，类似地，对于集合A、B，把集合{x∣x∈A，且x∉B}叫做A与B的差集。
• 差集的表示：
  A/B表示A与B的差集
  在论文
  

1.3 SO(n) 特殊正交群

可以自行搜索一下

1.4 stiefel manifold 斯蒂弗尔流形

2. 论文核心内容

神经网络对于分段函数的拟合性并不好

2.1 连续性的表示

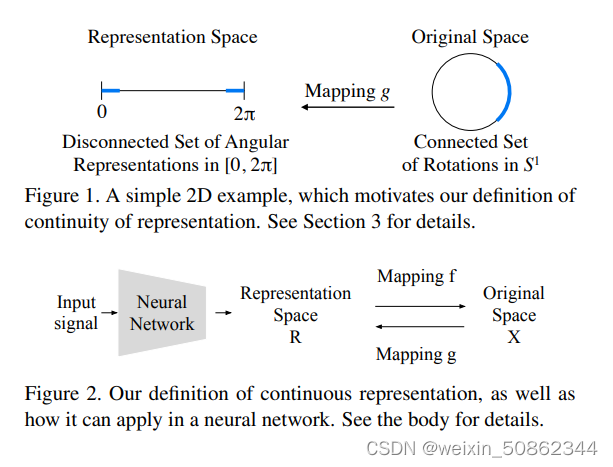
2.2 n2 − n的连续表示方式

2.2.1 连续表示的两个条件

想要使旋转表示是连续的需要满足两个条件

• 恒等映射
• 正交化

2.2.2 从原始空间到表示空间

• （1）定义 表示空间
  使用差集运算，减去表示空间中集合D

集合D：定义为上述类Gram-Schmidt过程不映射回SO（n）的集合：具体来说，这是n的跨度的维度−输入到g的1个矢量小于n− 1.

• 映射关系

从原始空间到表示空间：舍弃最后一个维度

2.2.3 从表示空间到原始空间

一共是3步：

从表示空间到原始空间:


fGS与普通Gram-Schmidt过程的唯一区别在于，最后一列是通过将叉积推广到n维来计算的。

3.1.1

Q:既然原先是正交的,那么为什么舍弃完一个维度之后剩余维度不是正交的呢？
A:舍弃掉最后一个维度之后剩余维度应该仍然

Q2:为什么就从三维变成六维了？
A:表示空间对应是六位的

4. 降维到5维

通过投影