目录

1. INVARIANTS

1.1 例子

1.2 正式的证明

---

1. INVARIANTS

一个不变式需要满足以下三个属性：

1. 当循环开始时，不变式是正确的
2. 在每一次循环迭代之后，不变式仍然是正确的
3. 当循环条件为假时，不变式能推出循环结束后的条件（即后置条件）

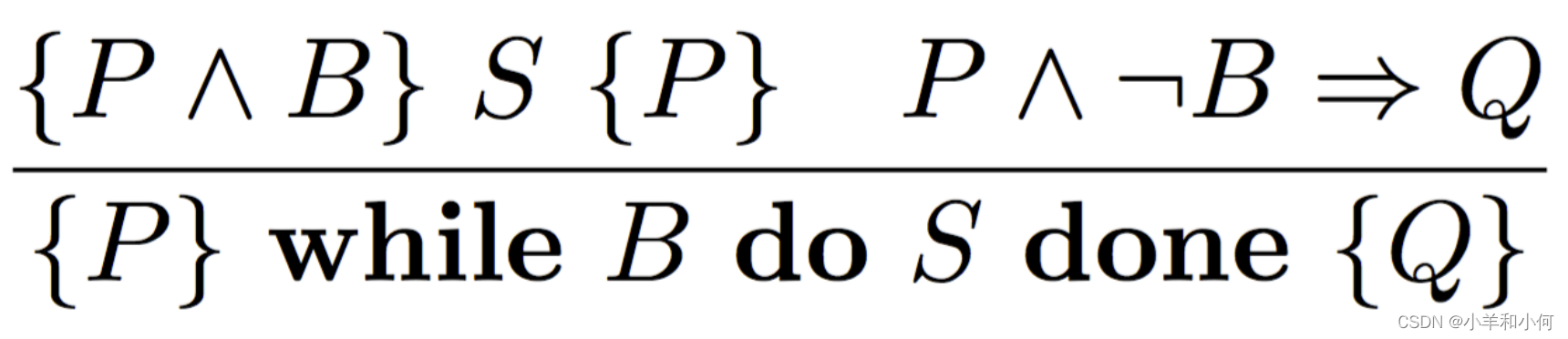
其中循环结构的一般形式表示为：({P ∧B} S {P} P ∧ ¬B => Q) / ({P} while B do S done {Q})，其中P为不变式，B为循环条件，S为循环体中的语句，Q为循环结束后的条件。

1.1 例子

a = A;
result = 0;
while a > 0 do 
  result = result + B; 
  a = a - 1;
done

这个程序计算的是result = A * B。

consequence rules：

 

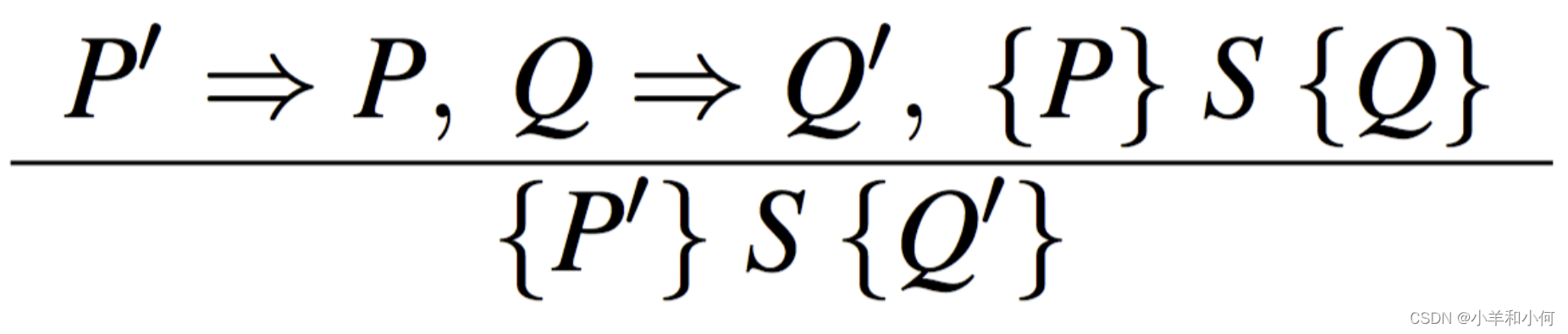
sequence rules：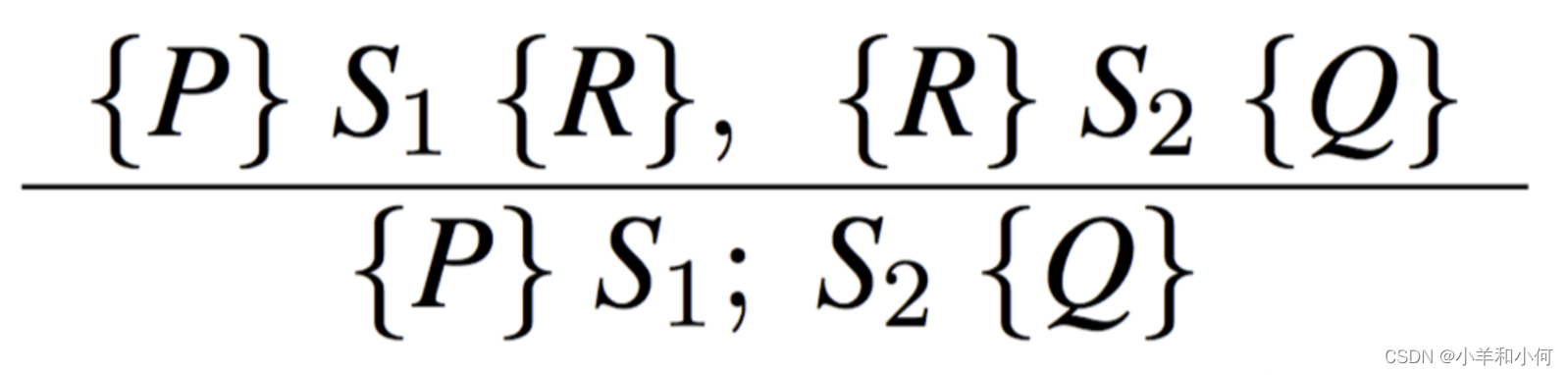

{true}
{?P}
a = A;
{?P1}
result = 0;
{?I}
while a > 0 do 
result = result + B; 
a = a - 1;
done
{result = A * B}

iteration/while loop rule：

 

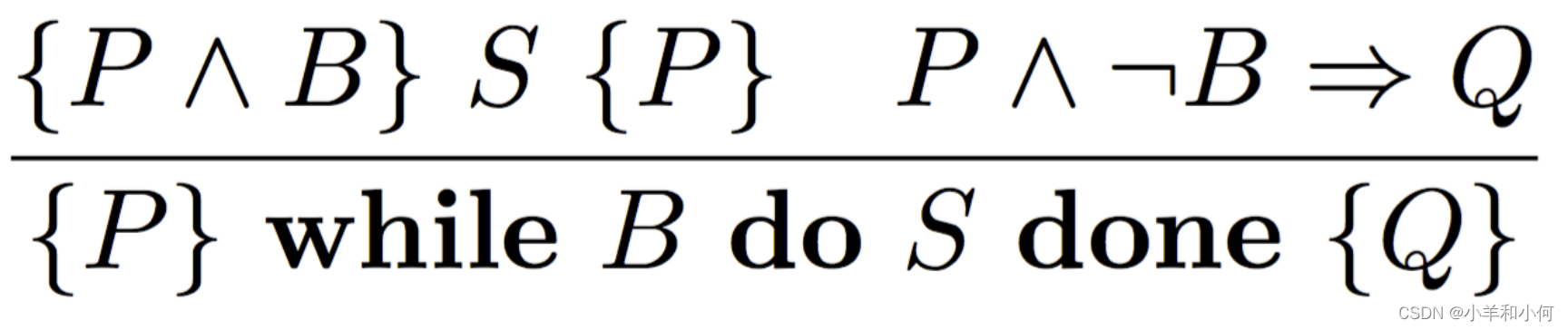
{?I}
while a > 0 do
{?I ∧ a > 0} 
result = result + B;
a = a - 1;
{?I}
done
{?I ∧ a ≤ 0}
{result = A * B}

在用不变式对这个循环结构进行分析时，我们需要找到一个适合的不变式。根据前面说的不变式的性质，我们可以知道，这个不变式通常需要涉及到循环中改变的变量和后置条件中的内容。

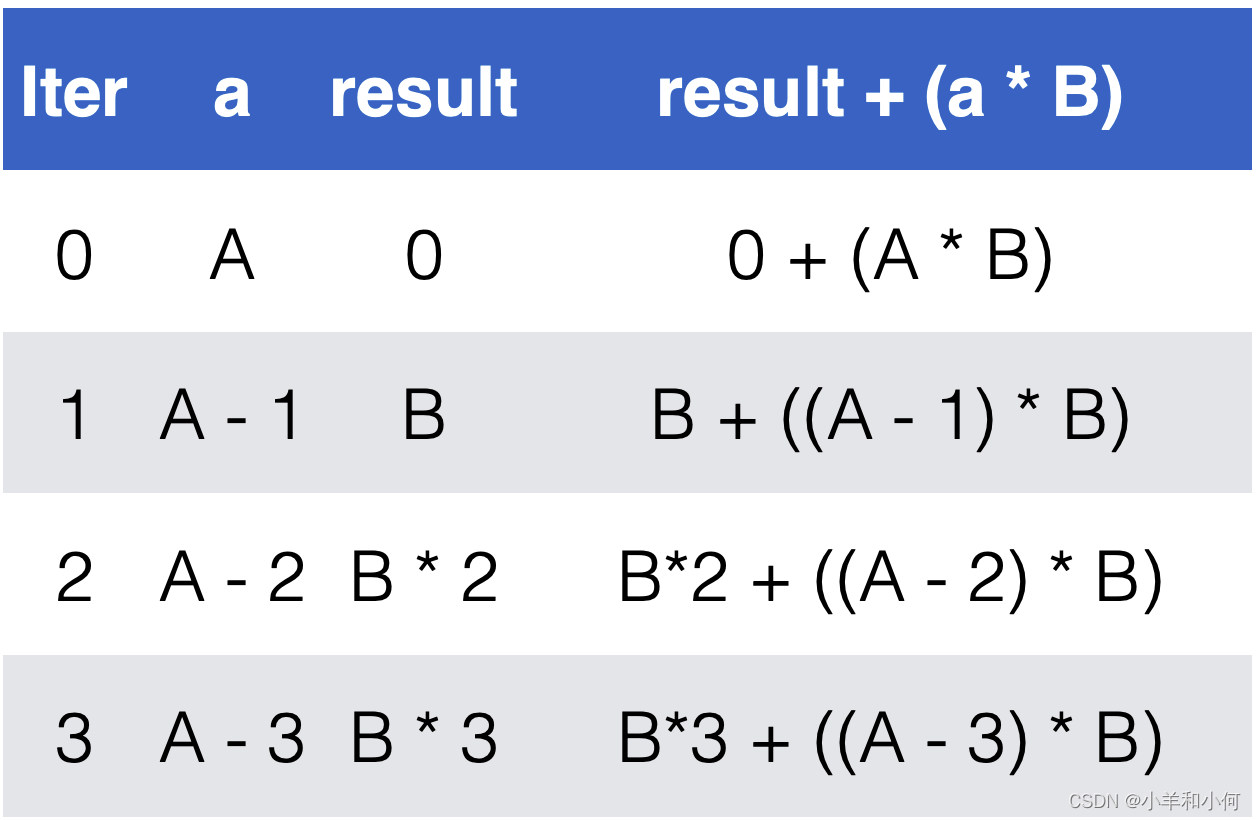
在这个例子中，循环中改变的变量有result和a，后置条件中涉及到的变量有A和B。根据这些变量，我们可以得到一个可能的不变式：result + (a * B) = A * B。

我们观察到每次迭代，result 增加 B，而 a 减1。所以我们可以选择 result + a * B = A * B 作为我们的循环不变量。

接下来，我们可以验证这个不变式是否满足不变式的性质：

1. 当循环开始时，a的值是A，result的值是0，所以result + (a * B) = 0 + (A * B) = A * B，满足不变式。
2. 在每一次循环迭代之后，result增加B，a减1，所以result + (a * B)的值没有变化，仍然等于A * B，满足不变式。
3. 当a变为0时，result的值变为A * B，所以result + (a * B) = result + 0 = A * B，满足后置条件。

因此，我们可以确认这个不变式是正确的。这个不变式也帮助我们理解了这个程序的功能：它实现的是一个乘法运算，其中的循环就是不断地做加法运算来实现乘法。

1.2 正式的证明

这里有两个关键目标：

1. 在循环开始时和每一次循环之后，我们需要证明不变式（Invariant）result + (a * B) = A * B是正确的。

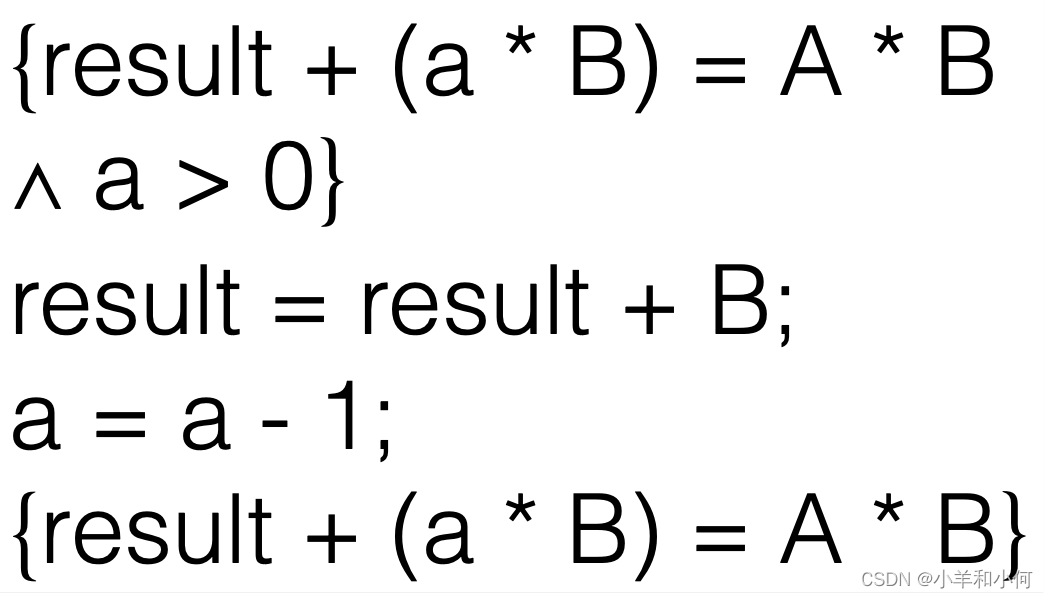
1. 在循环结束时（即a不大于0时），我们需要证明result = A * B。

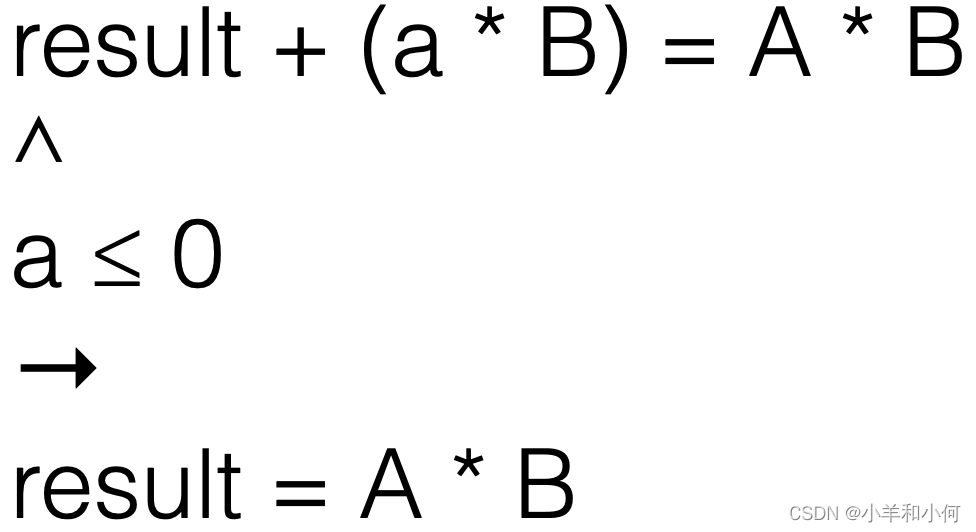
目标1在早前的幻灯片中已经完成。对于目标1，我们可以发现，如果我们只使用result + (a * B) = A * B这个不变式，并不能推导出result = A * B。因为当a小于等于0时，它可能是负数，而在这个程序中，a应当是非负的。

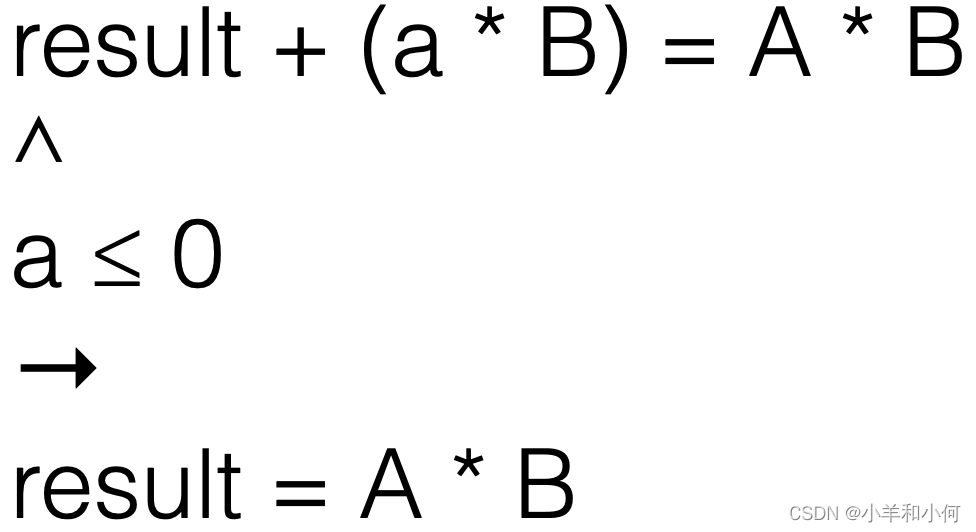
因此，我们需要将不变式加强，包括条件a ≥ 0。所以，新的不变式变为result + (a * B) = A * B ∧ a ≥ 0。

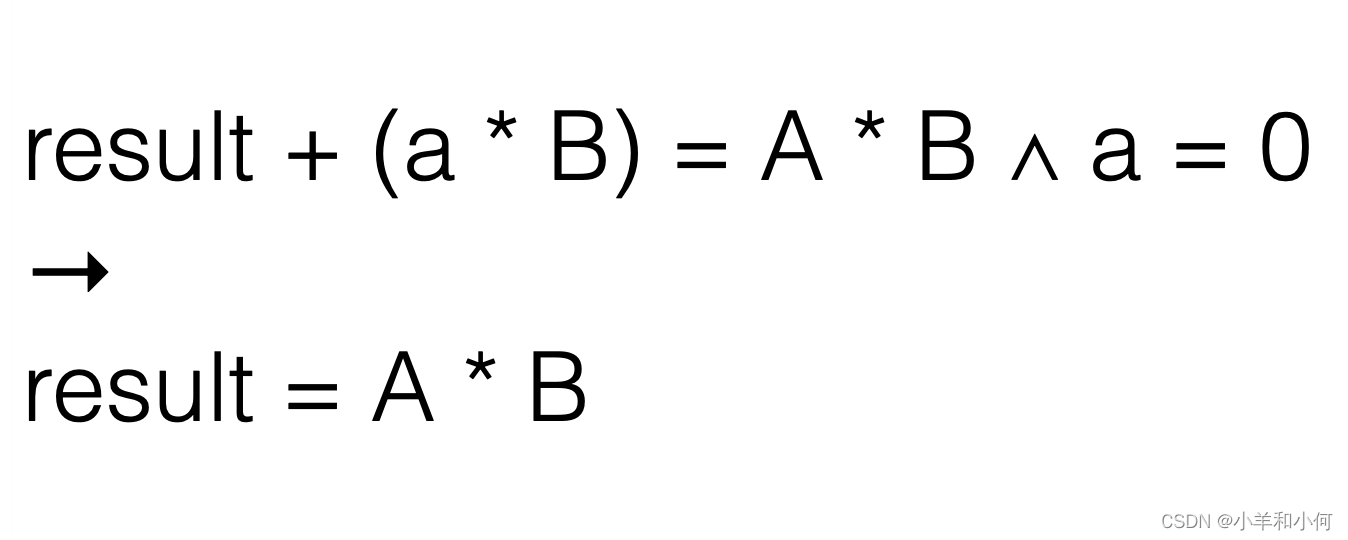
接下来，我们进行两个目标的证明：

目标1（循环结束时）：我们需要证明result + (a * B) = A * B ∧ a = 0能够推导出result = A * B。这个显然是正确的，当a = 0时，result = A * B。

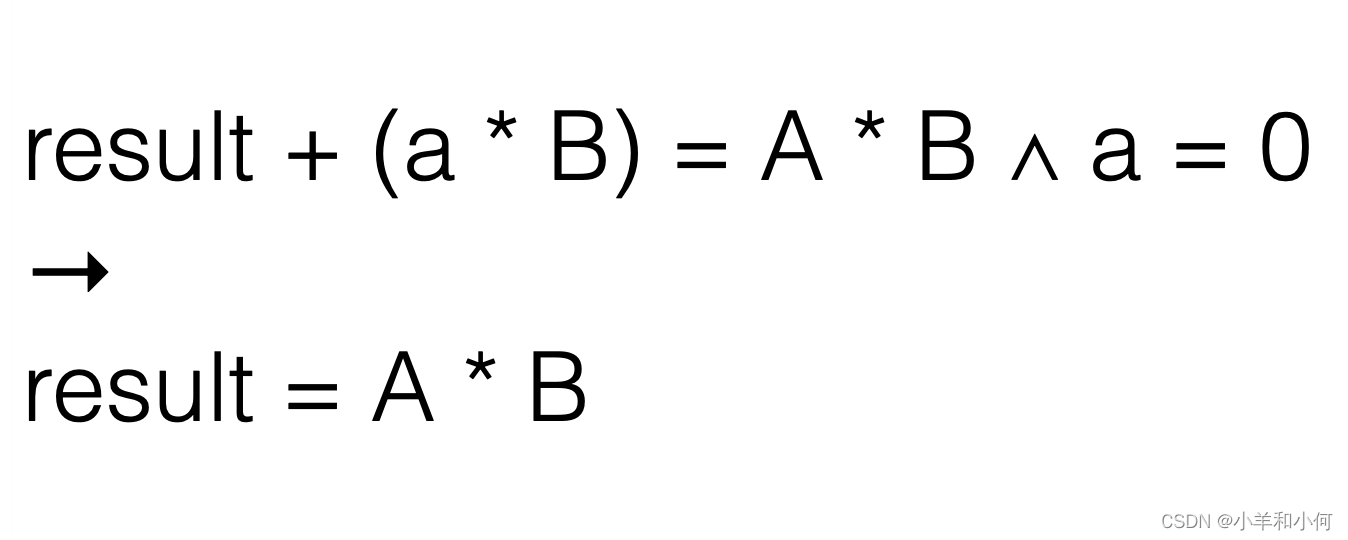
目标2（循环中）：我们需要证明，给定result + (a * B) = A * B ∧ a > 0，执行一次循环后（result = result + B; a = a - 1;），仍能保持不变式result + (a * B) = A * B ∧ a ≥ 0。

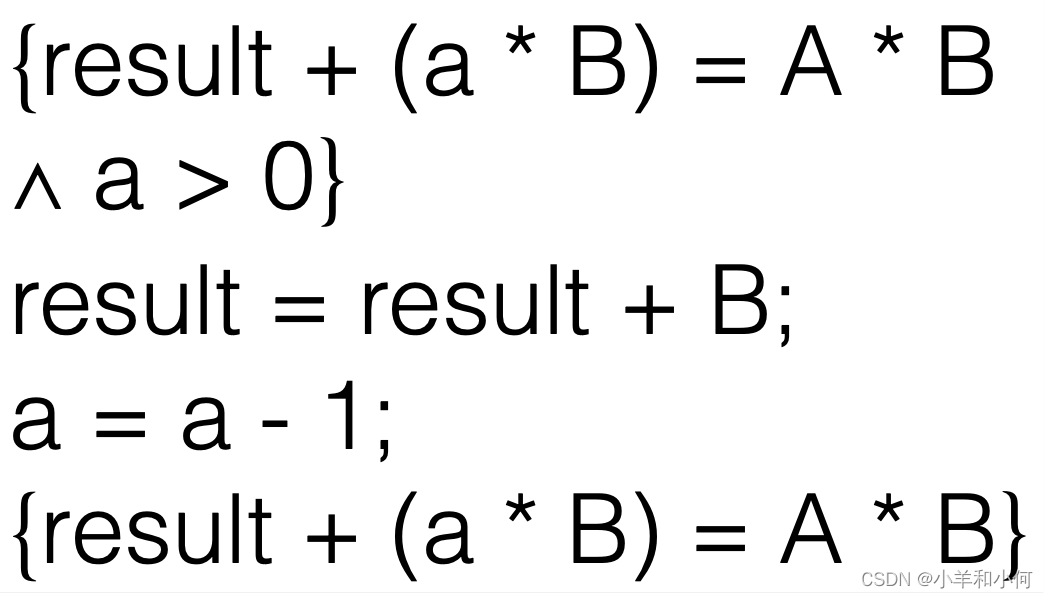
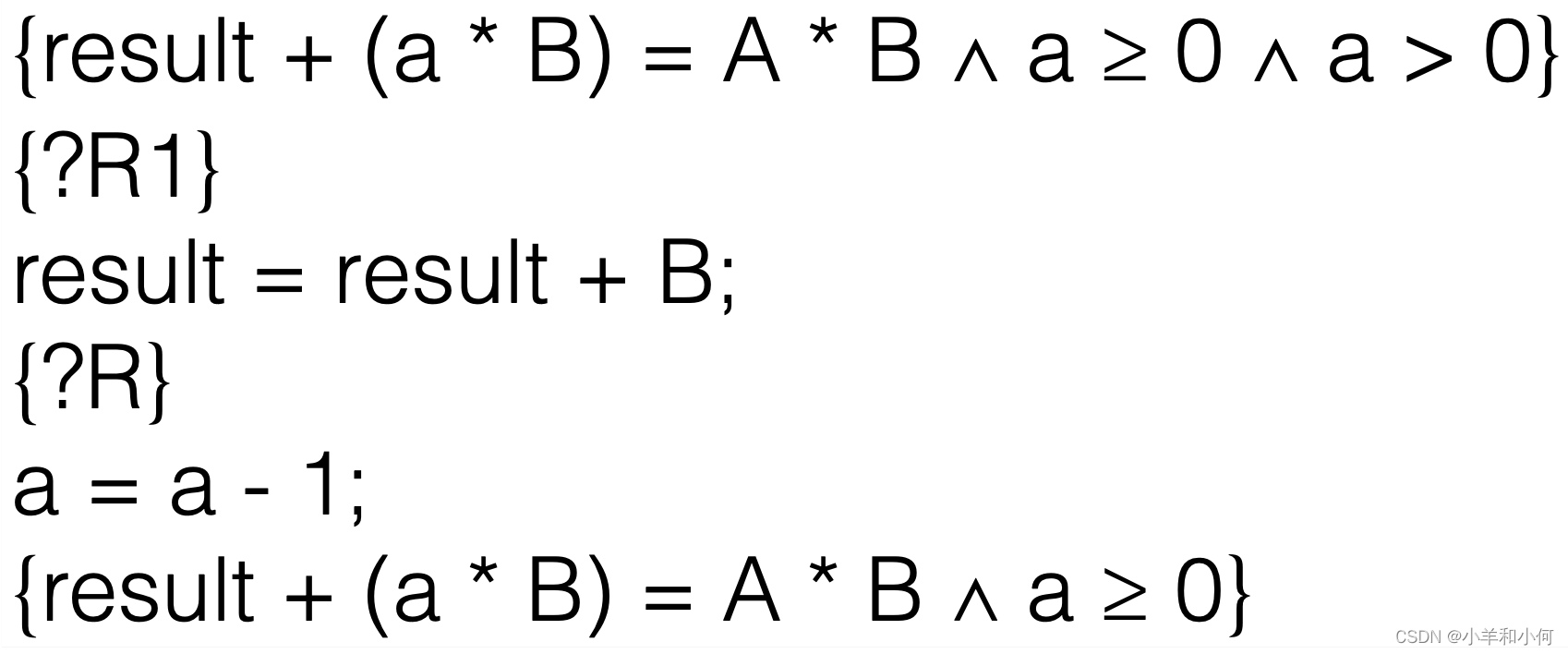
将待证明的整个过程分成两个小步骤，每一步都有一个中间条件?R1和?R。

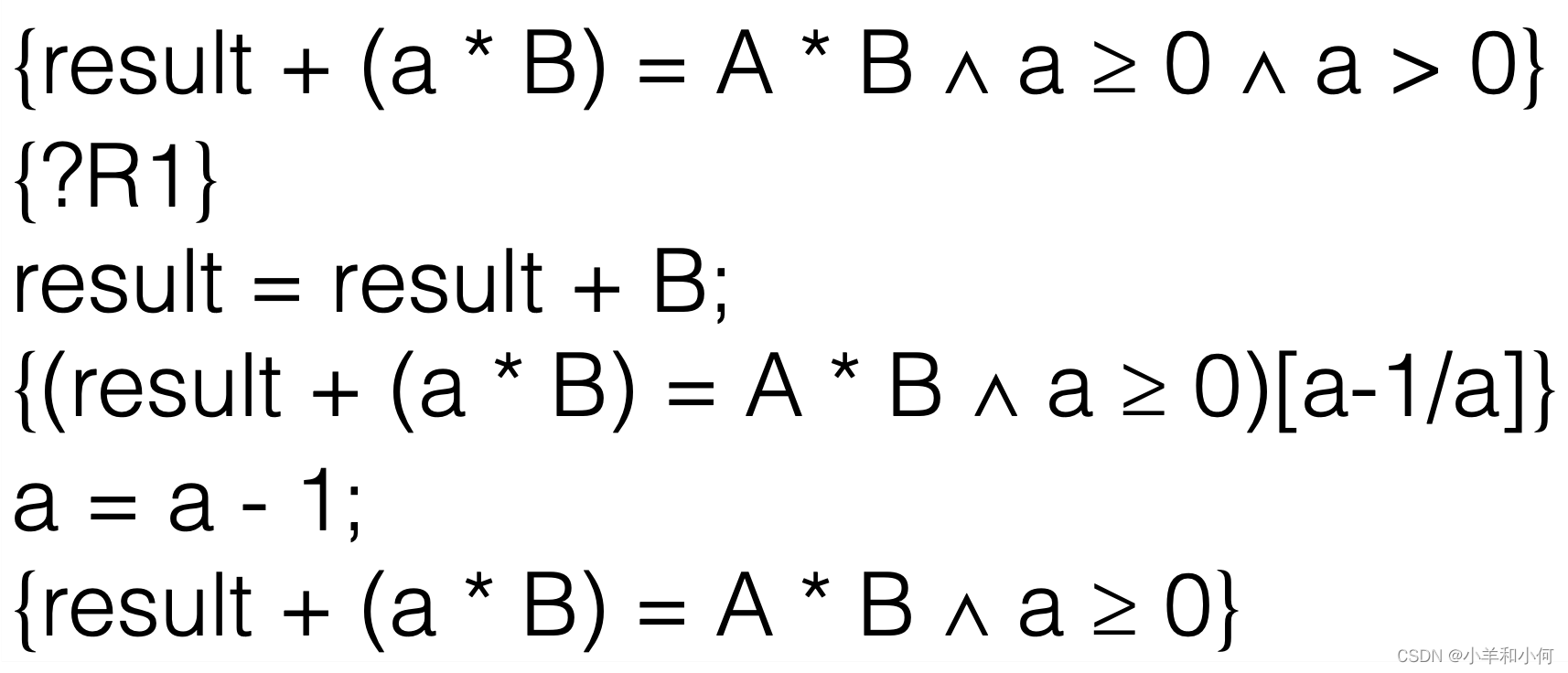
使用霍尔逻辑的赋值规则（Assignment Rule）来找出?R。赋值规则说，如果你有一个赋值x := E和一个后置条件P，那么前置条件是P[E/x]。这里，我们将a - 1替换a。

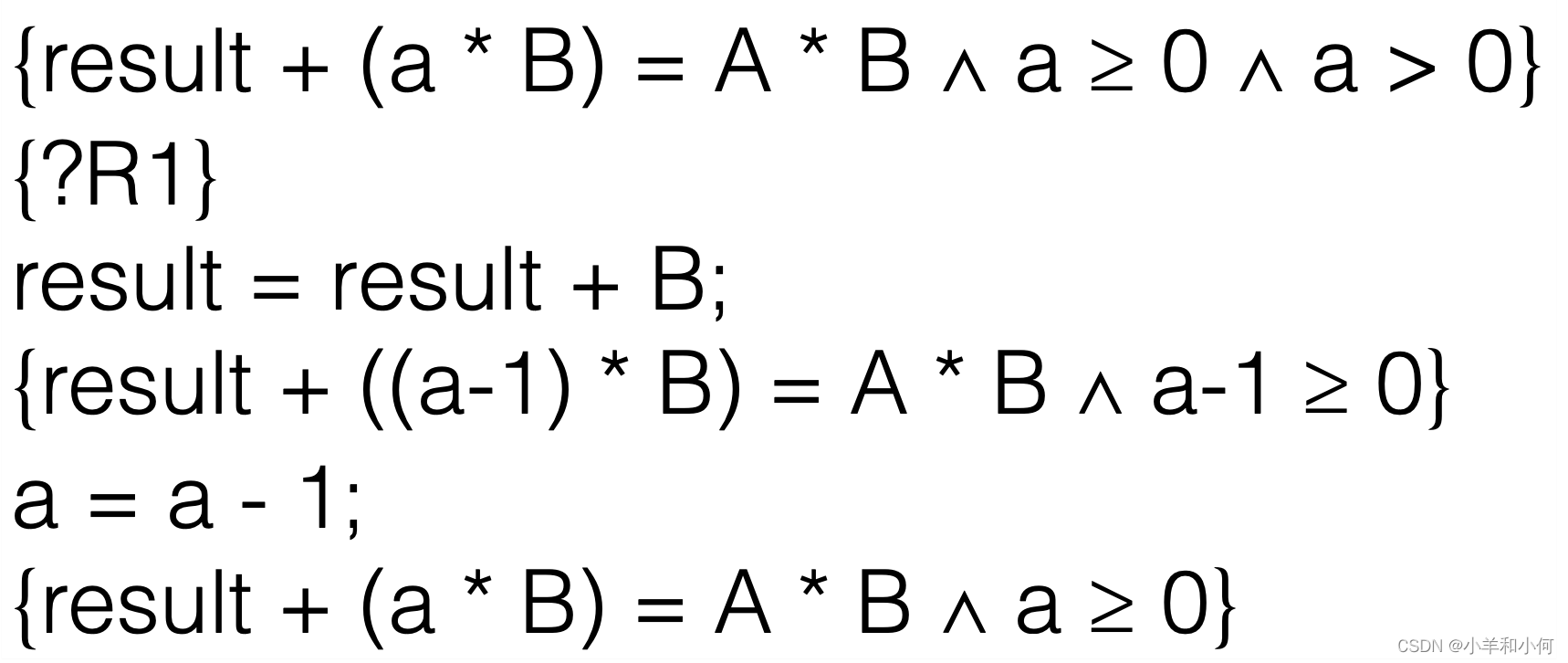
在前置条件中完成替换。

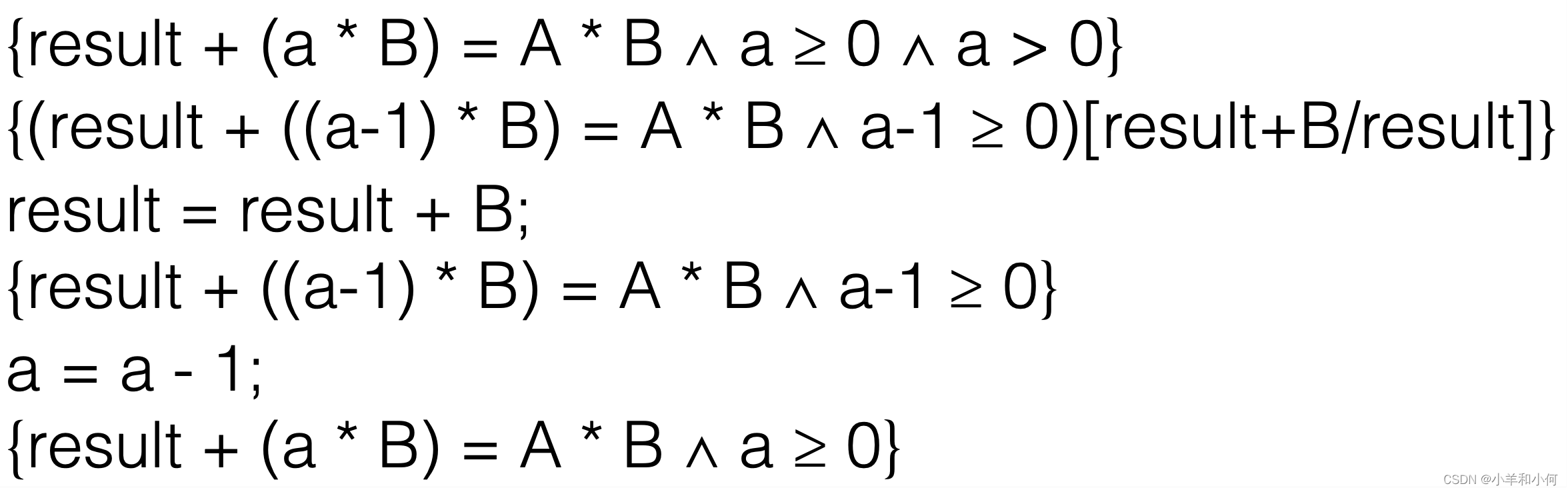
同样，使用赋值规则来找出?R1。这次，我们将result + B替换result。

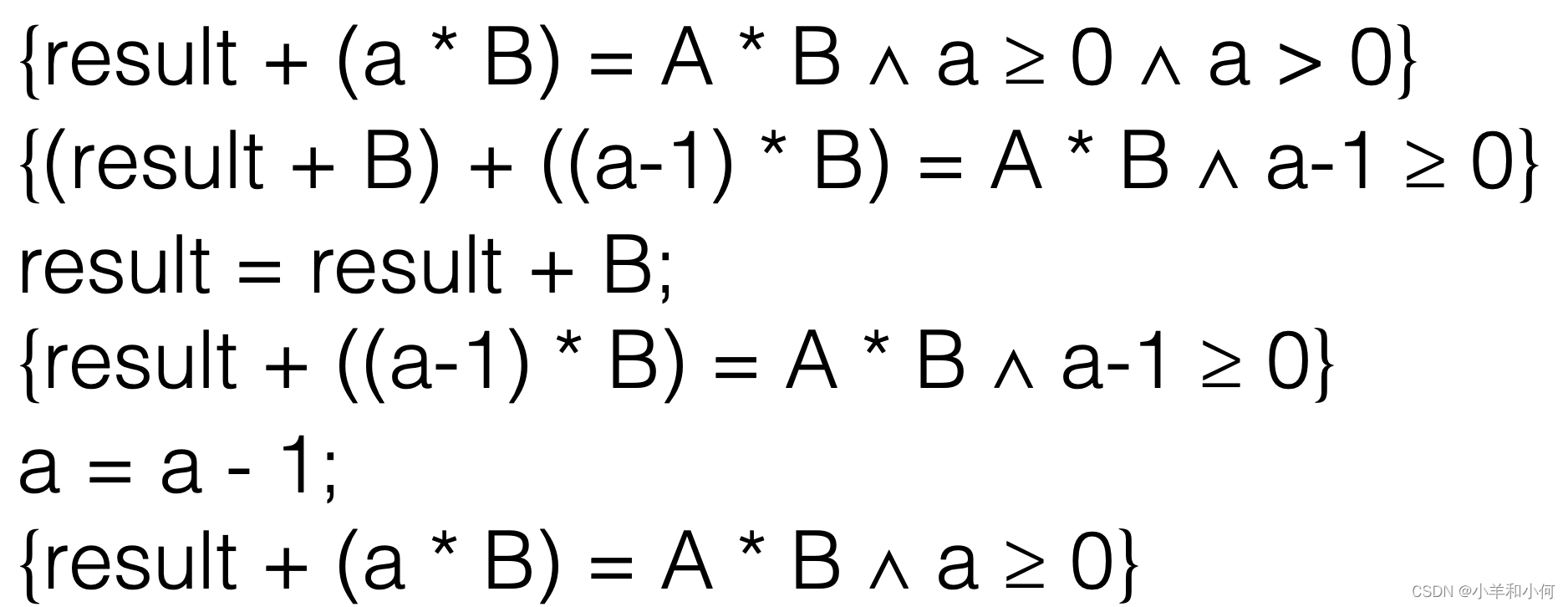
在前置条件中完成替换。 

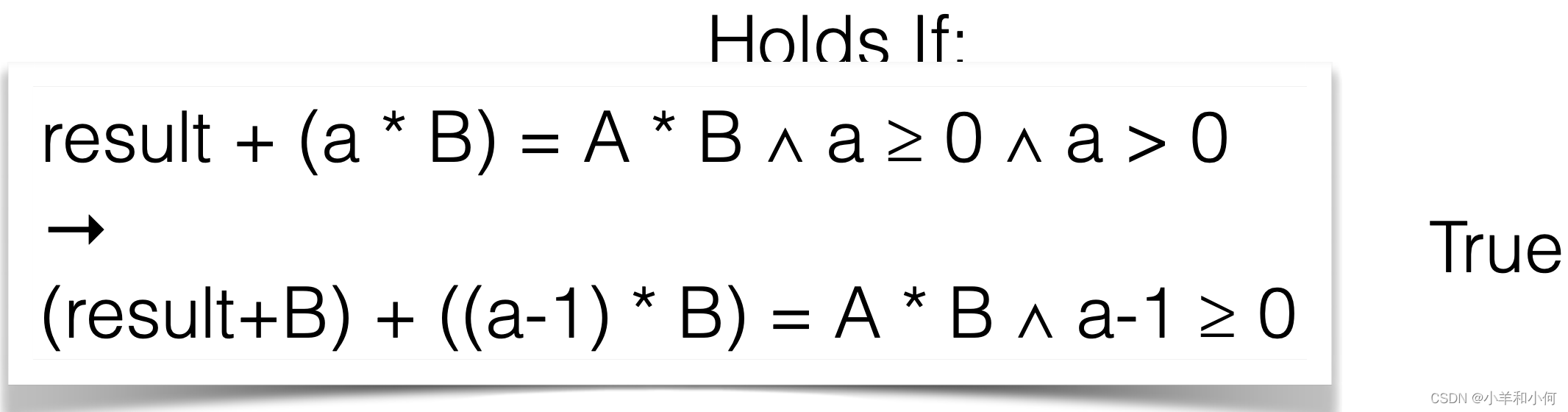
Holds If：这一部分是在检查步骤5得到的前置条件是否能够由原前置条件推导出。在这里，显然是可以的。

Rest of the Program

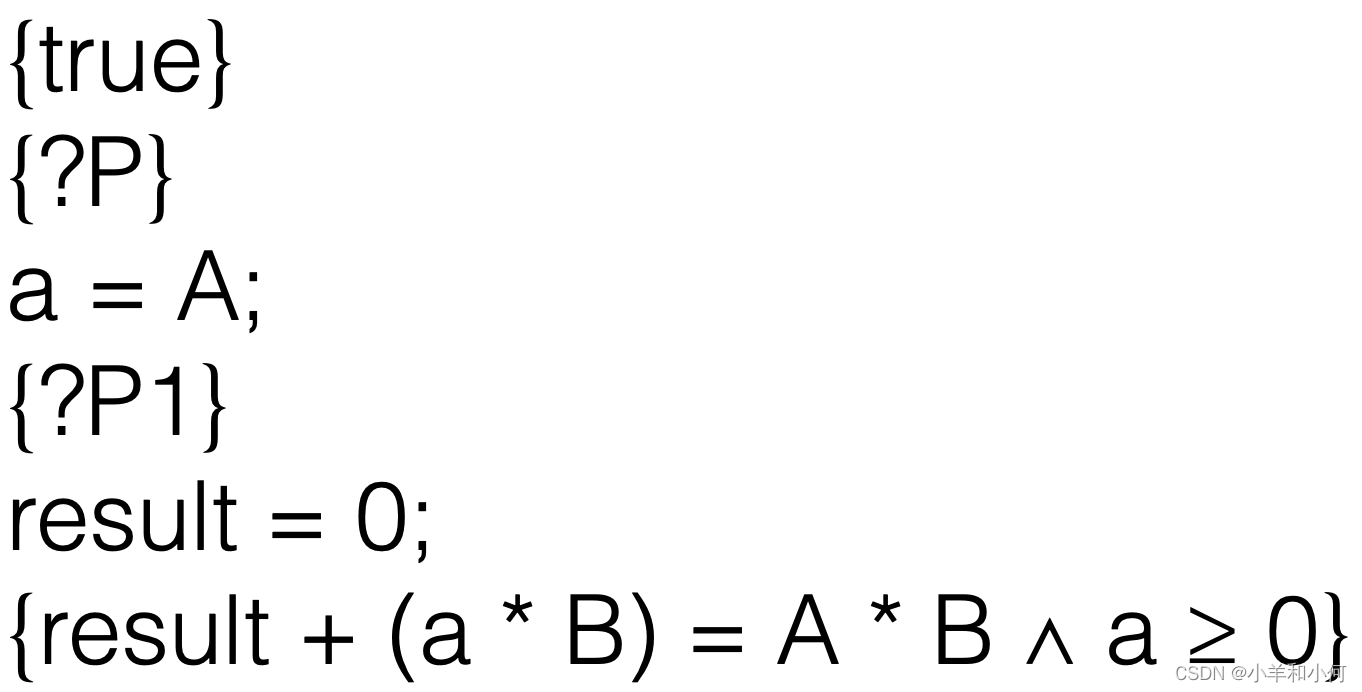
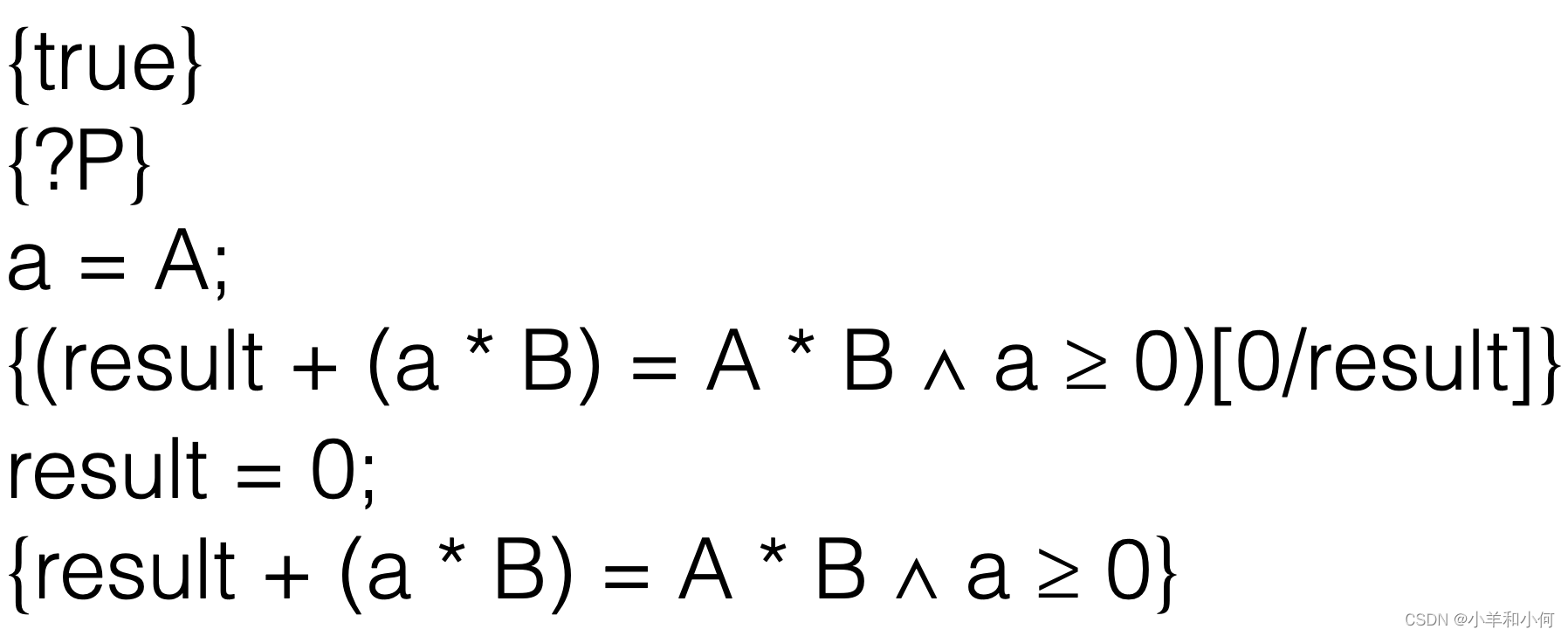
同理，这些步骤都在找出每一步的前置条件。唯一不同的是，这里的目标是找出整个程序的前置条件，而不仅仅是循环部分。 

 

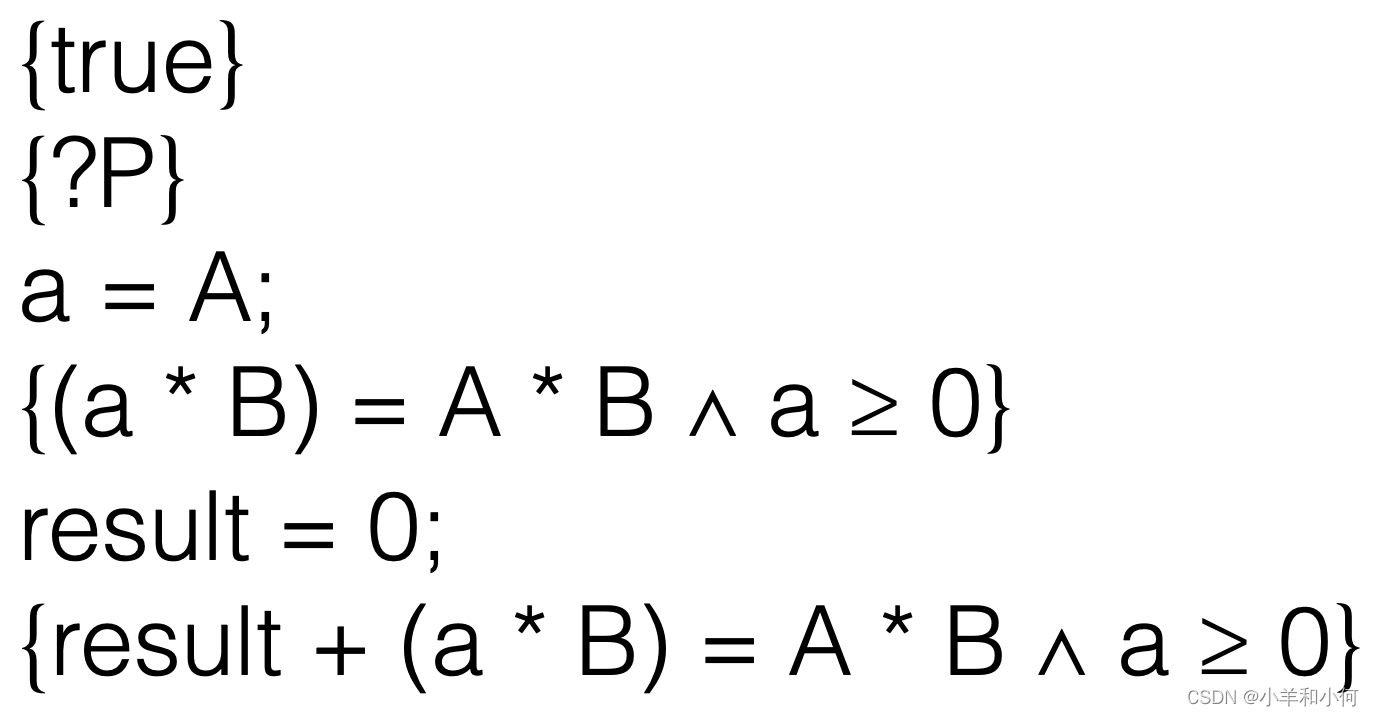
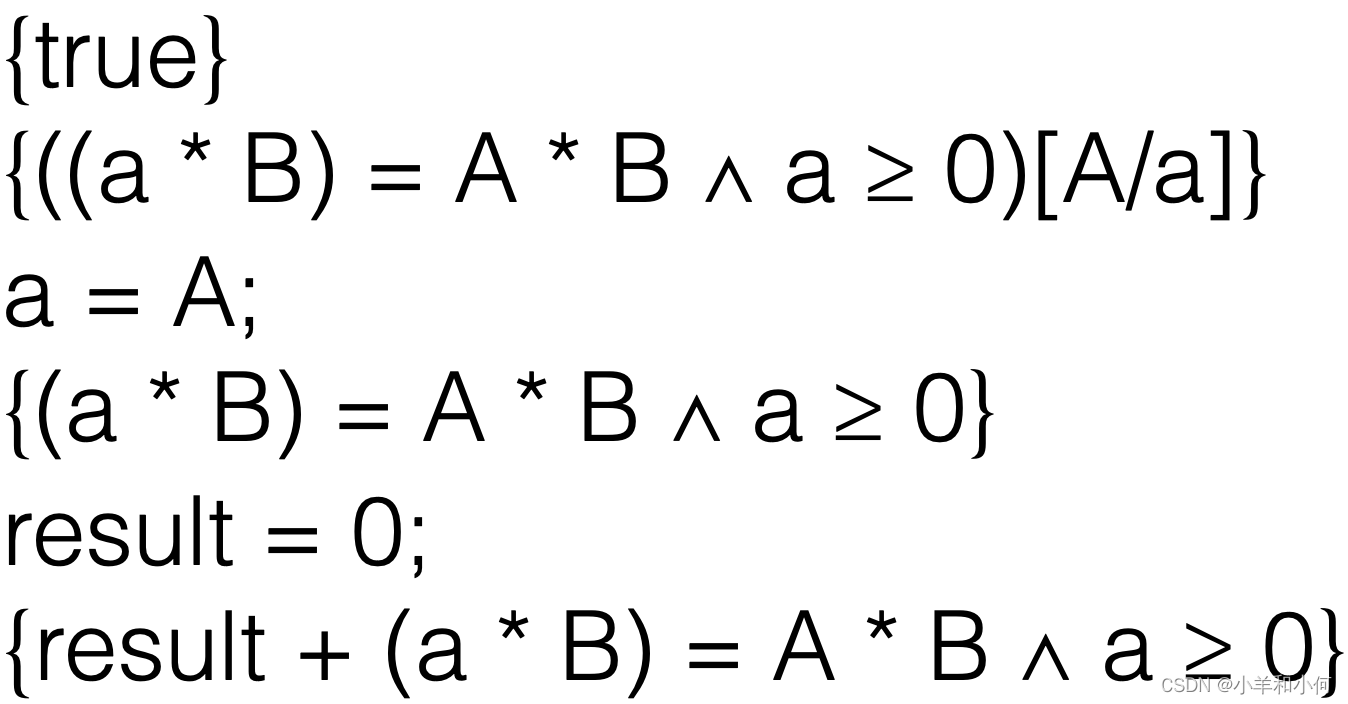
这一步是在处理赋值a = A。同样，我们使用赋值规则，将A替换a。

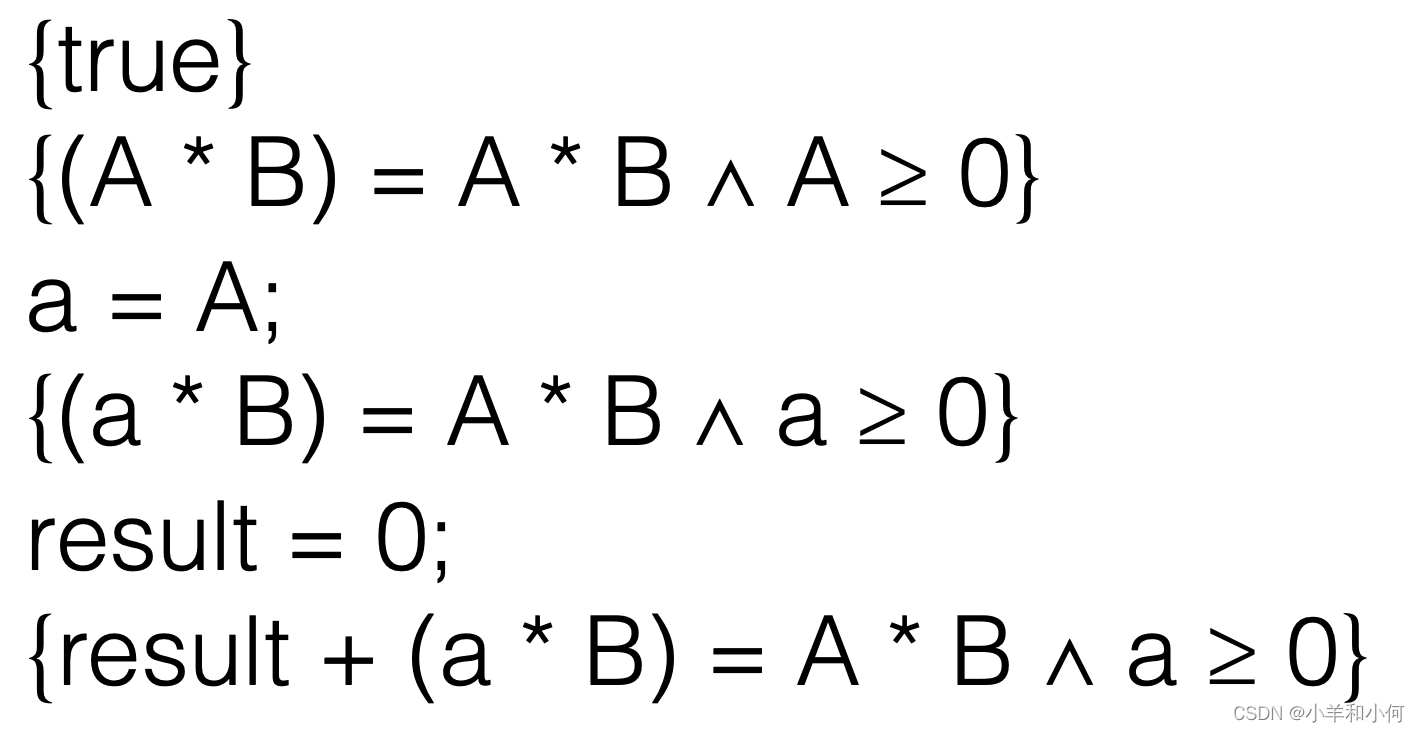
在前置条件中完成替换。

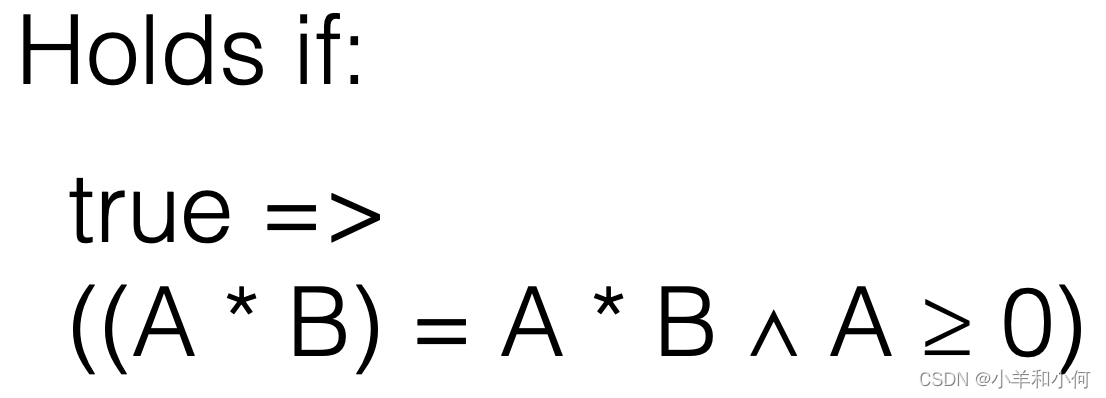
Holds If：这一部分是在检查步骤11得到的前置条件是否能够由原前置条件推导出。在这里，我们发现，如果A小于0，那么前置条件并不能得到满足，所以我们得出结论：这个推导不成立。

Strengthen Precondition

 因为上一步的结果，我们需要加强前置条件，保证A ≥ 0。

在前置条件中添加了新的条件。

这是一个完整的霍尔逻辑证明，包括前置条件、后置条件、以及循环的不变式。在这一步，我们得出了最终的结论：在前置条件A ≥ 0下，这个程序能够正确计算result = A * B。

这部分的证明包含了一些较复杂的代换和推导，核心的证明步骤是：首先按照程序的执行，将result和a的值进行更新；然后，证明更新后的表达式仍满足不变式。这里的关键是，不变式中的result增加了B，而a减小了1，所以result + (a * B)的值并没有改变。

然后，我们检查这个循环程序的前置条件。我们发现，当A小于0时，前置条件并不满足。因此，我们需要加强前置条件，确保A ≥ 0。

最后，我们得到了完整的循环程序和它的霍尔逻辑表示：

{A ≥ 0}
a = A;
result = 0;
while a > 0 do 
  result = result + B; 
  a = a - 1;
done
{result = A * B}

其中，不变式（Invariant）是result + (a * B) = A * B ∧ a ≥ 0。通过这个不变式，我们可以保证在循环开始、循环中、循环结束时，程序的状态都满足我们的期望，从而证明了这个循环程序的正确性。