贝塞尔曲线的绘制
由于 CSDN 的博客修改字数的限制,我们不得不将这一部分放到一个新的博客中。原文详见:
GGN_2015
计算机图形学中的曲线问题
贝塞尔曲线的几何作图法
在上面介绍儿时的回忆中,我们介绍了对于抛物线绘制的一种方法。如下图所示,我们要先选定三个控制点
A
,
B
,
C
A, B, C
A,B,C,连接
A
B
AB
AB、
B
C
BC
BC。我们在
A
B
AB
AB 上取一点
D
D
D,在
B
C
BC
BC 上取一点
E
E
E 使得:
A
D
A
B
=
B
E
B
C
=
t
\frac {AD}{AB}=\frac{BE}{BC}=t
ABAD=BCBE=t
其中
t
t
t 是一个定义在
[
0
,
1
]
[0, 1]
[0,1] 区间上的数。之后我们再连接
D
E
DE
DE 并在
D
E
DE
DE 上取一点
F
F
F 使得:
D
F
D
E
=
t
\frac{DF}{DE}=t
DEDF=t
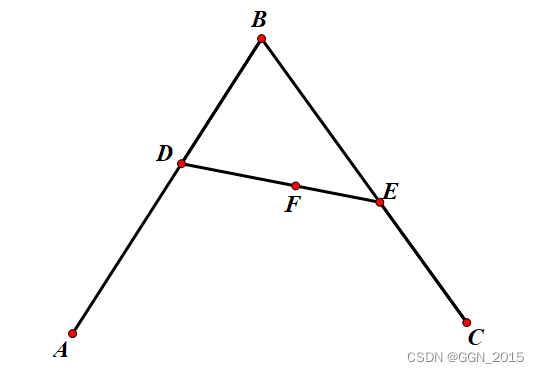
当 t t t 在 [ 0 , 1 ] [0, 1] [0,1] 之间变化时, F F F 点的轨迹就是一条抛物线(换言之,二次贝塞尔曲线)。当 t t t 变化时,点 F F F 的运动效果如下:
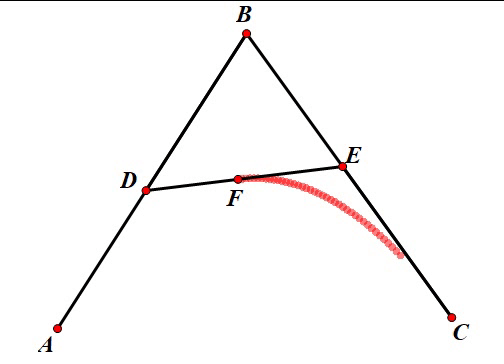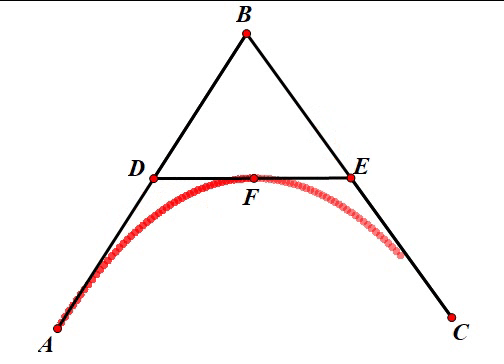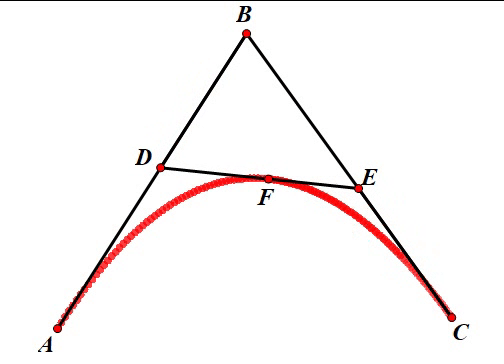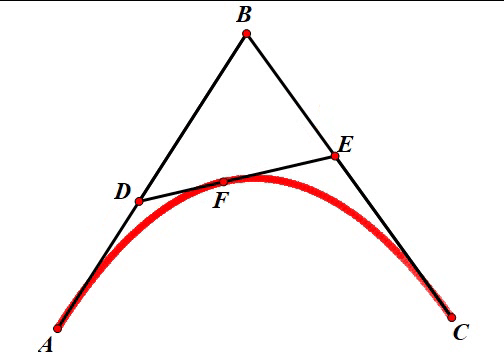
对于三次贝塞尔曲线我们也可以使用同样的方法进行绘制,只不过这次控制点的个数要增加到四个。先取四个控制点
A
,
B
,
C
,
D
A, B, C, D
A,B,C,D,分别连接
A
B
AB
AB,
B
C
BC
BC,
C
D
CD
CD,使用同样的比例
t
t
t 在这三个线段上各取一点,记为
E
,
F
,
G
E, F, G
E,F,G。连接
E
F
EF
EF 和
F
G
FG
FG,再使用相同的比例
t
t
t 在这两条线段上分别取一点,记为
J
,
K
J, K
J,K。最后,连接
J
K
JK
JK,在线段
J
K
JK
JK 上按照比例
t
t
t 取一点
M
M
M。在
t
t
t 变化的过程中,
M
M
M 点的运动轨迹就是一条三次贝塞尔曲线。
相同的比例指:
A
E
A
B
=
B
F
B
C
=
C
G
C
D
=
E
J
E
F
=
F
K
F
G
=
J
M
J
K
=
t
\frac{AE}{AB}=\frac{BF}{BC}=\frac{CG}{CD}=\frac{EJ}{EF}=\frac{FK}{FG}=\frac{JM}{JK}=t
ABAE=BCBF=CDCG=EFEJ=FGFK=JKJM=t
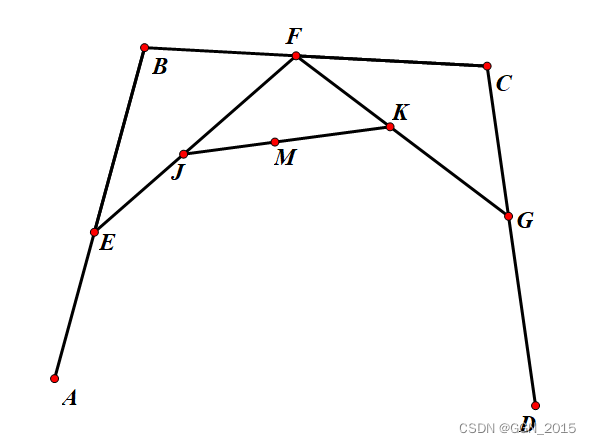
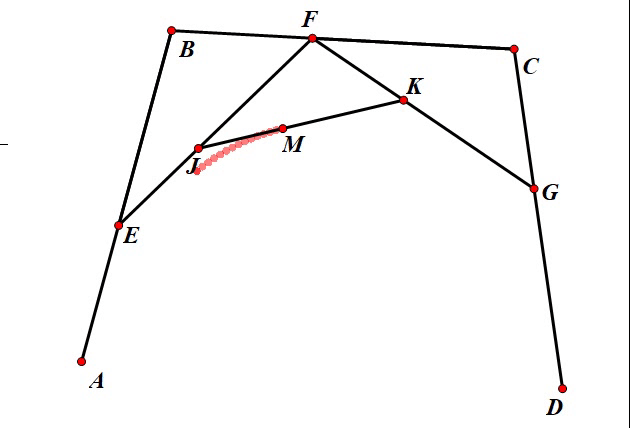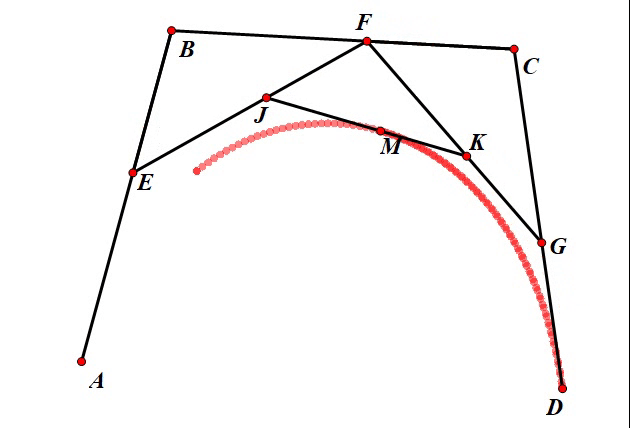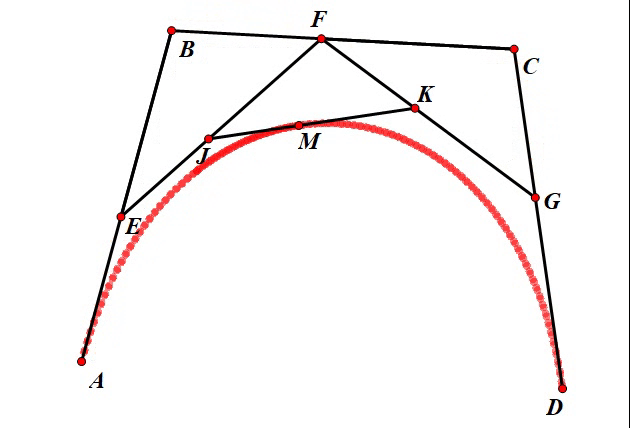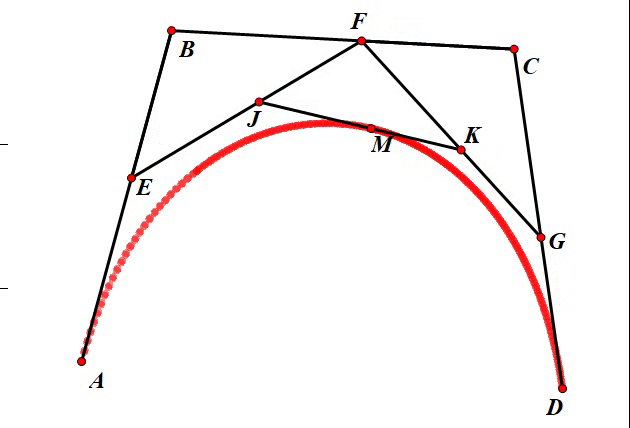
这个关系虽然看起来比较繁琐,但实际上并不复杂。可以看到在这个三次贝塞尔曲线的几何作图法表述中,点 J J J 和点 K K K 各自运动的轨迹就是一条二次的贝塞尔曲线,而点 M M M 的运动轨迹是一条三次贝塞尔曲线,因此,我们可以说三次贝塞尔曲线是对两条二次贝塞尔曲线的“合并”。运动效果如下:
设
J
J
J 点的运动方程为
f
1
(
t
)
,
t
∈
[
0
,
1
]
f_1(t), t\in[0, 1]
f1(t),t∈[0,1],
K
K
K 点的运动方程为
f
2
(
t
)
,
t
∈
[
0
,
1
]
f_2(t), t\in[0, 1]
f2(t),t∈[0,1],则
M
M
M 点的运动方程为
f
3
(
t
)
=
(
1
−
t
)
⋅
f
1
(
t
)
+
t
⋅
f
2
(
t
)
f_3(t)=(1-t)\cdot f_1(t)+t\cdot f_2(t)
f3(t)=(1−t)⋅f1(t)+t⋅f2(t) 。这种合并会使得曲线
f
3
f_3
f3 的前半段比较接近
f
1
f_1
f1,后半段比较接近
f
2
f_2
f2。下图中的绿线和蓝线分别是
f
1
f_1
f1 和
f
2
f_2
f2,红线是
f
3
f_3
f3。
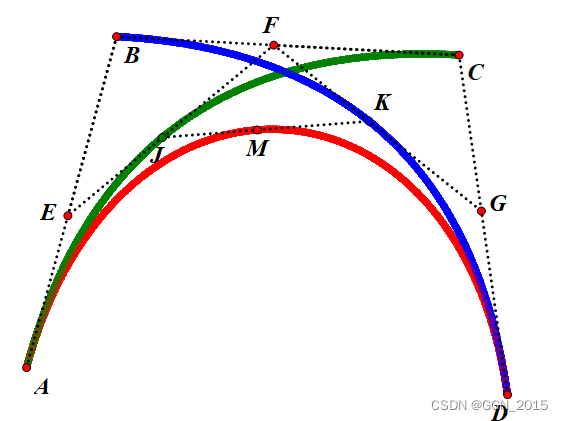
为了表述方便,我们称:折线
A
B
C
D
ABCD
ABCD 是红色曲线
f
3
f_3
f3 的控制多边形。
贝塞尔曲线的分裂法绘制
根据文章正文中的介绍我们已经得知,如果
A
B
C
D
ABCD
ABCD 是曲线
f
3
f_3
f3 的控制多边形,那么有:
f
3
(
t
)
=
(
1
−
t
)
3
⋅
A
+
3
(
1
−
t
)
2
t
⋅
B
+
3
(
1
−
t
)
t
2
⋅
C
+
t
3
⋅
D
,
t
∈
[
0
,
1
]
f_3(t)=(1-t)^3\cdot A+3(1-t)^2t\cdot B+3(1-t)t^2\cdot C+t^3 \cdot D, t\in[0, 1]
f3(t)=(1−t)3⋅A+3(1−t)2t⋅B+3(1−t)t2⋅C+t3⋅D,t∈[0,1]
在 t t t 变化的过程中,我们可以观察到,当 t → 0 t\to 0 t→0 时, A E J M AEJM AEJM 四点几乎接近左半段曲线,当 t → 1 t\to 1 t→1 时, M K G D MKGD MKGD 几乎接近右半段曲线,而这种性质中似乎暗含着一些不可告人的秘密。正如 A B C D ABCD ABCD 是整段曲线 f 3 f_3 f3 的控制多边形,我们有理由猜测: A E J M AEJM AEJM 是否是 f 3 f_3 f3 在 M M M 左侧部分的曲线的控制多边形而 M K G D MKGD MKGD 是 f 3 f_3 f3 在 M M M 右侧部分的控制多边形呢?
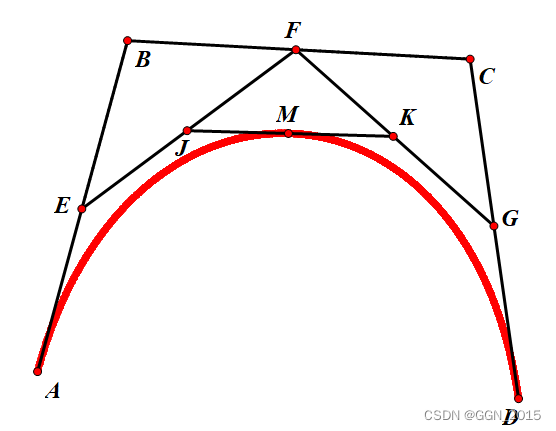
假设当前
t
=
1
2
t=\frac 1 2
t=21,那么我们可以算出
E
,
J
,
M
E, J, M
E,J,M 三点各自的坐标:
E
=
(
1
−
t
)
⋅
A
+
t
⋅
B
=
A
+
B
2
F
=
(
1
−
t
)
⋅
B
+
t
⋅
C
=
B
+
C
2
G
=
(
1
−
t
)
⋅
C
+
t
⋅
D
=
C
+
D
2
J
=
(
1
−
t
)
⋅
E
+
t
⋅
F
=
A
+
2
B
+
C
4
K
=
(
1
−
t
)
⋅
F
+
t
⋅
G
=
B
+
2
C
+
D
4
M
=
A
+
3
B
+
3
C
+
D
8
\begin{aligned} E&=(1-t)\cdot A+t\cdot B=\frac{A+B}{2}\\ F&=(1-t)\cdot B+t\cdot C=\frac{B+C}{2}\\ G&=(1-t)\cdot C+t\cdot D=\frac{C+D}{2}\\ J&=(1-t)\cdot E+t\cdot F=\frac{A+2B+C}{4}\\ K&=(1-t)\cdot F+t\cdot G=\frac{B+2C+D}{4}\\ M&=\frac{A+3B+3C+D}{8} \end{aligned}
EFGJKM=(1−t)⋅A+t⋅B=2A+B=(1−t)⋅B+t⋅C=2B+C=(1−t)⋅C+t⋅D=2C+D=(1−t)⋅E+t⋅F=4A+2B+C=(1−t)⋅F+t⋅G=4B+2C+D=8A+3B+3C+D
我们定义
A
E
J
M
AEJM
AEJM 四个点确定的三次贝塞尔曲线为
f
(
t
)
f(t)
f(t),则有:
f
(
t
)
=
(
1
−
t
)
3
⋅
A
+
3
(
1
−
t
)
2
t
⋅
E
+
3
(
1
−
t
)
t
2
⋅
J
+
t
3
⋅
M
,
t
∈
[
0
,
1
]
f(t)=(1-t)^3\cdot A+3(1-t)^2t\cdot E+3(1-t)t^2\cdot J+t^3 \cdot M, t\in[0, 1]
f(t)=(1−t)3⋅A+3(1−t)2t⋅E+3(1−t)t2⋅J+t3⋅M,t∈[0,1]
我们不妨把上式整理成只含有
A
B
C
D
ABCD
ABCD 四个点的形式:
f
(
t
)
=
(
1
−
t
)
3
⋅
A
+
3
(
1
−
t
)
2
t
⋅
A
+
B
2
+
3
(
1
−
t
)
t
2
⋅
A
+
2
B
+
C
4
+
t
3
⋅
A
+
3
B
+
3
C
+
D
8
,
t
∈
[
0
,
1
]
=
(
A
B
C
D
)
×
[
1
1
2
1
4
1
8
0
1
2
2
4
3
8
0
0
1
4
3
8
0
0
0
1
8
]
×
(
(
1
−
t
)
3
3
(
1
−
t
)
2
t
3
(
1
−
t
)
t
2
t
3
)
,
t
∈
[
0
,
1
]
\begin{aligned} f(t)&=(1-t)^3\cdot A+3(1-t)^2t\cdot \frac{A+B}{2}+3(1-t)t^2\cdot \frac{A+2B+C}{4}+t^3 \cdot \frac{A+3B+3C+D}{8}, t\in[0, 1]\\ &=\left(\begin{matrix}A&B&C&D \end{matrix}\right)\times\left[\begin{matrix}1&\frac 1 2 & \frac 1 4 & \frac 1 8\\ 0&\frac 1 2&\frac 2 4& \frac 3 8\\ 0&0&\frac 1 4 & \frac 3 8\\ 0&0&0&\frac 1 8 \end{matrix}\right]\times\left(\begin{matrix}(1-t)^3\\3(1-t)^2t\\3(1-t)t^2\\t^3\end{matrix}\right),t\in[0, 1] \end{aligned}
f(t)=(1−t)3⋅A+3(1−t)2t⋅2A+B+3(1−t)t2⋅4A+2B+C+t3⋅8A+3B+3C+D,t∈[0,1]=(ABCD)×⎣⎢⎢⎡1000212100414241081838381⎦⎥⎥⎤×⎝⎜⎜⎛(1−t)33(1−t)2t3(1−t)t2t3⎠⎟⎟⎞,t∈[0,1]
接下来这一步需要比较复杂的整理,具体的步骤我们就不做了,简单而言,我们要将上面的三个矩阵中的后两个乘起来:
f
(
t
)
=
(
A
B
C
D
)
×
(
(
1
−
t
2
)
3
3
(
1
−
t
2
)
2
t
2
3
(
1
−
t
2
)
(
t
2
)
2
(
t
2
)
3
)
=
f
3
(
t
2
)
,
t
∈
[
0
,
1
]
f(t)=\left(\begin{matrix}A&B&C&D \end{matrix}\right)\times \left(\begin{matrix}(1-\frac t 2)^3\\3(1-\frac t 2)^2 \frac t 2\\3(1- \frac t 2)\left(\frac t 2\right)^2\\(\frac t 2)^3\end{matrix}\right)=f_3(\frac t 2), t\in [0, 1]
f(t)=(ABCD)×⎝⎜⎜⎛(1−2t)33(1−2t)22t3(1−2t)(2t)2(2t)3⎠⎟⎟⎞=f3(2t),t∈[0,1]
这也就说明了,当 t t t 从 0 0 0 取到 1 1 1 时, f ( t ) f(t) f(t) 恰好取遍曲线 f 3 f_3 f3 的前一半。因此以 A E J M AEJM AEJM 为控制多边形的贝塞尔曲线恰好为以 A B C D ABCD ABCD 为控制多边形的贝塞尔曲线的前一半;同理,以 M K G D MKGD MKGD 为控制多边形的贝塞尔曲线恰好为以 A B C D ABCD ABCD 为控制多边形的贝塞尔曲线的后一半。
按照这一原理,我们可以设计一个递归算法来绘制一条贝塞尔曲线:当我们要绘制以 A B C D ABCD ABCD 为控制多边形的贝塞尔曲线时,我们先要计算 B B B 点和 C C C 点到 A D AD AD 的距离,如果 B B B 点和 C C C 点到 A D AD AD 的距离都很近,换言之, A B C D ABCD ABCD 近似共线,我们就不再递归直接将线段 A D AD AD 视为对贝塞尔曲线的近似。如果 B B B 或 C C C 中有一者离线段 A D AD AD 很远,将这个贝塞尔曲线按照上述方法分成 A E J M AEJM AEJM 和 M K G D MKGD MKGD 两部分,并分别递归地进行绘制。

![[附源码]计算机毕业设计学生综合数据分析系统Springboot程序](https://img-blog.csdnimg.cn/8fac5d93f1514737bde372a85756aa66.png)