文章目录
- 一.STL设计思想:容器适配器
- STL--stack的代码设计
- STL--queue的代码设计
- stack和queue的默认容器适配器deque的数据结构解析
- deque的存储结构示意图
- 二.C++仿函数
- 仿函数示例
- 三.STL--priority_queue(优先级队列)
- 1.C++优先级队列的数据结构
- 2.priority_queue的实现框架
- 比较函数(仿函数)的设计
- priority_queue类模板实例化示例
- 3.堆的向上调整接口实现
- 4.堆的向下调整接口实现
- 5.priority_queue类模板
一.STL设计思想:容器适配器
在STL的实现中,经常会复用已经完成实现的容器去实现另外一种容器(代码复用思想的具体体现),此时,前者(已经完成实现的容器)就称为后者(待实现的容器)的容器适配器,容器适配器的类型在代码设计中作为待实现容器的类模板参数.
比如,STL的stack和queue就是利用容器适配器思想来实现的
STL–stack的代码设计
template<class T, class container = deque<T>>
class stack
{
public:
stack()
{}
void push(const T& x)
{
_c.push_back(x);
}
void pop()
{
_c.pop_back();
}
T& top()
{
return _c.back();
}
const T& top()const
{
return _c.back();
}
size_t size()const
{
return _c.size();
}
bool empty()const
{
return _c.empty();
}
private:
container _c;
};
STL–queue的代码设计
template<class T, class container = deque<T>>
class queue
{
public:
queue()
{}
void push(const T& x)
{
_c.push_back(x);
}
void pop()
{
_c.pop_front();
}
T& back()
{
return _c.back();
}
const T& back()const
{
return _c.back();
}
T& front()
{
return _c.front();
}
const T& front()const
{
return _c.front();
}
size_t size()const
{
return _c.size();
}
bool empty()const
{
return _c.empty();
}
private:
container _c;
};
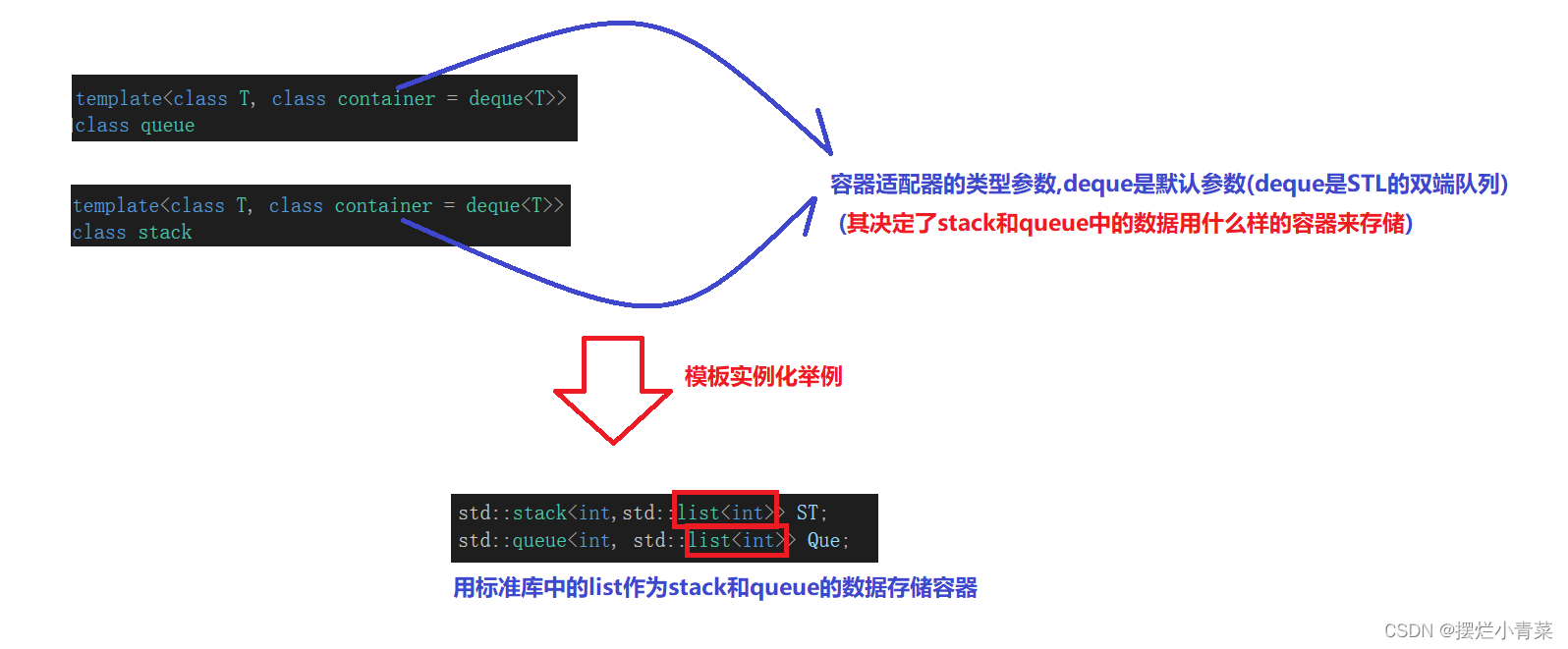
- 根据stack和queue的实现框架可知,它们容器适配器必须支持数据的尾插,尾删, 头插,头删等等操作,用类型不合适的容器适配器去实例化stack和queue无法通过编译
stack和queue的默认容器适配器deque的数据结构解析
deque是STL标准库中的双端队列,其存储结构是用指针数组管理的一系列数组集合,它同时支持时间复杂度为O(1)的数据头插头删,尾插尾删操作
deque的存储结构示意图
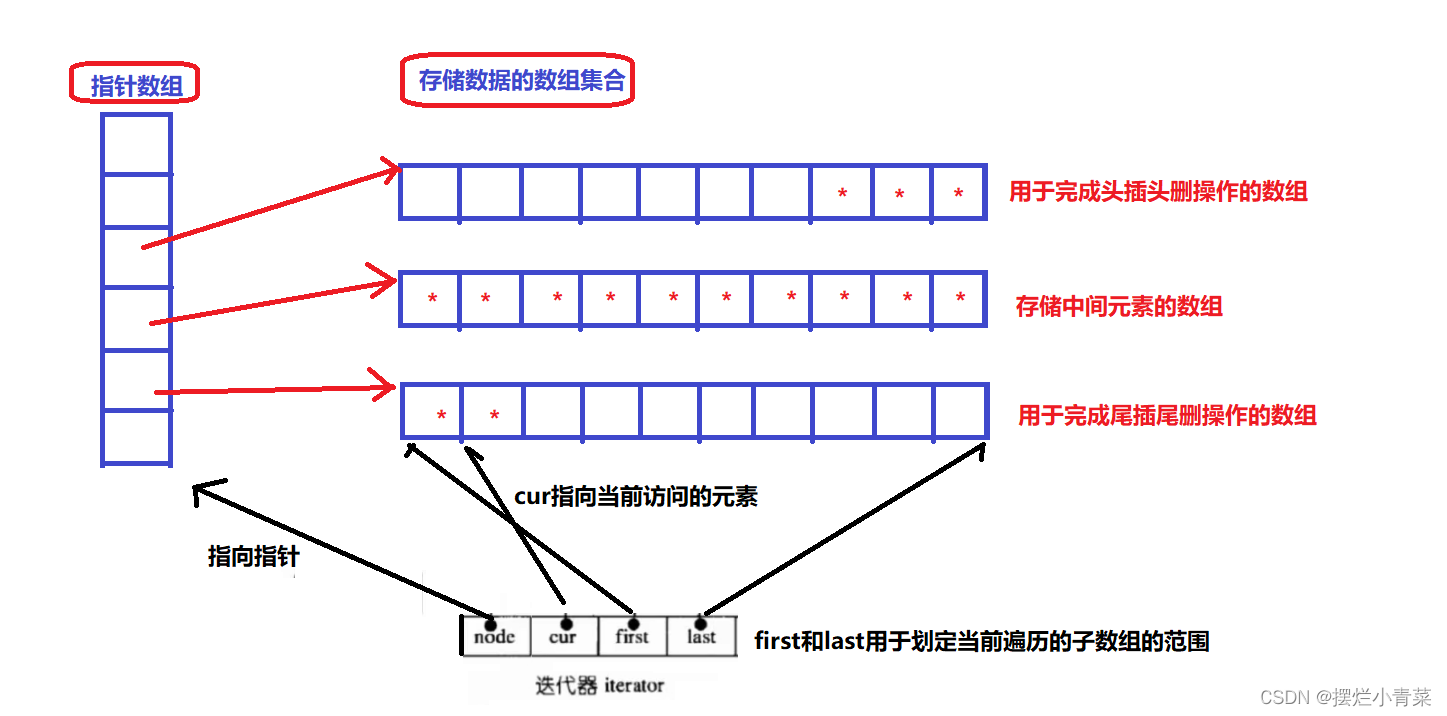
- 分析deque的存储结构易知:deque的元素随机访问(下标访问)操作运算量较大,因此效率不高,而且在deque容器的中间位置插入或删除元素性能消耗非常巨大,而且deque的迭代器实现非常复杂
- 因此有以下结论:
- deque非常适合进行数据的头尾插入和删除操作,因此可以作为stack和queue的默认适配容器
- 当使用场景涉及在容器的中间位置插入或删除元素时,首选list,使用deque效率会非常低
- 当算法需要大量的元素随机访问操作时(比如快排),优先使用vector
二.C++仿函数
C++中的仿函数实质上是将()运算符重载封装在类中,使被封装起来的函数其可以依托于类对象作为"函数形参"传入其他函数中进行调用,C++设计仿函数的目的是为了取代C语言中的函数指针,有效地提高了代码的封装性
仿函数示例
- 基于仿函数设计出来的两个数据比较函数
template<class DataType>
class less
{
public:
bool operator()(const DataType& data1, const DataType& data2)
{
return data1 < data2;
}
};
template<class DataType>
class greater
{
public:
bool operator()(const DataType& data1, const DataType& data2)
{
return data1 > data2;
}
};
- 调用示例:

三.STL–priority_queue(优先级队列)
1.C++优先级队列的数据结构
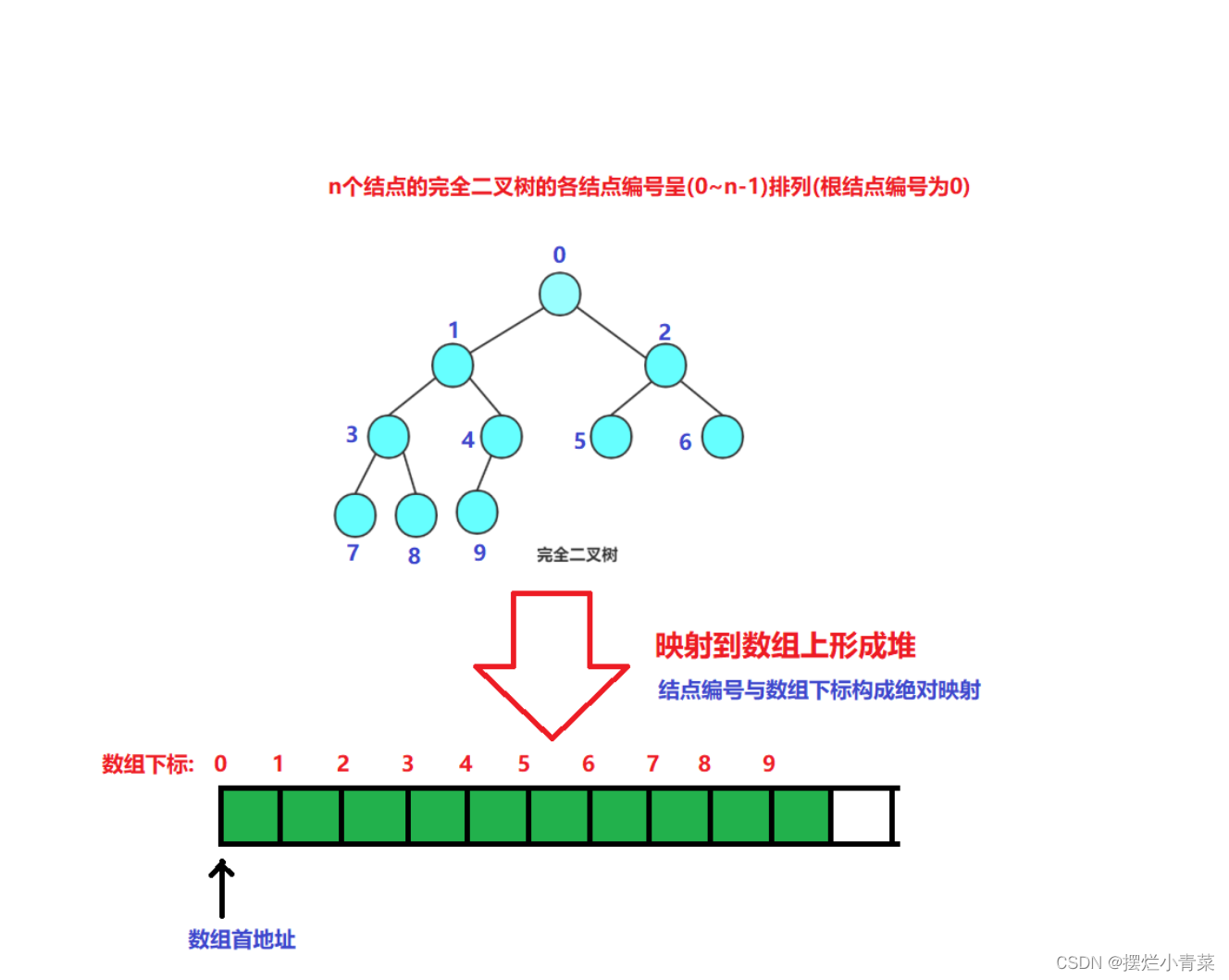
- priority_queue的逻辑结构是一颗完全二叉树,其存储结构一般采用vector作为其默认容器适配器(容器适配器类型可由用户来决定,然而由于堆的上下调整算法涉及频繁的元素随机访问操作,因此大多数情况下vector都是priority_queue的最佳容器适配器)
2.priority_queue的实现框架
template<class DataType, class Container = std::vector<DataType>, class Compare = less<DataType>>
class priority_queue
{
public:
// 创造空的优先级队列
priority_queue() {};
//用迭代器区间建堆,采用元素向下调整法建堆
template<class Iterator>
priority_queue(Iterator first, Iterator last);
//堆插入接口
void push(const DataType& data);
//堆顶元素出队接口
void pop();
//返回队列元素个数的接口
size_t size()const;
//队列判空接口
bool empty()const;
// 堆顶元素不允许修改,因为:堆顶元素修改可以会破坏堆的特性
const DataType& top()const;
private:
//元素向上调整接口
void AdjustUP(int child);
//元素向下调整接口
void AdjustDown(int parent);
}
private:
//储存堆的物理容器
Container _array;
};
- priority_queue类模板首部分析:
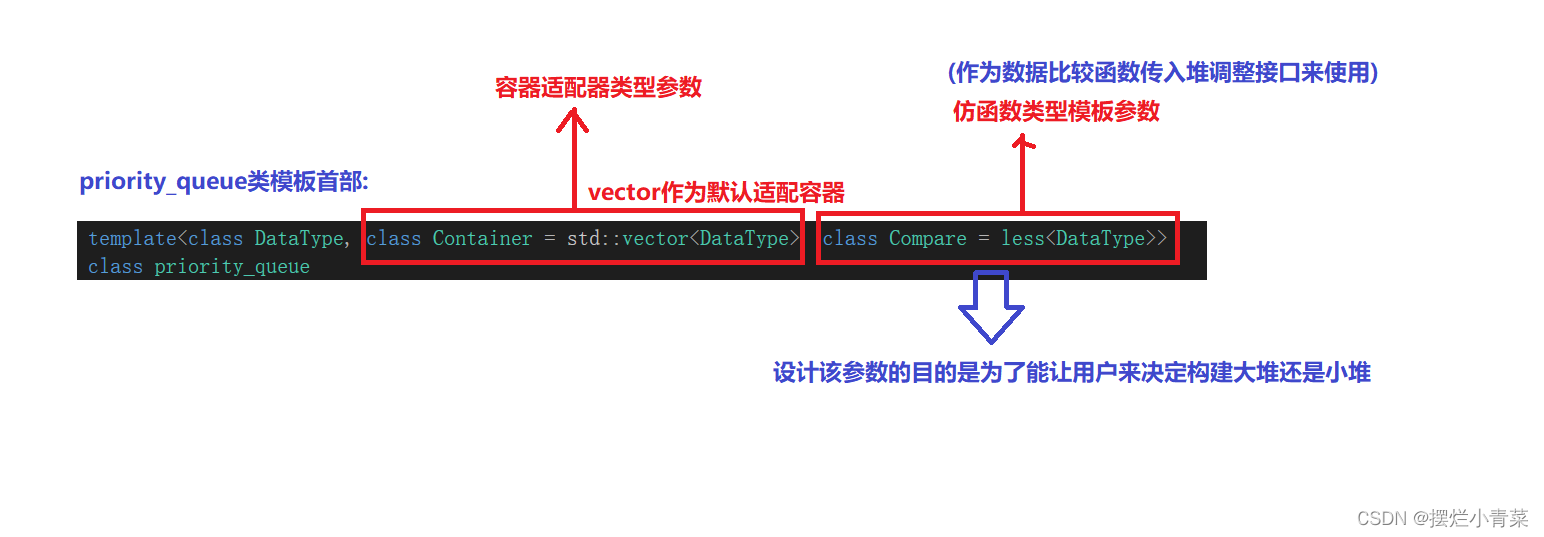
比较函数(仿函数)的设计
//用仿函数来实现比较器,用于控制堆的类型
//用于建大堆的比较函数
template<class DataType>
class less
{
public:
bool operator()(const DataType& data1, const DataType& data2) const
{
return data1 < data2;
}
};
//用于建小堆的比较函数
template<class DataType>
class greater
{
public:
bool operator()(const DataType& data1, const DataType& data2) const
{
return data1 > data2;
}
};
- 用
less<DataType>来实例化priority_queue的Compare模板参数则建立大根堆 - 用
greater<DataType>来实例化priority_queue的Compare模板参数则建立小根堆
priority_queue类模板实例化示例
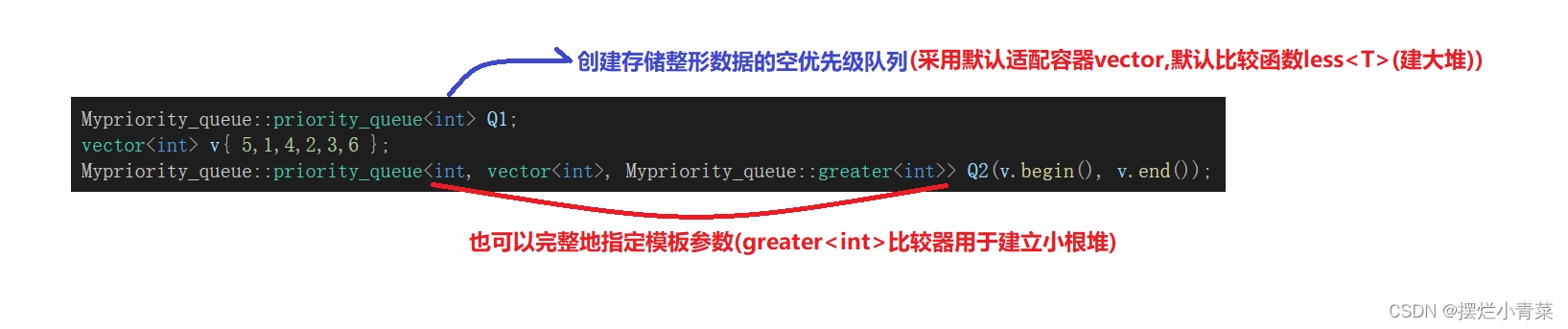
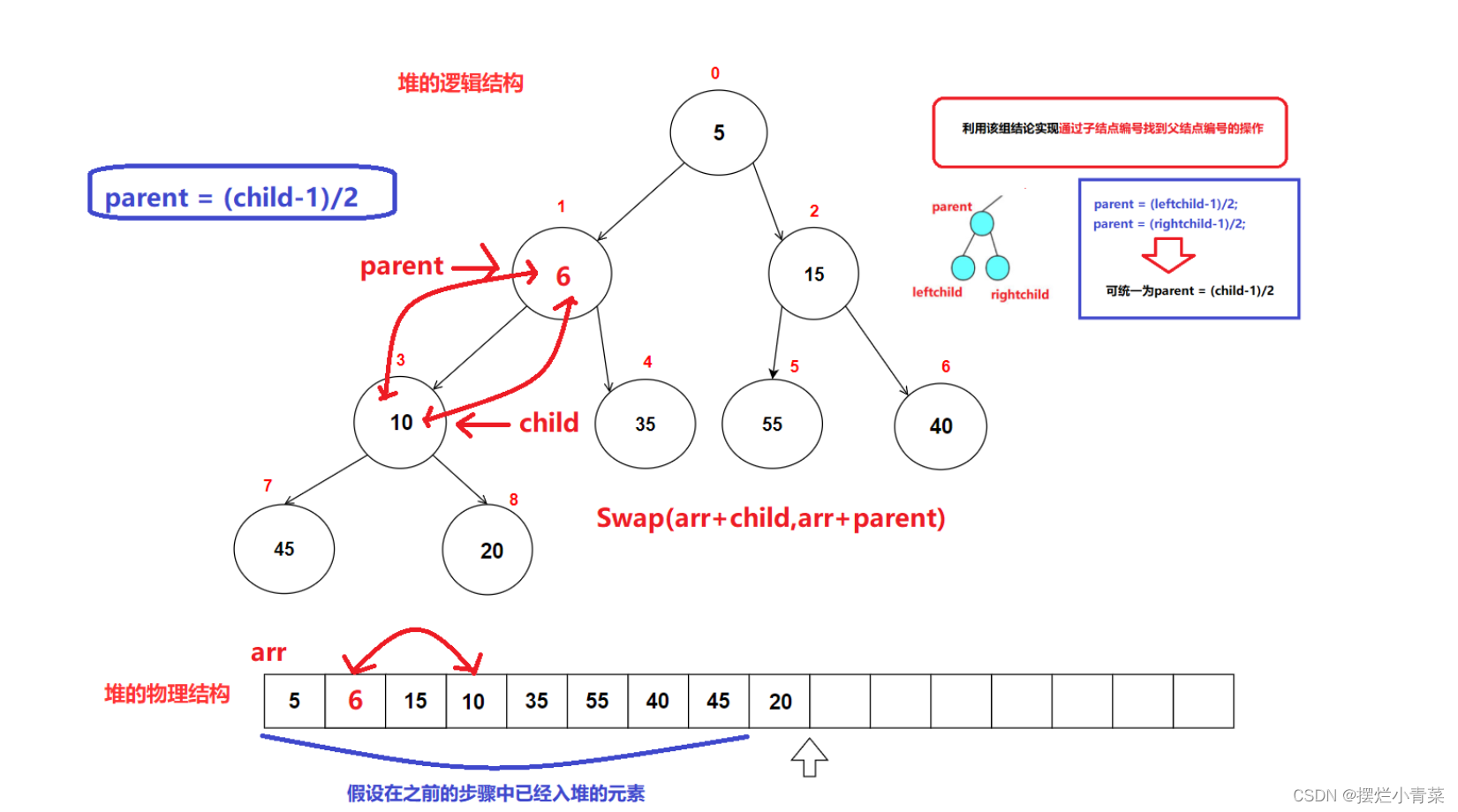
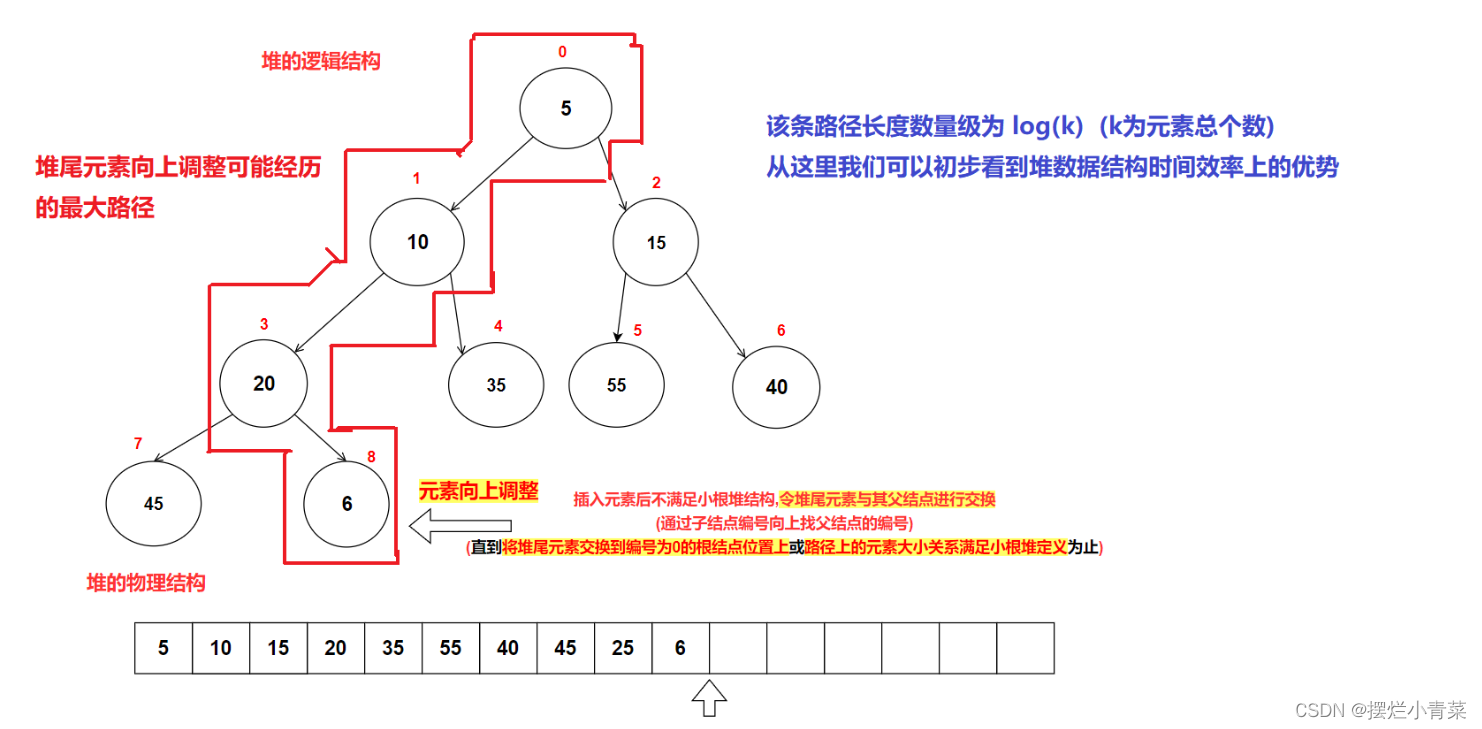
3.堆的向上调整接口实现
- 图解以小根堆为例:
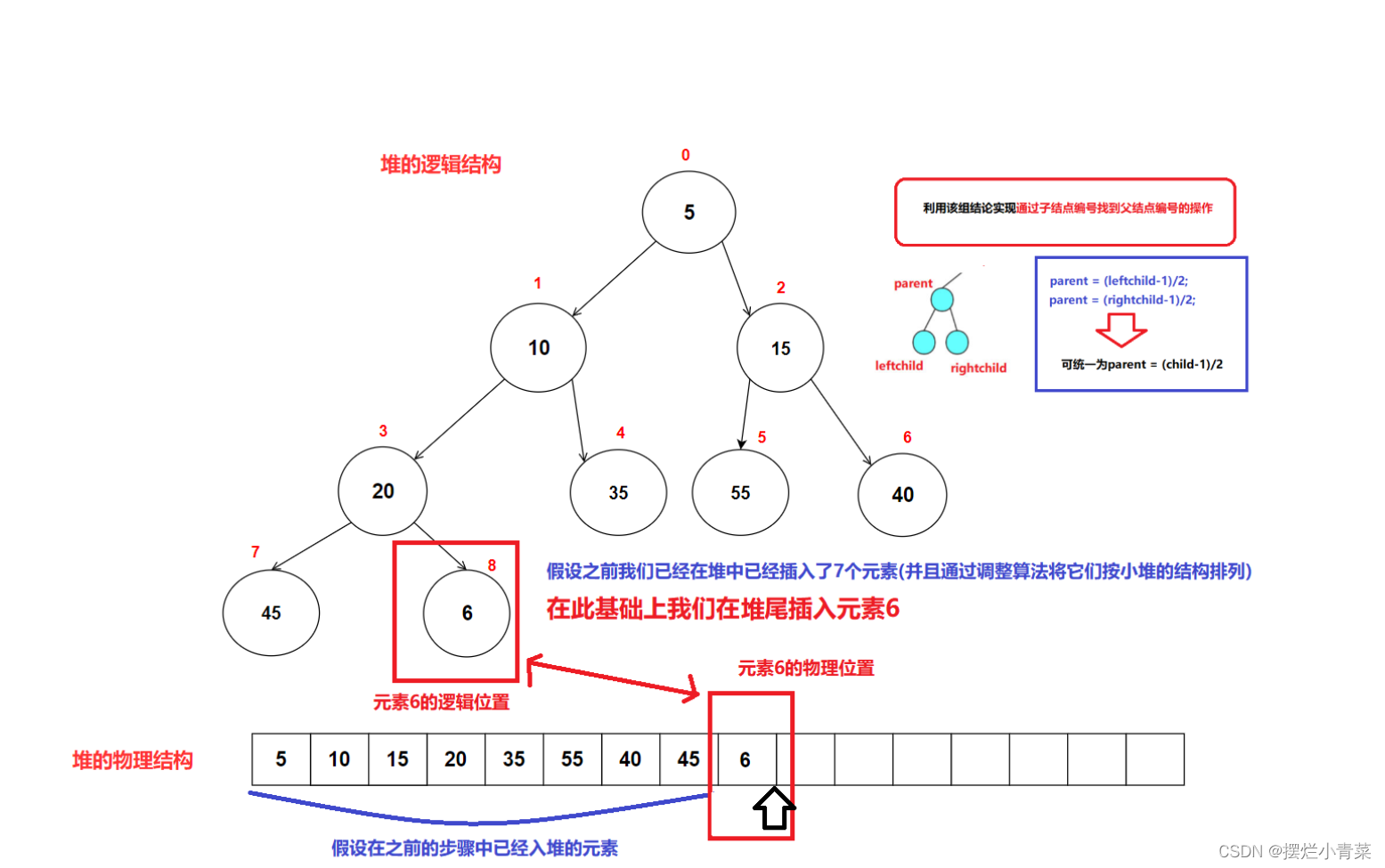
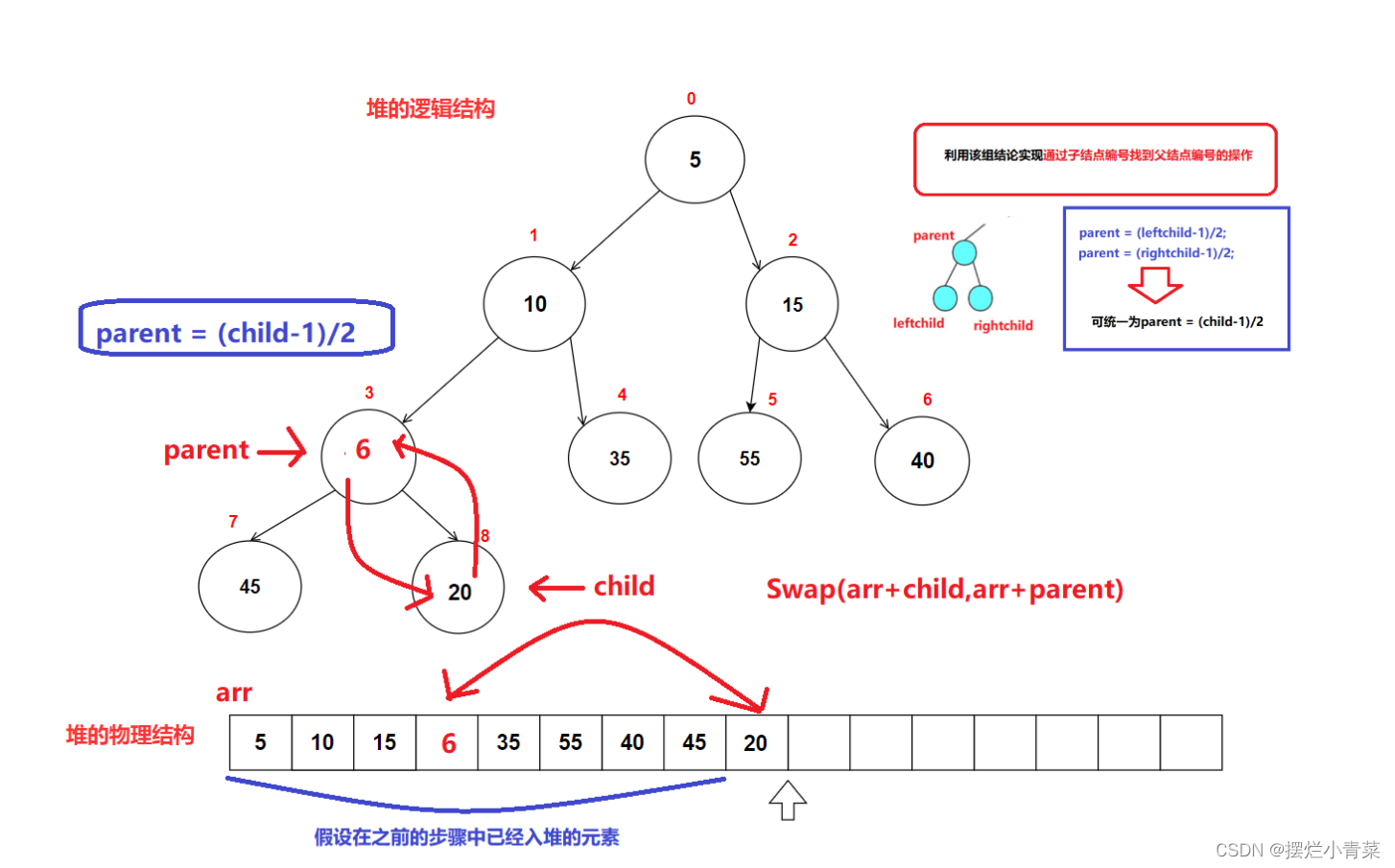
//元素向上调整接口
void AdjustUP(int child)
{
//创建数据比较函数(仿函数类)
Compare comparator;
int parent = (child - 1) / 2;
while (child > 0)
{
if (comparator(_array[parent] , _array[child]))
{
std::swap(_array[child], _array[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
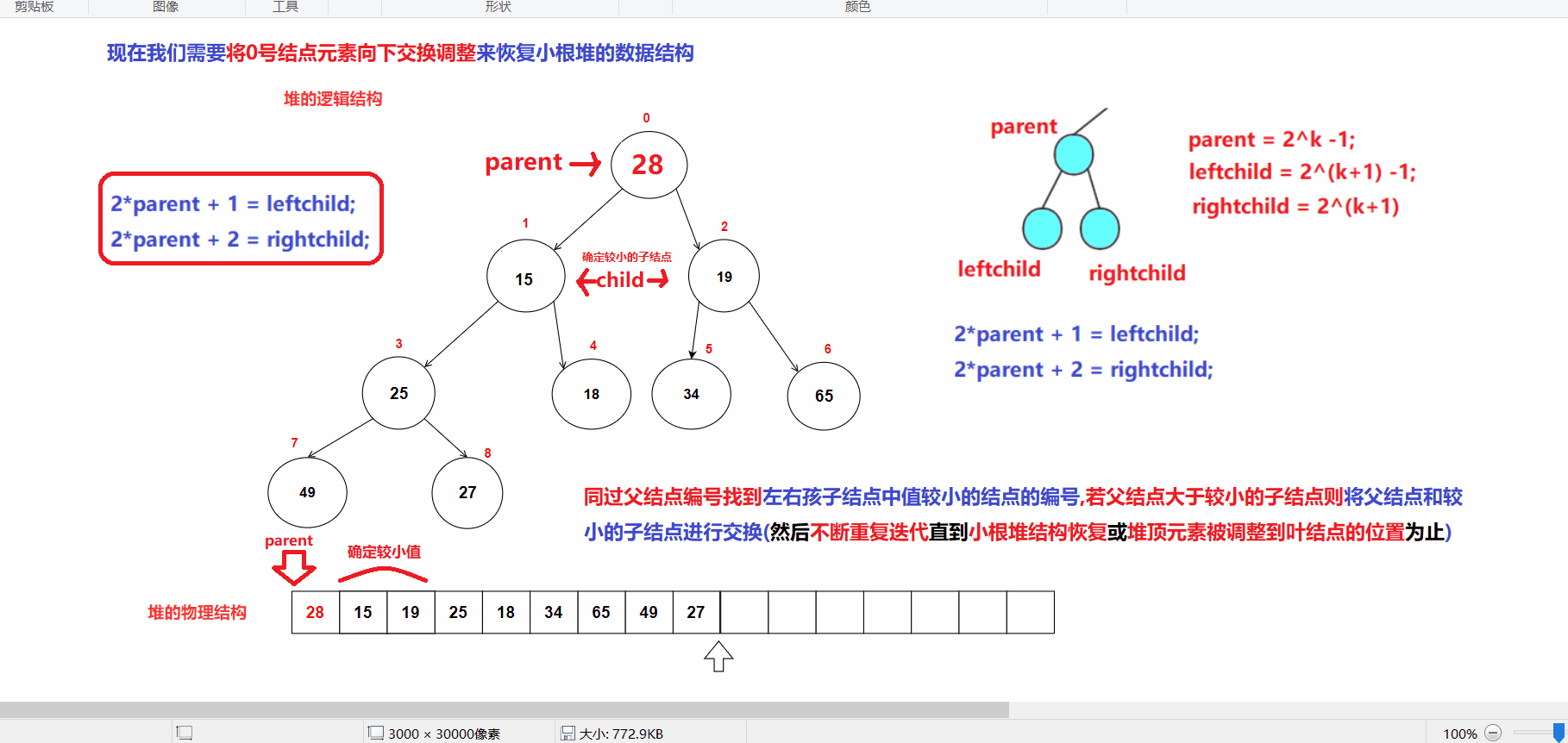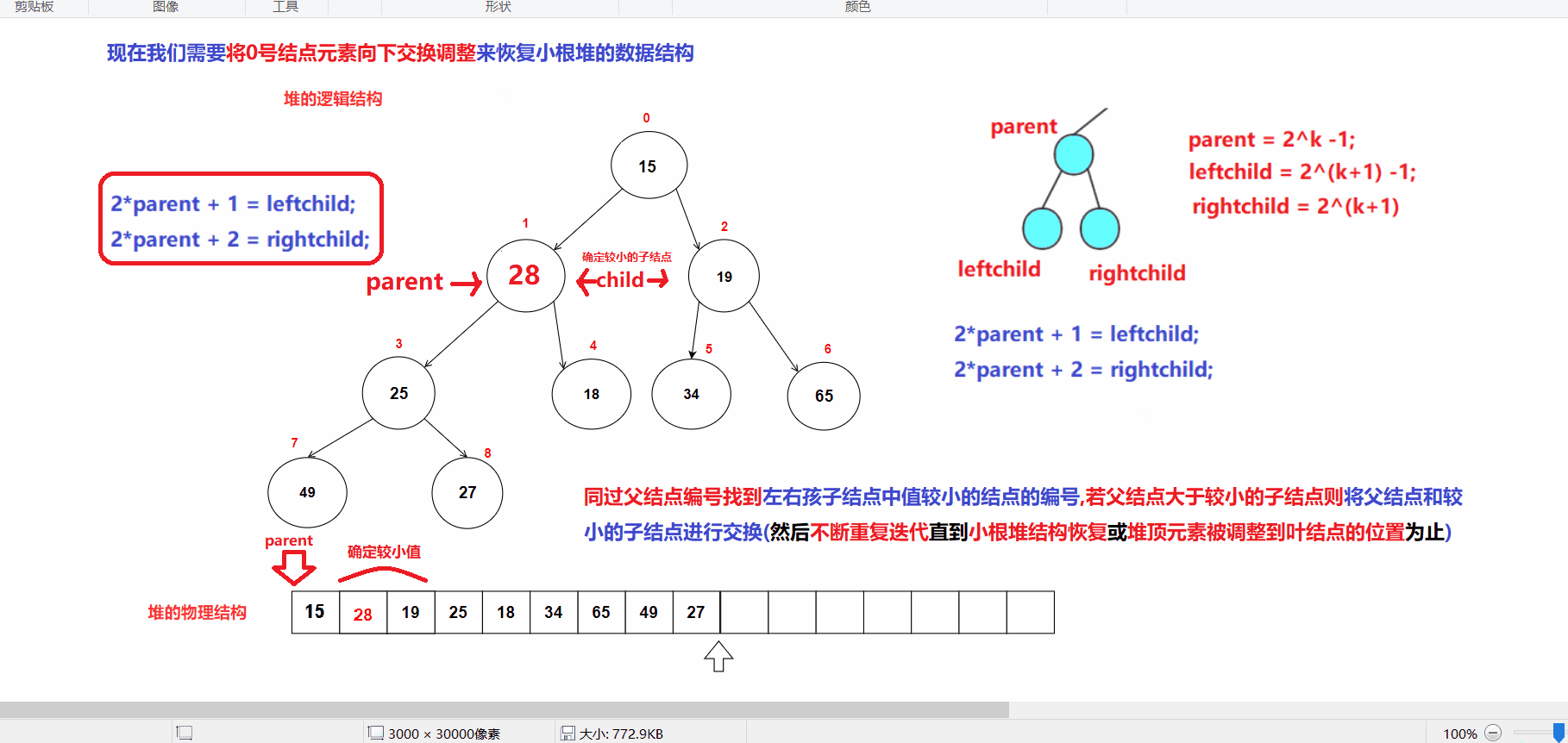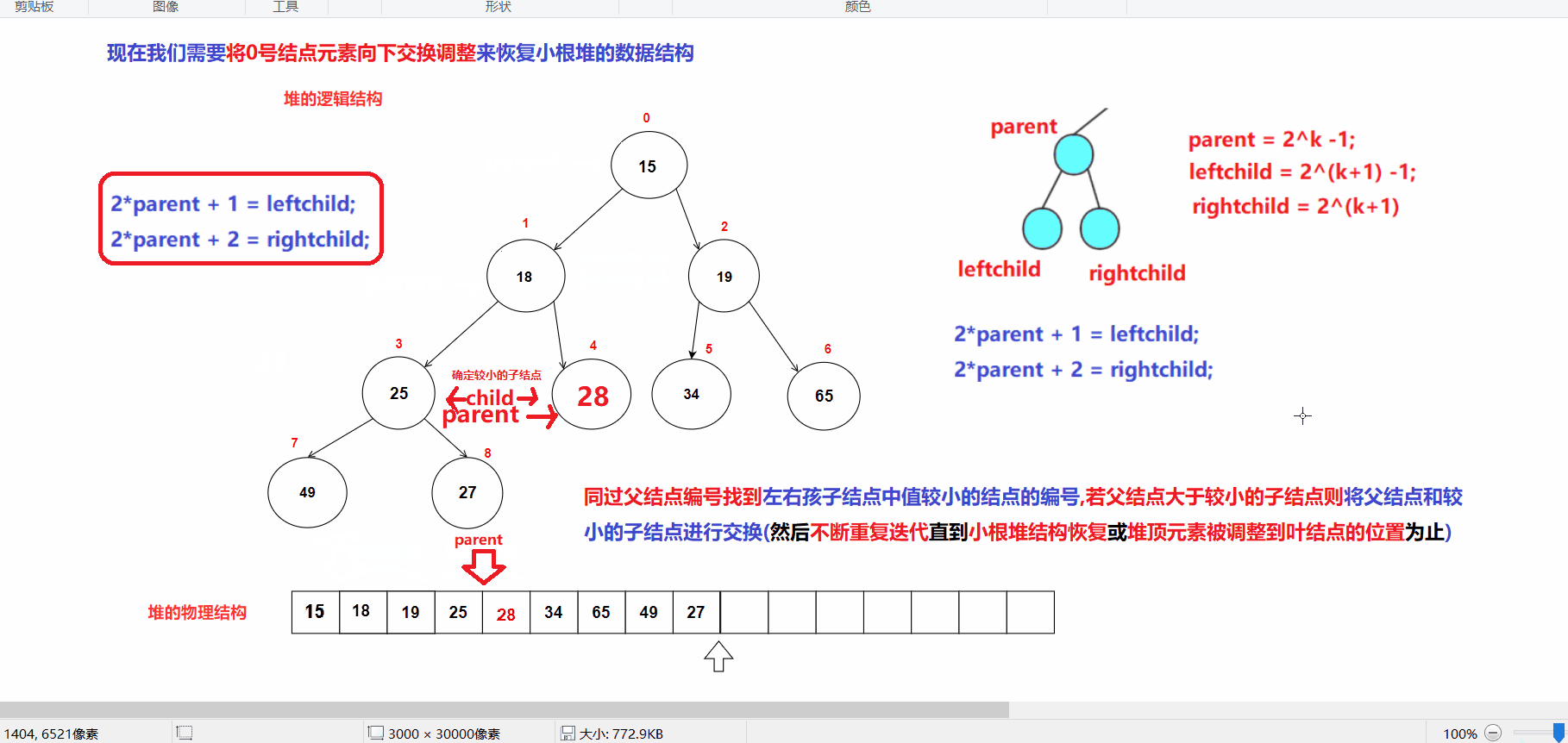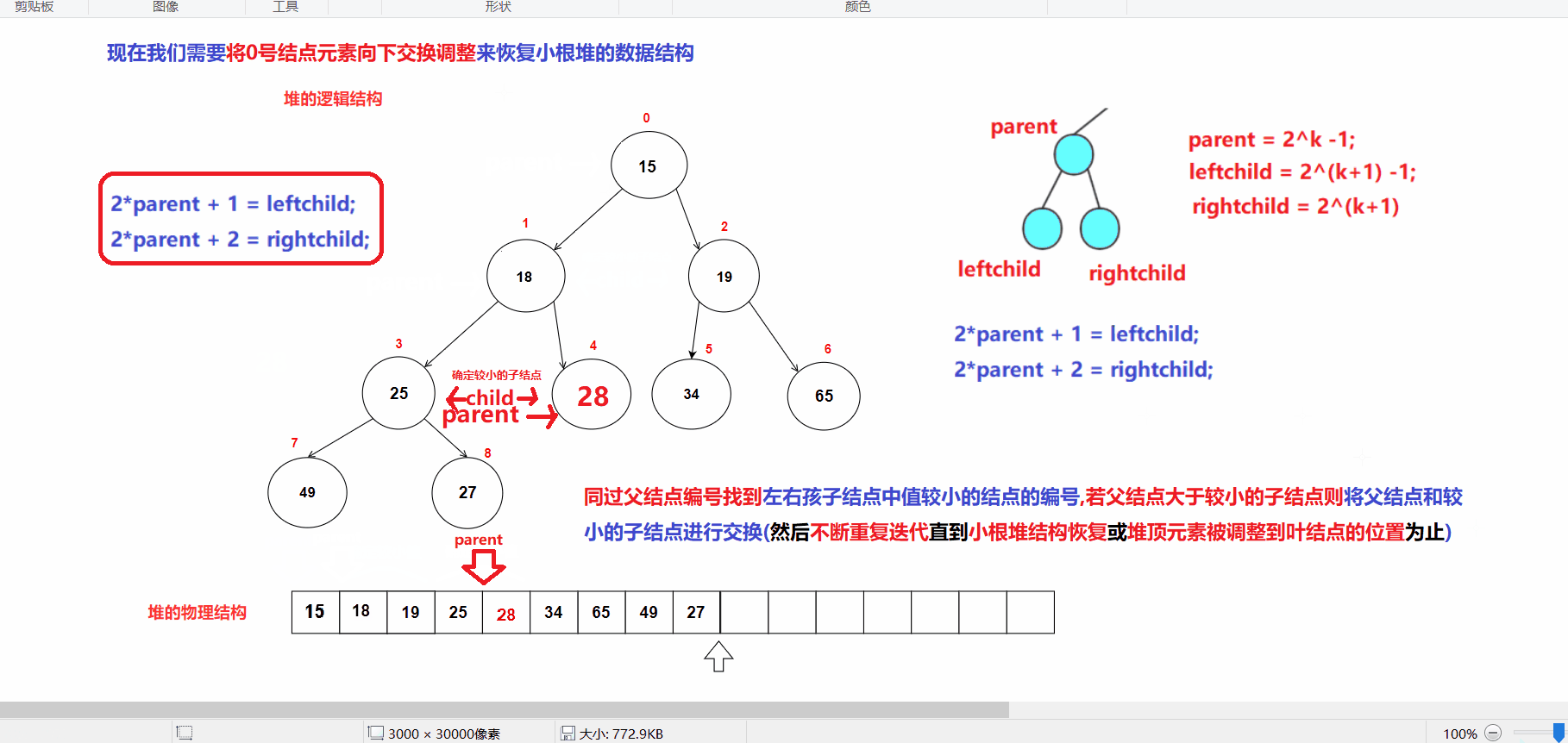
4.堆的向下调整接口实现
- 堆的向下调整动图:
//元素向下调整接口
void AdjustDown(int parent)
{
//创建数据比较函数(仿函数类)
Compare comparator;
//先取左孩子
int child = 2 * parent + 1;
while (child < size())
{
//取出左右孩子的较大值(或较小值)
if (child + 1 < size() && comparator(_array[child] , _array[child + 1]))
{
child++;
}
if (comparator(_array[parent] , _array[child]))
{
std::swap(_array[parent], _array[child]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
5.priority_queue类模板
namespace Mypriority_queue
{
//用仿函数来实现比较器,用于控制堆的类型
//用于建大堆的比较函数
template<class DataType>
class less
{
public:
bool operator()(const DataType& data1, const DataType& data2) const
{
return data1 < data2;
}
};
//用于建小堆的比较函数
template<class DataType>
class greater
{
public:
bool operator()(const DataType& data1, const DataType& data2) const
{
return data1 > data2;
}
};
template<class DataType, class Container = std::vector<DataType>, class Compare = less<DataType>>
class priority_queue
{
public:
// 创造空的优先级队列
priority_queue() {};
//用迭代器区间建堆,采用元素向下调整法建堆
template<class Iterator>
priority_queue(Iterator first, Iterator last)
{
//将元素都尾插到数组中
for (auto it = first; it != last; ++it)
{
_array.push_back(*it);
}
//采用向下调整建堆,建堆时间复杂度为O(N);
for (int tail = (size() - 1 - 1) / 2; tail >= 0; --tail)
{
AdjustDown(tail);
}
}
//堆插入接口
void push(const DataType& data)
{
//先将元素尾插到容器中,再执行元素向上调整
_array.push_back(data);
AdjustUP(size() - 1);
}
//堆顶元素出队接口
void pop()
{
assert(!empty());
//先将堆顶元素交换到堆尾,然后将堆尾元素移除,最后将堆顶元素向下调整恢复堆的结构
std::swap(_array.front(), _array.back());
_array.pop_back();
AdjustDown(0);
}
//返回队列元素个数的接口
size_t size()const
{
return _array.size();
}
//队列判空接口
bool empty()const
{
return 0 == size();
}
// 堆顶元素不允许修改,因为:堆顶元素修改可以会破坏堆的特性
const DataType& top()const
{
assert(!empty());
return _array.front();
}
private:
//元素向上调整接口
void AdjustUP(int child)
{
Compare comparator;
int parent = (child - 1) / 2;
while (child > 0)
{
if (comparator(_array[parent] , _array[child]))
{
std::swap(_array[child], _array[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
//元素向下调整接口
void AdjustDown(int parent)
{
Compare comparator;
//先取左孩子
int child = 2 * parent + 1;
while (child < size())
{
//取出左右孩子的较大值
if (child + 1 < size() && comparator(_array[child] , _array[child + 1]))
{
child++;
}
if (comparator(_array[parent] , _array[child]))
{
std::swap(_array[parent], _array[child]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
private:
//储存堆的物理容器
Container _array;
};
}
- 值得注意的是利用迭代器区间建堆的构造函数采用的建堆方式是向下调整建堆法,其时间复杂度为O(N),在众多算法实现中这是一个非常常用的建堆接口,关于堆的数据结构理论分析参见:堆的实现与建堆时间复杂度分析