介绍

 计算机视觉（Computer Vision，CV）是一门使用计算机模拟生物视觉的学科，目的是使用计算机代替人眼实现对目标的识别、分类、跟踪和场景理解。计算机视觉是人工智能的重要分支，也是人工智能最为活跃的研究方向之一。
 人类的感知信息绝大部分是通过视觉获取的。周围物体在可见光的照射下，在人眼的视网膜上形成图像，有感光细胞转化成神经脉冲信号，经神经纤维传入大脑皮层进行处理和理解。视觉，不仅指对光信号的感受，还包括了对视觉信息的获取、传输、处理、存储和理解的全过程。 根据下图的视觉通路，我们可以看到眼、外侧膝状核与视皮层构成对视觉信息处理的三个层次结构。不同区域的神经细胞具有不同的功能。视觉通路上各层次的神经细胞从简单到复杂，它们所处理的信息分别对应于视网膜上的一个局部区域。层次越深入，该区域就越大，这就是感受野（Receptive Field）和感受野等级假设。

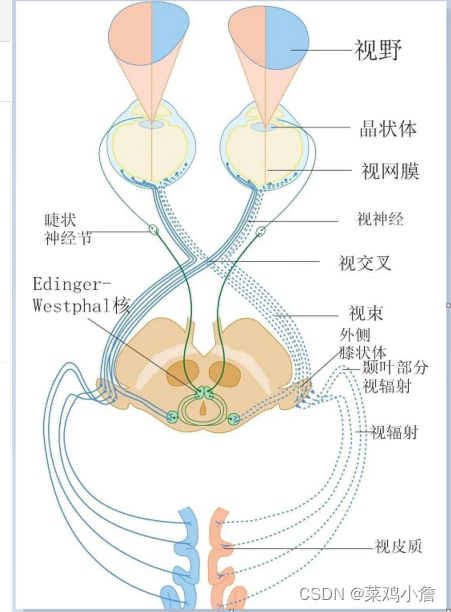
 视觉传导通路由三级神经元组成。第一级神经元未视网膜的双极细胞，第二级神经元是节细胞，第三级神经元的胞体在外侧膝状核内。其中第一级神经元中，视网膜上的神经节细胞（Gauglion Cell，GC）将感光细胞上接受的光信号转换成电信号，再由他的轴突传出。但每一个GC只能接收视网膜上一个局部区域信号，该区域是GC的感受野，其对光信号的转换作用如下：
   （1）对空间亮度变化敏感的感受野，形状可用两个同心圆标识。其同心圆形状的感受野按其对光信号的转换作用可分为中心兴奋区、周边抑制区组成的on-中心型以及中心抑制、周边兴奋区组成的off-中心型。当视网膜上的光信号为一边亮一边暗的具有一定对比度的信号时，只有当亮暗边缘线过同心圆中心时，GC的输出与感受野收到均匀光照时一样为平均输出。而当边缘线位于同心圆其他位置时，输出分别高于或低于该平均输出。如将输出看作实际输出减去平均输出，则由GC的输出与感受野位置可以检测亮暗边缘线，这也是边缘抽取的生物学基础。
   （2）除了GC细胞（x型细胞）外，还存在一种y型细胞，它相应对亮度空间变化不敏感，而对时间变化敏感。即当感受野圆形区域内的亮度随时间变化时，GC输出会增大或减少，y性细胞可以划分为on型或off型。这种对局部亮度随时间变化敏感的性质，是对物体运动分析的基础。


 上述的x/y型细胞是视觉信息处理的中视觉传导通路第一级神经元。对于更高层次，包括外侧膝状核细胞与初级视皮层，也是存在相似的性质。感受野的等级假设与局部性质主要支持视觉信息处理的自下而上的额分层次串行处理性质。但视觉系统的任务不是单一的，它要识别物体的形状和颜色，要得到三维物体的深度信息，要检测物体的方位与运动参数。另外，物体的空间与时间频率性质也有很大差异。神经生物学的研究表明，视觉通路的各层次上存在着基本互相独立的并行通道，分别完成不同的视觉任务，具体通道如下：
   （1）x、y型通道 —— 由于x、y型感受野的不同，x型通道传递高空间分辨率的、时间上变化的信息与颜色信息；y型通道传递低空间分辨率的、高时间变化率的信息。
   （2）空间与时间频率通道 —— x、y型细胞分别对具有空间频率或时间频率的信息敏感。心理物理学实验证明，外侧膝状核上的某一个神经细胞并不对所有频率的信息敏感，而是对某一频率的信息呈现较强的反应，在视觉皮层也发现了相似的证据。这些证据可以表明视觉通路中存在处理不同频率信号的独立通道。
   （3）颜色信息通道 —— 视网膜存在不同的光感受细胞，即锥状细胞与杆状细胞，其中杆状细胞对颜色不敏感，而锥状细胞又分为对不同光谱（红、绿、蓝）敏感的三种细胞，对外侧膝状核与视觉皮层17区的分析也表明，他们都存在专门的区域从事颜色信息的处理与识别。
   （4）左右眼信息通道与立体视觉 —— 从视觉通路的图片中，可以看出眼睛、外侧膝状核与视皮层都存在左右侧。分析表明，左右两侧的神经细胞分别处理来自左右半侧的信息。也就是说，每一个眼睛的左右侧视野信息是交叉投射到左右侧外侧膝状核与视皮层。视皮层处理来自两眼的信息，其得到两眼视察信息，即立体视觉的基础。只有比较两眼的信息，才能使我们有深度感。
   （5）空间方位信息通道 —— 早期对视觉通路信息处理的研究认为，视皮层细胞对空间几何元素的方位敏感。阮迪云等对外侧膝状核细胞的研究表明，这种方位敏感也存在于外侧膝状核细胞。
   （1）视皮层对形状、颜色、运动与深度信息的并行处理 —— 对视皮层17区至更高层次的研究表明。对物体的形状、颜色、运动与深度等不同视觉信息的处理已明显分离开。


 边缘检测使图像处理和计算机视觉中的最基本问题，边缘检测的目的是标识数字图像中亮度变化明显的点。图像属性中的显著变化通常反映了属性的重要事件和变化。这些包括深度上的不连续、表面方向的不连续、物质属性变化和场景照明变化。边缘检测是图像处理和计算机视觉中，尤其是特征提取中的一个研究领域。

边缘检测与微分运算

 对于二维图像而言，边缘一般发生在一阶微分的最大值处或者二阶微分的过零点处。设二维图像信号为f(x, y)，这里（x, y）表示像素点的位置。则其一阶导数为：

 而对于二阶导数，一般采用激光一种各向同性的二阶微分算子，即拉普拉斯算子：

 由于实际信号常存在噪声，如果只是按照一阶和二阶微分的最大值和过零点检测边缘点，会由于噪声的存在出现很多的假边缘点。因此，在实际运用过程中需要优先去除噪声。噪声信号通常为高频信号，可以通过对其进行平滑滤波，去除噪声。平滑滤波器表示为h(x, y)，滤波过程实际是在空域上的一个卷积运算。具体如下

 将一阶和二阶微分操作和滤波去噪的过程结合，并利用卷积操作的性质，可以分别得到下述表达式：

 则可以线计算出平滑滤波器的一阶微分和二阶微分，而后和图像本身做一次卷积操作即可。平滑滤波器一般选择为高斯滤波器，其二维表示及其一阶和二阶微分如下所示：

离散信号的差分滤波

 实际存储与计算机内的信号为离散信号，离散卷积运算可以看作算子运算，即将下述窗口算子沿信号移动，在每一点滤波后的值等于窗口内信号的加权平均。常用的表示微分操作的算子包括Robert算子，Prewitt算子，Sobel算子和拉普拉斯算子。

Robert算子

 图示算子分别为两个45°方向的一阶差分滤波器，成为Robert算子。用它们对图像滤波，可以计算沿两个45°方向的一阶差分。

Prewitt算子

 左边为y方向一阶差分与x方向的平滑滤波，右边为x方向一阶差分和y方向的平滑滤波。

Sobel算子

 左边为y方向一阶差分与x方向的平滑滤波，右边为x方向一阶差分和y方向的平滑滤波。与Prewitt算子在平滑部分的加权值存在差异。

拉普拉斯算子

 二阶差分滤波器，也称为拉普拉斯算子，该算子不包含平滑滤波器。

 上述滤波器窗口一般都是3*3滤波器，也可以用σ较大的高斯函数的差分或者其他平滑函数差分设计较大窗口的差分算子，以有效抑制噪声。但窗口越大，计算复杂性越高。