1. 摘要
在我们所熟知经典SLAM系统,以ORB-SLAM为代表的通过特征点法在相机位姿估计方面有很好的表现,但在一些人为构造的弱纹理环境下,由于缺少可靠的特征点的缘故,导致表现性能下降。
针对此种问题,作者通过根据周围环境的几何特征来提升结构化环境下的SLAM追踪和建图准确性。除特征点以外,我们还可以利用结构化环境提供的大量线和面的特征来进行SLAM系统的追踪与建图。
在SLAM的追踪模块中,作者对位置和姿态进行了解耦合的优化处理,同时利用曼哈顿假设对位姿进行优化。对于建图部分,从稀疏到稠密不同等级的地图可以以较低的计算量进行重建。作者使用实例化网格的策略,根据平面网格实例的独立性来建立稠密地图。
2. 引言
解决长期漂移问题一般有两种方法:一是回环检测,二是对环境结构进行假设,例如曼哈顿假设。
下图就是典型的曼哈顿结构中的建图流程。环境中包含线和面,它们朝向笛卡尔坐标系的三个正交方向中的一个。在室内场景中,墙、地面、屋顶一般在任何一个房间中都是相互正交或者平等的,非常符合曼哈顿假设。

本文主要贡献
- 基于曼哈顿假设原理,对位姿进行解耦。通过联合平面上的点、线特征以及附加的基于曼哈顿约束的位姿优化过程来提升位姿估计的准确性。
- 提出平面实例化网格方法,将稀疏点云中生成一个轻量化环境表征。
- 提出在结构环境下具有高精度的实时RGB-D SLAM系统。
3. 场景结构分析

作者结合点、线、面这三者的特征来对提高系统在结构化弱纹理场景下的稳定性,点特征采用ORB特征点,特征点的提取通过LSD方法[A Fast Line Segment Detector with a False Detection Control],由于RGB-D的缘故,我们可以直接得到稠密点云,通过 Efficient Organized Point Cloud Segmentation with Connected Components 这篇文章的思想来根据有序点云进行平面分割,平面方程用进行表示。
在点线提取环节,由于RGB-D相机得到的深度图在物体边界处会出现深度不连续的先天性弱势,当我们将特征根据深度值和相机内参进行投影至相机坐标系下时,势必会存在由于深度错误导致投影的不准确情况,为克服这种情况对系统的影响,作者采用啦一个小trick:对3D线进行滤波,即通过RANSAC的方法对线段上的外点进行剔除。
平面的法向量提取这块,作者采用法向量平滑的方式进行处理,即我取一个10×10大小的patch法向量的平均值来对当前法向量进行平滑。而后将我们提取的平面采用Point-Plane SLAM Using Supposed Planes for Indoor Environments 所介绍的数据关联的方法与我们已有平面进行匹配。大致思想就是说我们先对比它们之间的法向量角度的差异,如果小于一定阈值10度,我们可以再将它们的点到面的距离进行对比,如果小于0.1m的话,我们将其插入已观测地图中,同时在地图中加入平面平行和垂直关系为后续的追踪线程提供约束。
3.1. 位姿解耦与优化
在追踪线程中包含相机的旋转、平移的估计以及最后的位姿优化过程。位姿的接耦这部分作者推荐三篇论文供大家学习。
- Divide and Conquer: Efficient ensity-based Tracking of 3D Sensors in Manhattan Worlds
- Globally Optimal Manhattan Frame Estimation in Real-time
- Visual Odometry with Drift-free Rotation Estimation Using Indoor Scene Regularities
后续我会针对这三篇论文进行整理,分享一下我们如何基于曼哈顿大世界的位姿解耦问题,在这里大家只要清楚作者通过在曼哈顿坐标系下求得了我们当前帧与曼哈顿坐标系的旋转矩阵
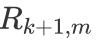
与,基于此我们就可以求得当前帧到世界坐标系下的旋转矩阵:
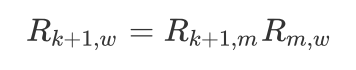
通过这种方式我可以先单独将旋转矩阵分解出来,这样的做法区别于之前根据我们典型的根据相邻帧的对极几何约束所求的本质矩阵或基础矩阵不同,每一帧是在我们的曼哈顿坐标下对旋转矩阵进行求解,这的好处是我们可以杜绝根据由于相邻帧的位姿估计所导致的误差的累计,当然我们通过在曼哈顿世界坐标系下求解的旋转矩阵也仍然存在误差,只不过没有累积误差这一说。
平移向量的估计我们通过构建残差方程,通过最小二乘来实现对平移向量的求解,作者根据点、线、面的约束构建了三个子残差方程,根据特征点的重投影误差所构建的残差方程为:

对于线特征,作者在文章中介绍过于简短,有必要参考论文Accurate and Linear Time Pose Estimation from Points and Lines 在此进行简短的介绍,对线特征的残差构之前,我们使用线特征的归一化法向量来对我们的线特征进行表征。
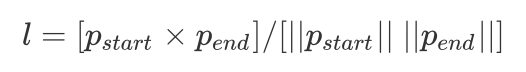
将线特征的端点P、Q投影至齐次坐标系下与观测量点乘得其残差
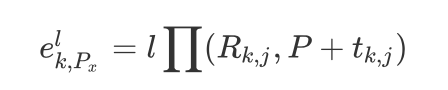
关于线段的残差方程为:

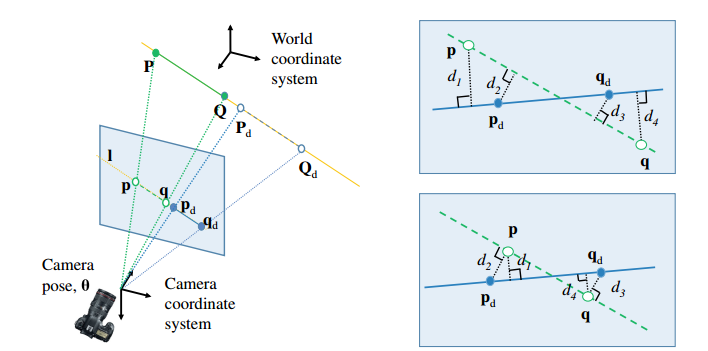
面特征的残差方程为:

我们假设我们的观测量服从高斯分布,那最终的非线性最小二乘可以写为:

3.2. 位姿优化
在进行位姿求解过程中,我们均在理想的曼哈顿假设进行位姿的接偶与估计。在实际环境中难免会出现不严格遵循曼哈顿假设的情况是我们的位姿估计存在偏差,所以在获取到初始化位姿后我们需要通过优化模型对其偏差进行补偿。将根据关键帧建立起局部地图投影到当前帧进行匹配搜索,另为作者加入平行和垂直的关系对平面进行约束。

3.3. 建图
在建图部分包含稀疏地图以及平面实例网格地图。其中稀疏地图有点、线以及面的特征组成。建图的策略跟其他经典SLAM类似,即将新观测到的点线面特征保存在局部地图中,然后将质量较高的特征放入全局地图中。这里注意一点就是不同于点、线特征,对于面特征来说我们对于新检测到的面特征在插入到全局地图之前我们需要先检查一下当前面特征是否与已观测到的平面相关联,若关联则将其加入到相关联平面中,否则就以新的平面插入到地图中。

4. 实验验证
作者在与其他SLAM系统进行对比时,选择将回环检测模块关闭来进行对比,取得了不错的实验效果,下面我将在ICL-NUM数据集上同ORB-SLAM2进行对比实验。


误差对比分析针对ICL-NUM的living_room_traj0_frei_png以及traj3_frei_png这两个数据集进行了测试,做了绝对轨迹误差(ape)分析,结果如下所示:
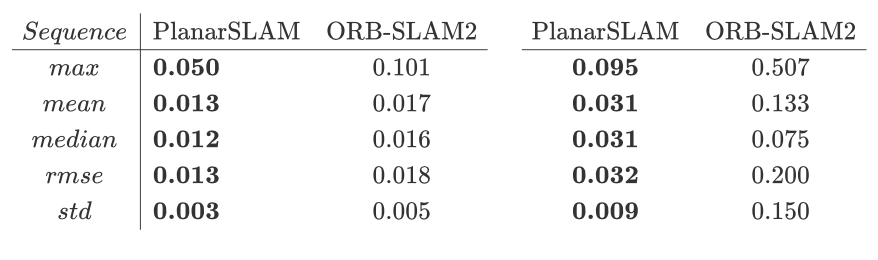
表的左半部分为living_room_traj0_frei_png分析结果,右半部分为traj3_frei_png分析结果。

planar SLAM
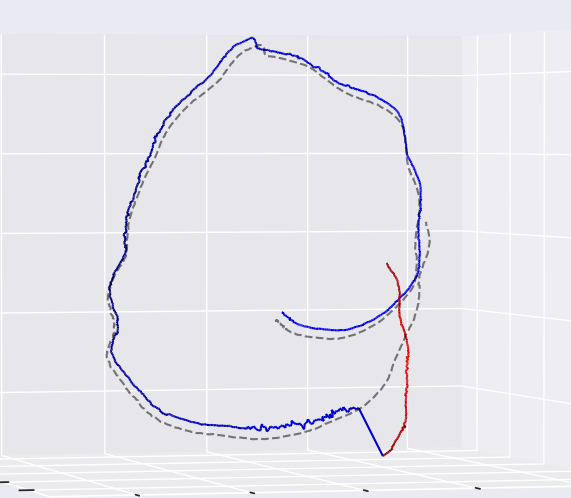
上图为在traj3_frei_png数据集上测试的相机轨迹。
通过在数据集上的实验对比发现,在弱纹理、结构化场景中,通过将线、面特征加入到ORB-SLAM2的框架中,可以有效的为SLAM位姿提供强有力的约束,提升了SLAM系统的稳定性及精度,但同时由于加入面和线特征的缘故,会增加系统计算资源的投入。由于没有真值进行对比,仅将小车的运动轨迹显示出来。
下面为在走廊环境下的实验效果:
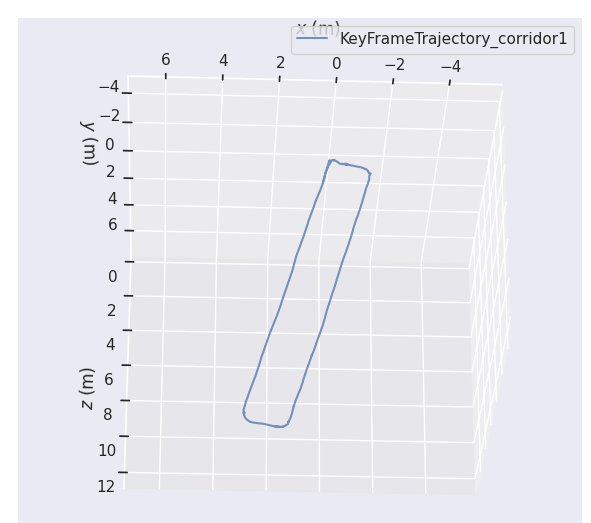
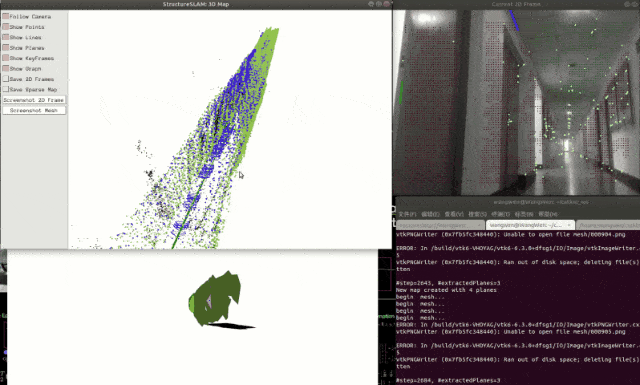
通过实际测试效果来看,Planar在走廊基本实现对自身位姿的准确估计,但在测试过程中需要注意,虽然PlanarSLAM有效的提升了在结构化弱纹理场景下的鲁棒性和精度。但在实际运行中应该避免相机直接面对一堵白墙,此时对相机来说无纹可言,无法有效提升点、线特征导致位姿估计错误。
4. 代码地址
https://github.com/yanyan-li/PlanarSLAM
参考文献
PlanarSLAM:基于结构化约束的视觉SLAM_深蓝学院的博客-CSDN博客_结构化slam
Structure-SLAM: Low-Drift Monocular SLAM in Indoor Environments
RGB-D SLAM with Structural Regularities