前言

树是一种非线性数据结构，它由若干个节点和边组成。每个节点都有一个值，而边则表示节点之间的关系。树具有层次结构，其中一个节点被称为根节点，它没有父节点。除根节点外，每个节点都有且仅有一个父节点。树的基本性质包括树的深度、高度、度数等。

森林是由若干棵互不相交的树组成的集合。一棵树可以看作是一个仅包含一棵树的森林。

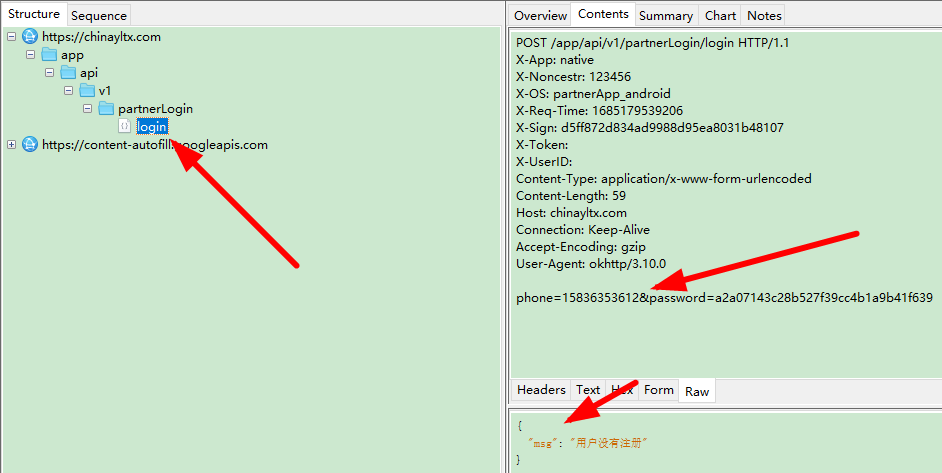
二叉树是一种特殊的树，它的每个节点最多只有两个子节点，分别称为左子节点和右子节点。二叉树是树的一种特殊形式，它具有树的所有基本性质，同时还有一些独特的性质。下图为一个树的结构示意：
在这里插入图片描述
因为B节点的度为3，所以上图是树结构但不是二叉树结构。二叉树在树型数据结构中是非常重要的一部分，很多实际问题抽象后的结构往往是二叉树形式的。

一、二叉树的基本定义

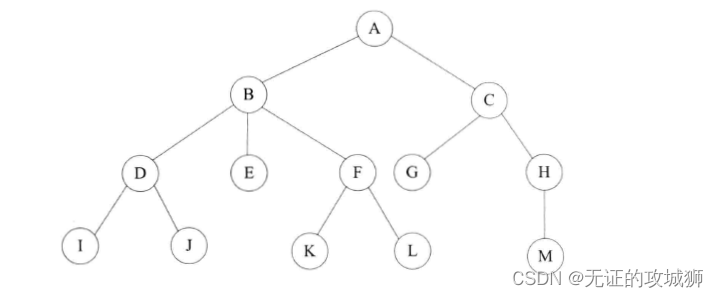
二叉树结构在数学中可以用一个有限的集合来表示。这里我们可以用图形的方式来展示二叉树的结构，如下图所示：

在这里插入图片描述

上图表示了二叉树的基本性质，它每个节点最多有两个子节点，可以称度为2，没有分支节点的4、5、6、7可以称之为叶子节点。1节点没有上一层节点，我们称之为根节点，它没有父节点。2节点的度为2，它是一个分支节点，它也是4、5节点的父节点。上图的二叉树有三层，所以我们称之高度或深度为3。

如上所述，学习二叉树，我们先要明白一些常用的术语：

树的度：树中所有节点的度的最大值。度是指一个节点拥有的子节点的个数，明显二叉树的度为2。
节点的度：一个节点拥有的子节点的个数，同上二叉树的节点度为2。
树的高度：也称深度，树中所有节点的层次的最大值。根节点所在的层定义为第一层，它的子节点所在的层为第二层，以此类推。因此，一棵只有一个节点（即根节点）的树的高度为1，而一棵空树（没有节点）的高度为0。上图的二叉树高度为3。
分支节点：度大于零的节点。
叶子节点：度为零的节点。
空树：没有任何节点的树。
完全二叉树：除叶子节点外，每一层的结点都达到最大个数。就是除叶子节点层外，每一个节点都有2个分支节点。

这些术语有助于我们理解和分析二叉树的性质和操作。

二、二叉树的基本性质

对于二叉树，有很多已证明的特性，其中又有几项比较重要的特性我们一定要明白（以下均在非空二叉树条件下）：

第 x 层最多有 2^x-1个节点。推而广之，深度为 k 的二叉树最多有2^k - 1 个节点。
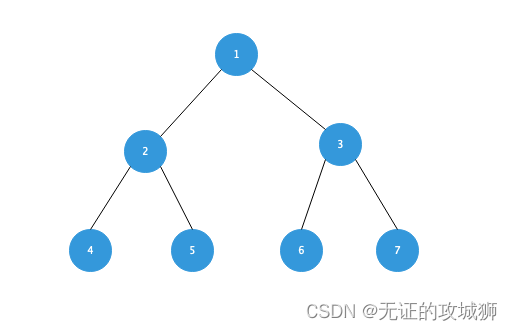
具有 n 个节点的完全二叉树的深度 k = n/2 。如上图所示，节点数是n=7，所以深度k为7/2=3。（对于C++的整数类型，这个公式是成立的，对于python这种弱类型语言应该描述成7//2）
对于完全二叉数，我们以 i 表示节点序号，如上图，i 从上至下，从左至右编号。那么这个完全二叉树满足以下性质：
1、如果i > 1，那么它的父节点为 i/2 （整除）。
2、于上一点相反，如果一个节点存在分支节点，那么它的左子节点为 2i，右子节点为2i + 1。
3、上一点继续推导可以得出，如果2i > n 那么这个结点没有分支节点，它是一个叶子节点。
如果 2i + 1 > n 那么这个结点没有右分支节点。
如果2i == n，这个二叉树就不是完全二叉树。

为什么要搞这些数学公式呢？因为根据这些特性，我们可以把二叉树的存储简化到一个数组就完成了。我们可以假设任一二叉树为完全二叉树，不存在的节点，我们以-1表示，当然也可以用0表示，根节点我们定义为 1，如此我们可以根据以上性质，在一个数组中存储二叉树，以节点编号为数组下标即可！

它非常的方便！并且父节点、左右子节点都可以根据公式得到，是双向可访问的。继续以上图的完全二叉树为例，我们来看看如何在一个数组中存储这个二叉树：
在这里插入图片描述

三、二叉树的存储（数组）

如上图所示，稍一计算便明白，它符合我们前面所述的特性。这种存储方式简直太方便了。我们只需在不存在的下标填0，这可以在数组生成时同步完成。其它下标填入相应数据即可，最大的优点就是可以随机存取任一个节点，这是采用链式存储所不能办到的，必须遍历。当然它的缺点也明显，如果不是完全二叉树，特别是一些歪脖子树，这种方式很浪费空间，如果数据规模很大，可能难以在内存中找到这么大块的连续空间。
下面我们用代码实现这个存储方式：

#include <iostream>
using namespace std;

const int MAX_SIZE = 100;   //数组最大容量
int tree[MAX_SIZE];         //存储二叉树的数组
int n;                      //节点个数

//前序遍历
void preOrder(int root){
    if (root > n) return;      //超出范围，返回
    cout << tree[root] << " "; //访问根节点
    preOrder(root * 2);        //访问左子树
    preOrder(root * 2 + 1);    //访问右子树
}

//中序遍历
void inOrder(int root){
    if (root > n) return;        //超出范围，返回
    inOrder(root * 2);          //访问左子树
    cout << tree[root] << " ";   //访问根节点
    inOrder(root * 2 + 1);      //访问右子树
}

以上是用了递归遍历的方法，递归遍历是一种简单直观的方法，它利用了递归函数调用自身的特性来遍历树中的节点。非递归遍历则需要使用栈或队列等数据结构来辅助遍历。

至于没给出的后序遍历只是改一下代码的顺序，层序遍历更是只要从1到n遍历数组即可。那真是相当的方便啊~，不过看起来一点二叉树的感觉都没有，作者你是不是在忽悠人啊？哈哈…面向对象的编程就是这么的抽象，心中有树，它就是树。

总结

首先笔者没有忽悠人，这确实是二叉树的存储办法，而且是挺好的一个方法。当然在实际工作中它较少被使用，这种存储方式在工作中可以用于排序二叉树（也称二叉搜索树、有序二叉树）它可以用来实现高效的查找和排序算法，比如堆排序。此外，数组存储二叉树的方式也可以用于实现堆数据结构，如大顶堆和小顶堆，它们常用于实现优先队列等数据结构。

嗯这字数已经够多了，也写累了，链表都写了两篇才完成，二叉树只会更多，下一篇写二叉树的链式存储方式及实用示例。