一、线性回归算法简介

1.解决回归问题；
2.思想简单，实现容易；
3.是许多强大的非线性模型的基础；
4.结果具有很好的可解释性；
5.蕴含机器学习中的很多重要思想；
样本特征x只有一个称为简单的线性回归；

不用绝对值是因为其不能保证在之后的算法中处处可导；
因此我们选择了真值与预测值差之平方来表示偏差；
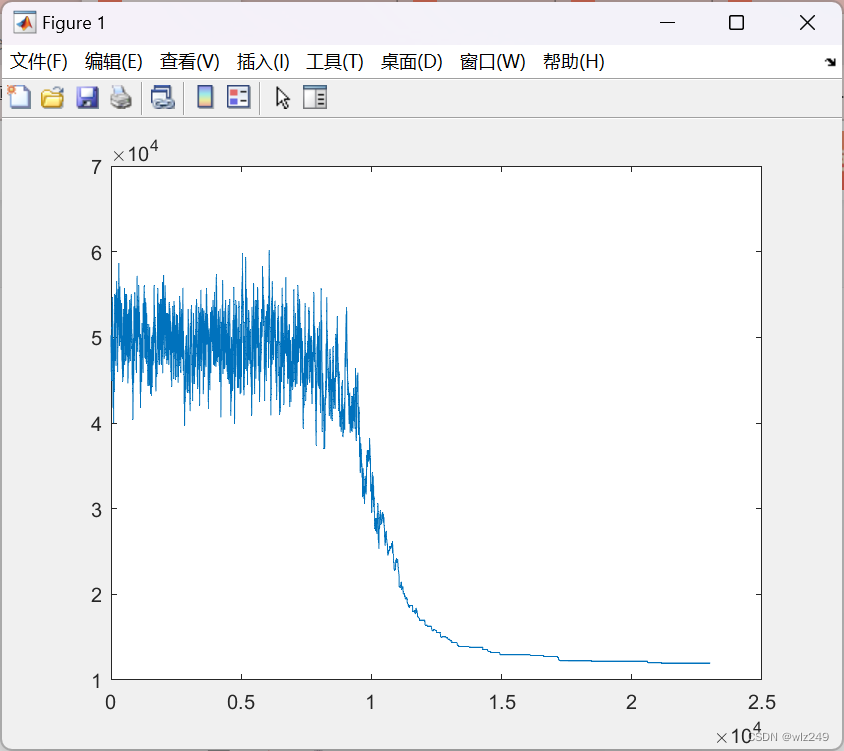
推出来这个式子之后我们的目标就是使其尽可能地小；
——

典型的最小二乘法的问题

目标：

其实就是找到一个模型最大程度拟合我们的数据，在线性回归算法中这个模型就是一个线性回归方程，在这里，我们称下图目标函数为损失函数（loss function）也就是说度量出模型没有拟合样本的损失的那一部分
有的函数中度量的是拟合的那部分函数，称为效用函数（utility function）

不管是哪一种函数，我们的机器学习都是通过分析问题，确定问题的损失函数或者效用函数，通过最优化损失函数或者效用函数获得机器学习的模型；
近乎所有参数学习算法（线性回归，多项式回归，逻辑回归，svm，神经网络等）都是这样的思路；

具体怎么推此处省略

二、简单线性回归的实现

三、向量化运算

（使用向量运算比使用for循环速度是更快的）结果基本大小一样