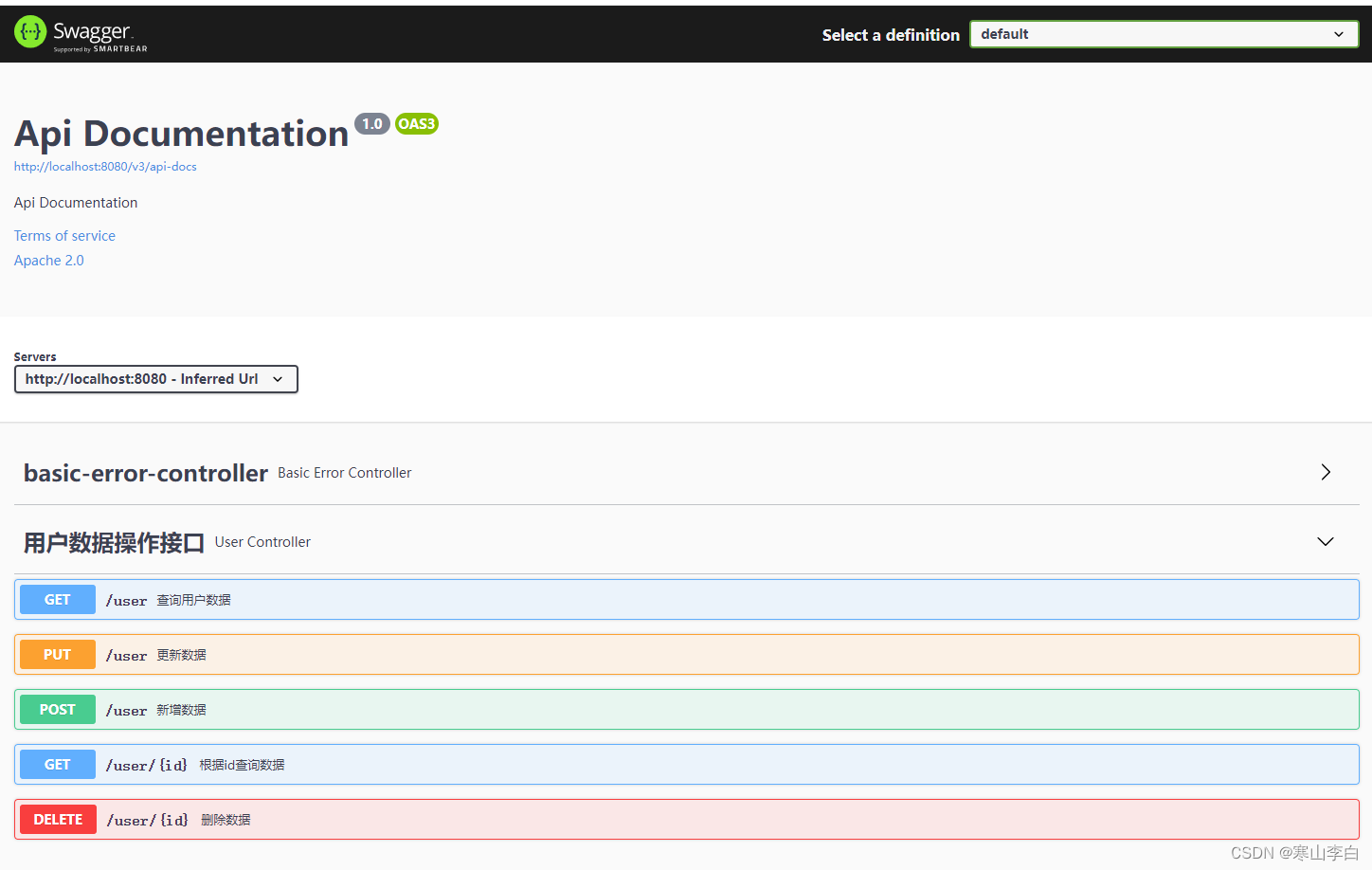
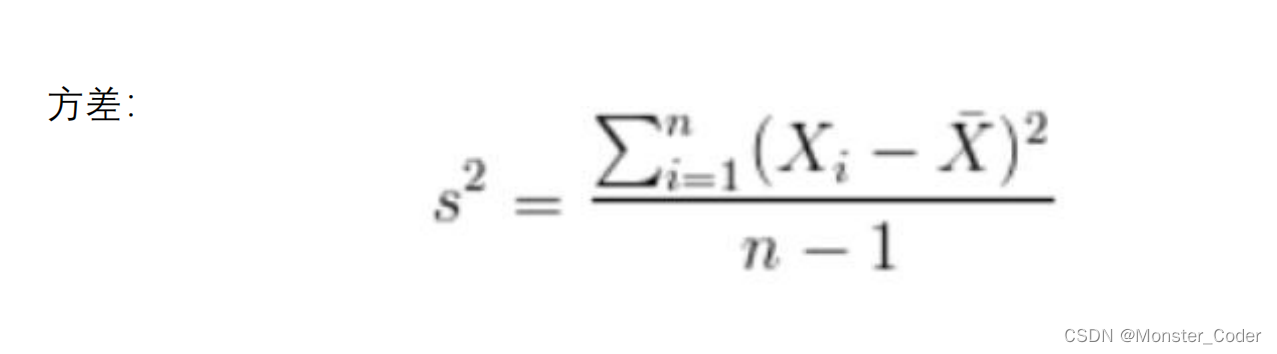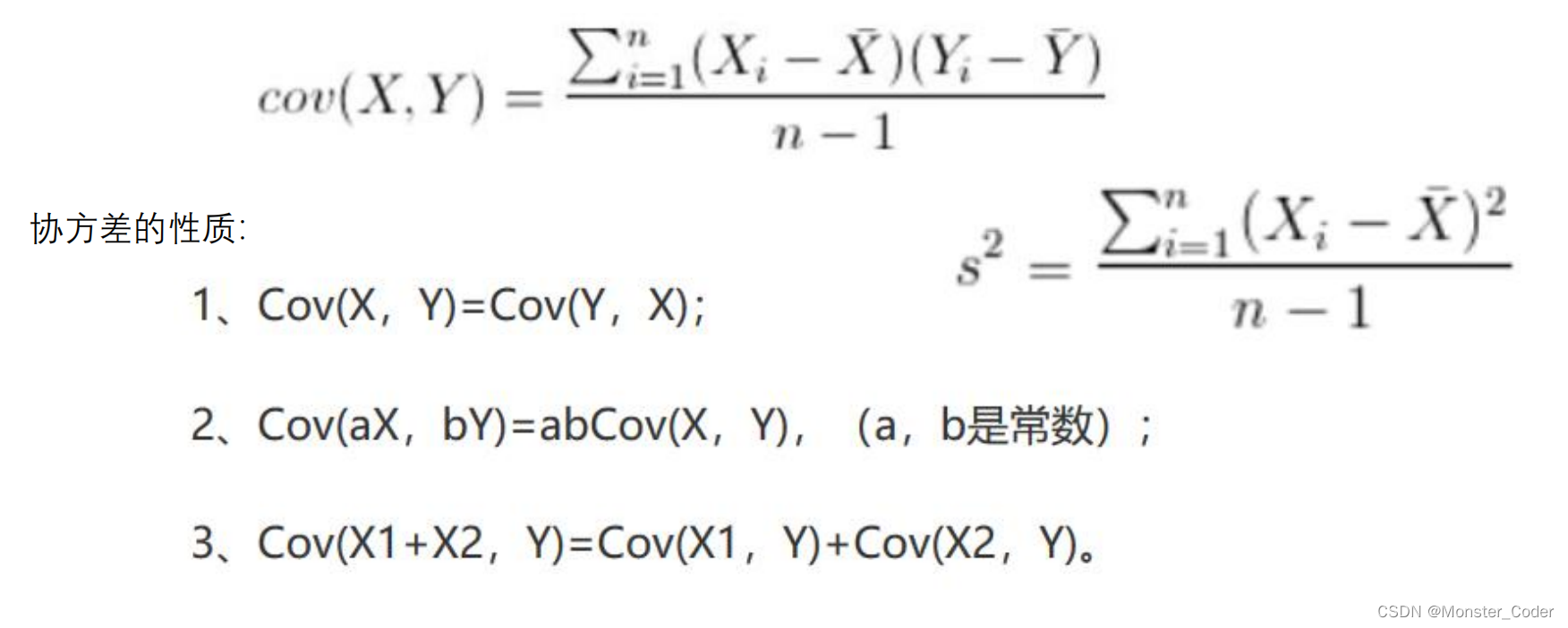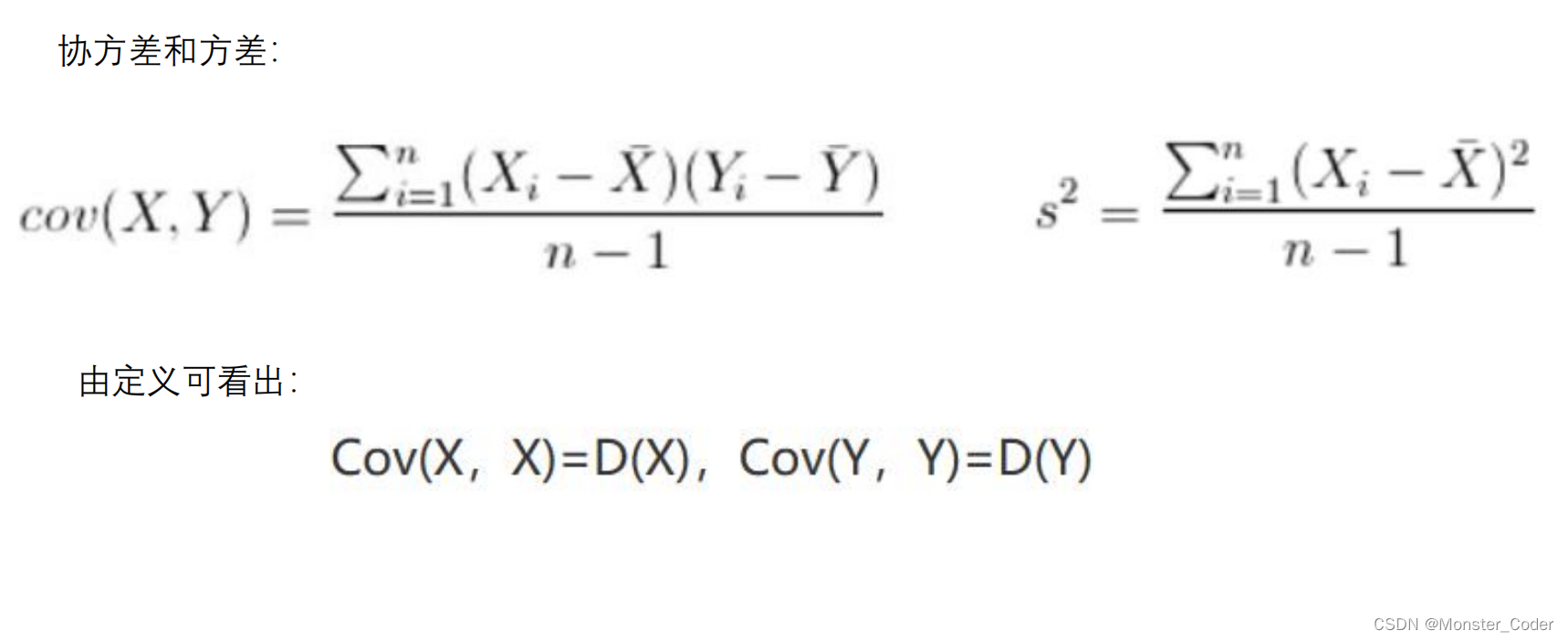特征

什么是特征：

举个例子：一个妹子很好看，好看的在哪里？腿长（特征1），白（特征2），性格开朗（特征3）

那么可以概括为好看妹子的特征是[腿长，白，性格开朗]

特征类型：

• 相关特征：对于学习任务（例如分类问题）有帮助，可以提升学习算法的效果

比如：腿长，白

• 无关特征：对于我们的算法没有任何帮助，不会给算法的效果带来任何提升

比如：性格好（性格好的妹子不一定好看，好看的妹子不一定性格好）

• 冗余特征：不会对我们的算法带来新的信息，或者这种特征的信息可以由其他的特征推断出

比如：腿长可以推导出身高高

为什么要进行特征提取：

• 降维

• 降低学习任务的难度

• 提升模型的效率

什么是特征选择：

从N个特征中选择其中M（M<=N）个子特征，并且在M个子特征中，准则函数可以达到最优解。

特征选择想要做的是：选择尽可能少的子特征，模型的效果不会显著下降，并且 结果的类别分布尽可能的接近真实的类别分布。

怎么做特征选择：

1. 生成过程：生成候选的特征子集；

2. 评价函数：评价特征子集的好坏；

3. 停止条件：决定什么时候该停止；

4. 验证过程：特征子集是否有效；

特征选择生成过程：

生成过程是一个搜索过程，这个过程主要有以下三个策略：

1. 完全搜索 ：根据评价函数做完全搜索。完全搜索主要有两种：穷举搜索和非穷举搜索;

2. 启发式搜索 ：根据一些启发式规则在每次迭代时，决定剩下的特征是应该被选择还是被拒绝。这种方法很简单并且速度很快。

3. 随机搜索 ：每次迭代时会设置一些参数，参数的选择会影响特征选择的效果。由于会设置一些参数（例如最大迭代次数）。

特征选择停止条件：

停止条件用来决定迭代过程什么时候停止，生成过程和评价函数可能会对于怎么选择停止条件产生影响。停止条件有以下四种选择：

1. 达到预定义的最大迭代次数；

2. 达到预定义的最大特征数；

3. 增加（删除）任何特征不会产生更好的特征子集；

4. 根据评价函数，产生最优特征子集；

特征选择评价函数：

评价函数主要用来评价选出的特征子集的好坏， 一个特征子集是最优的往往指相对于特定的评价函 数来说的 。评价函数主要用来度量一个特征（或者特征子集）可以区分不同类别的能力。根据具体的评价方法主要有三类：

• 过滤式（ filter): 先进行特征选择，然后去训练学习器，所以特征选择的过程与学习器无关。相当于先对于特征进行过滤操作，然后用特征子集来训练分类器。对每一维的特征“打分”，即给每一维的特征赋予权重，这样的权重就代表着该维特征的重要性，然后依据权重排序。

• 包裹式（ wrapper）： 直接把最后要使用的分类器作为特征选择的评价函数，对于特定的分类器选择最优的特征子集。将子集的选择看作是一个搜索寻优问题，生成不同的组合，对组合进行评

价，再与其他的组合进行比较。这样就将子集的选择看作是一个优化问题，

• Filter和Wrapper组合式算法： 先使用Filter进行特征选择，去掉不相关的特征，降低特征维度；然后利用Wrapper进行特征选择。

• 嵌入式（ embedding）： 把特征选择的过程与分类器学习的过程融合一起，在学习的过程中进行特征选择。

其主要思想是：在模型既定的情况下学习出对提高模型准确性最好的属性。是讲在确定模型的过程中，挑选出那些对模型的训练有重要意义的属性。

特征选择评价函数：

1. 距离度量：如果 X 在不同类别中能产生比 Y 大的差异，那么就说明 X 要好于 Y;

2. 信息度量：主要是计算一个特征的信息增益（度量先验不确定性和期望, 后验不确定性之间的差异）；

3. 依赖度量：主要用来度量从一个变量的值预测另一个变量值的能力。最常见的是相关系数：

用来发现一个特征和一个类别的相关性。如果 X 和类别的相关性高于 Y与类别的相关性，那么X优于Y。对相关系数做一点改变，用来计算两个特征之间的依赖性，值代表着两个特征之间的冗余度。

4. 一致性度量：对于两个样本，如果它们的类别不同，但是特征值是相同的，那么它们是不一致的；否则是一致的。找到与全集具有同样区分能力的最小子集。严重依赖于特定的训练集和最小特征偏见（Min-Feature bias）的用法；找到满足可接受的不一致率（用户指定的参数）的最小规模的特征子集。

5. 误分类率度量：主要用于Wrapper式的评价方法中。使用特定的分类器，利用选择的特征子集来预测测试集的类别，用分类器的准确率来作为指标。这种方法准确率很高，但是计算开销较大。

特征选择算法：

完全搜索:

广度优先搜索（ Breadth First Search）： 主要采用完全搜索策略和距离度量评价函数。使用广度优先算法遍历所有可能的特征子集，选择出最优的特征子集。 主要采用完全搜索和距离度量。 B&B从所有的特征上开始搜索，每次迭代从中去掉一个特征，每次给评价函数的值一个限制条件。因为评价函数满足单调性原理（一个特征子集不会好于所有包含这个特征子集的更大的特征子集），所以如果一个特征使得评价函数的值小于这个限制，那么就删除这个特征。类似于在穷举搜索中进行剪枝。

定向搜索（ Beam Search）： 主要采用完全搜索策略和误分类率作为评价函数。选择得分最高的特征作为特征子集，把它加入到一个有长度限制的队列中，从头到尾依次是性能最优到最差的特征子集。每次从队列总取得分最高的子集，然后穷举向该子集中加入一个特征后所有的特征集，按照得分把这些子集加入到队列中。

最优优先搜索（ Best First Search）： 和定位搜索类似，不同点在于不限制队列的长度。

启发式搜索:

序列前向选择（ SFS , Sequential Forward Selection） ：使用误分类率作为评价函数。从空集开始搜索，每次把一个特征加入到这个特征子集中，使得评价函数达到最优值。如果候选的特征子集不如上一轮的特征子集，那么停止迭代，并将上一轮的特征子集作为最优的特征选择结果。

广义序列前向选择（ GSFS ，Generalized Sequential Forward Selection）： 该方法是SFS算法的加速算法，它可以一次性向特征集合中加入r个特征。在候选特征中选择一个规模为r的特征子集，使得评价函数取得最优值。

序列后向选择（ SBS , Sequential Backward Selection）： 把误分类率作为评价函数。从特征的全集开始搜索，每次从特征子集中去掉一个特征，使得评价函数达到最优值。

广义序列后向选择（ GSBS，Generalized Sequential Backward Selection）： 该方法是SBS的加速，可以一次性的从特征子集中去除一定数量的特征。是实际应用中的快速特征选择算法，性能相对较好。但是有可能消除操作太快，去除掉重要的信息，导致很难找到最优特征子集。

双向搜索（ BDS , Bi-directional Search）： 分别使用SFS和SBS同时进行搜索，只有当两者达到一个相同的特征子集时才停止搜索。为了保证能够达到一个相同的特征子集，需要满足两个条件：

被SFS选中的特征不能被SBS去除；

被SBS去除的特征就不能SFS选择；

增L去R选择算法（ LRS , Plus L Minus R Selection）：

采用误分类率作为评价函数。允许特征选择的过程中进行回溯，这种算法主要有两种形式：

当L>R时，是一种自下而上的方法，从空集开始搜索，每次使用SFS增加L个特征，然后用SBS从中去掉R个特征；

当L<R时，是一种自上而下的算法，从特征的全集开始搜索，每次使用SBS去除其中的R个特征，使用SFS增加L个特征；

序列浮动选择（ Sequential Floating Selection）： 和增L去R算法类似，只不过序列浮动算法的L和R不是固定的，每次会产生变化，这种算法有两种形式：

序列浮动前向选择（ SFFS , Sequential Floating Forward Selection）: 从空集开始搜索，每次选择一个特征子集，使得评价函数可以达到最优，然后在选择一个特征子集的子集，把它去掉使得评价函数达到最优；

序列浮动后向选择（ SFBS , Sequential Floating Backward Selection： 从特征全集开始搜索，每次先去除一个子集，然后在加入一个特征子集。

决策树算法（DTM , Decision Tree Method） ：采用信息增益作为评价函数。在训练集中使用C4.5算法，等到决策树充分增长，利用评价函数对决策树进行剪枝。最后，出现在任意一个叶子

节点的路径上的所有特征子集的并集就是特征选择的结果。

随机搜索:

LVF（Las Vegas Filter）：使用一致性度量作为评价函数。使用拉斯维加斯算法随机搜索子集空间，这样可以很快达到最优解。对于每一个候选子集，计算它的不一致性，如果大于阈值，则去除这个子集。否则，如果这个候选子集中的特征数量小于之前最优子集的数量，则该子集作为最优子集。这个方法在有噪声的数据集达到最优解，它是很简单被实现而且保证产生比较好的特征子集。但是在一些特定问题上，它会花费比启发式搜索更多的时间，因为它没有利用到先验知识。

遗传算法:

使用误分类率作为评价函数。随机产生一批特征子集，然后使用评价函数对于子集进行评分，通过选择、交叉、突变操作产生下一代特征子集，并且得分越高的子集被选中产生下一代的几率越高。经过N代迭代之后，种群中就会形成评价函数值最高的特征子集。它比较依赖于随机性，因为选择、交叉、突变都由一定的几率控制，所以很难复现结果。遗传算法的过程如下：

1. 随机产生初始种群；

2. 在非支配排序后，通过遗传算法的三个算子（选择算子，交叉算子，变异算子）进行变更操作得到第一代种群；

3. 将父代种群与子代种群合并得到大小为N的初始化种群；

4. 对包括N个个体的种群进行快速非支配排序；

5. 对每个非支配层中的个体进行拥挤度计算；

6. 根据非支配关系及个体的拥挤度选取合适的个体组成新的父代种群；

7. 通过遗传算法的基本变更操作产生新的子代种群；

8. 重复 3 到 7 直到满足程序结束的条件（即遗传进化代数）；

特征提取：

特征是什么：

常见的特征有边缘、角、区域等。

特征提取：

是通过属性间的关系，如组合不同的属性得到新的属性，这样就改变了原来的

特征空间。

特征选择：

是从原始特征数据集中选择出子集，是一种包含的关系，没有更改原始的特征空间。

目前图像特征的提取主要有两种方法：传统图像特征提取方法和深度学习方法。

1. 传统的特征提取方法：基于图像本身的特征进行提取；

2. 深度学习方法：基于样本自动训练出区分图像的特征分类器；

特征选择（feature selection）和特征提取（Feature extraction）都属于降维（Dimension reduction）

特征提取：

特征提取的主要方法：

主要目的是为了排除信息量小的特征，减少计算量等：

主成分分析（ PCA）

将数据从原始的空间中转换到新的特征空间中，例如原始的空间是三维的(x,y,z)，x、y、z分别是原始空间的三个基，我们可以通过某种方法，用新的坐标系(a,b,c)来表示原始的数据，那么a、b、c就是新的基，它们组成新的特征空间。在新的特征空间中，可能所有的数据在c上的投影都接近于0，即可以忽略，那么我们就可以直接用(a,b)来表示数据，这样数据就从三维的(x,y,z)降到了二维的(a,b)。

问题是如何求新的基(a,b,c)?

一般步骤是这样的：

1. 对原始数据零均值化（中心化），

2. 求协方差矩阵，

3. 对协方差矩阵求特征向量和特征值，这些特征向量组成了新的特征空间。

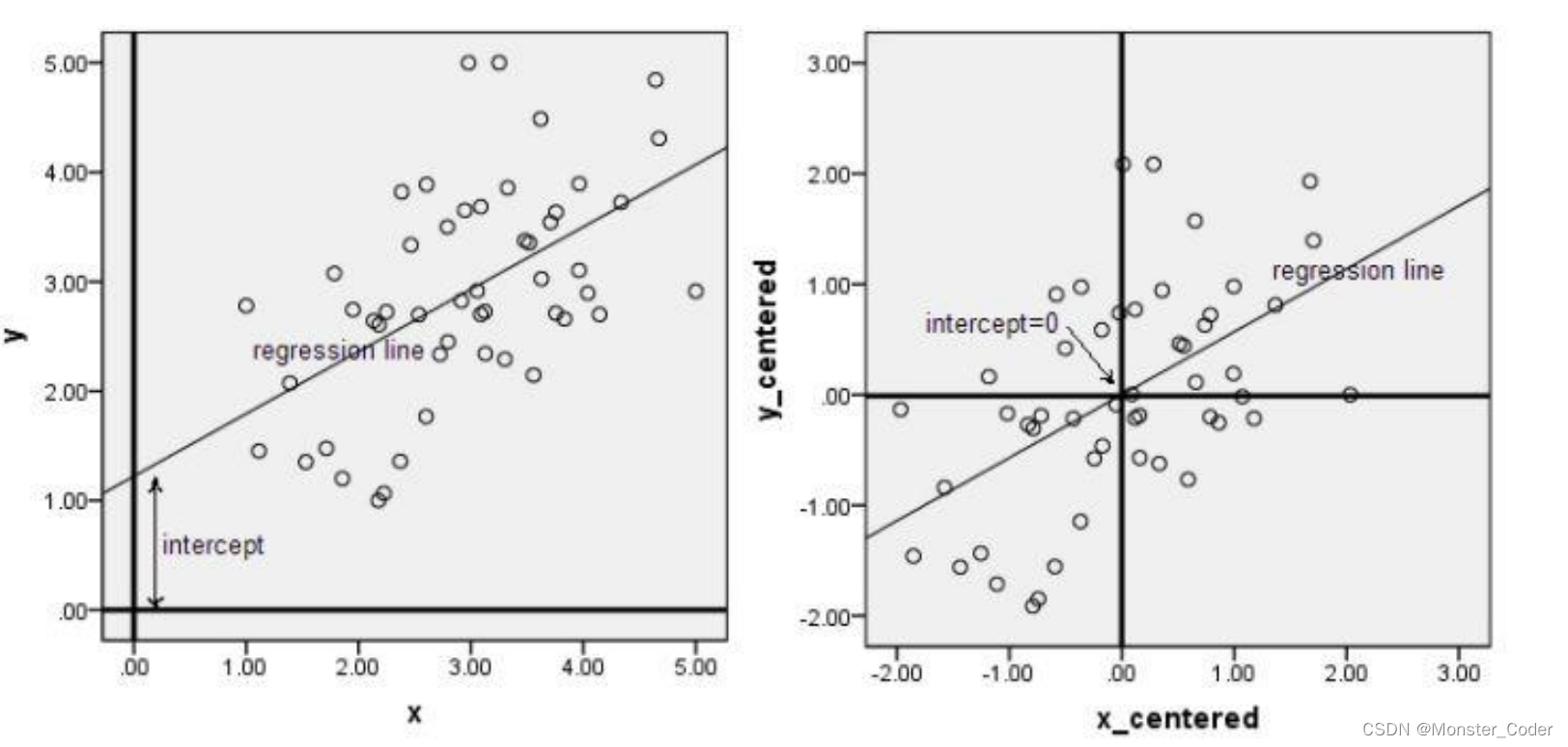
PCA--零均值化（中心化）：

中心化即是指变量减去它的均值，使均值为0。

其实就是一个平移的过程，平移后使得所有数据的中心是(0,0)

只有中心化数据之后，计算得到的方向才能比较好的“概括”原来的数据。

此图形象的表述了，中心化的几何意义，就是将样本集的中心平移到坐标系的原点O上。

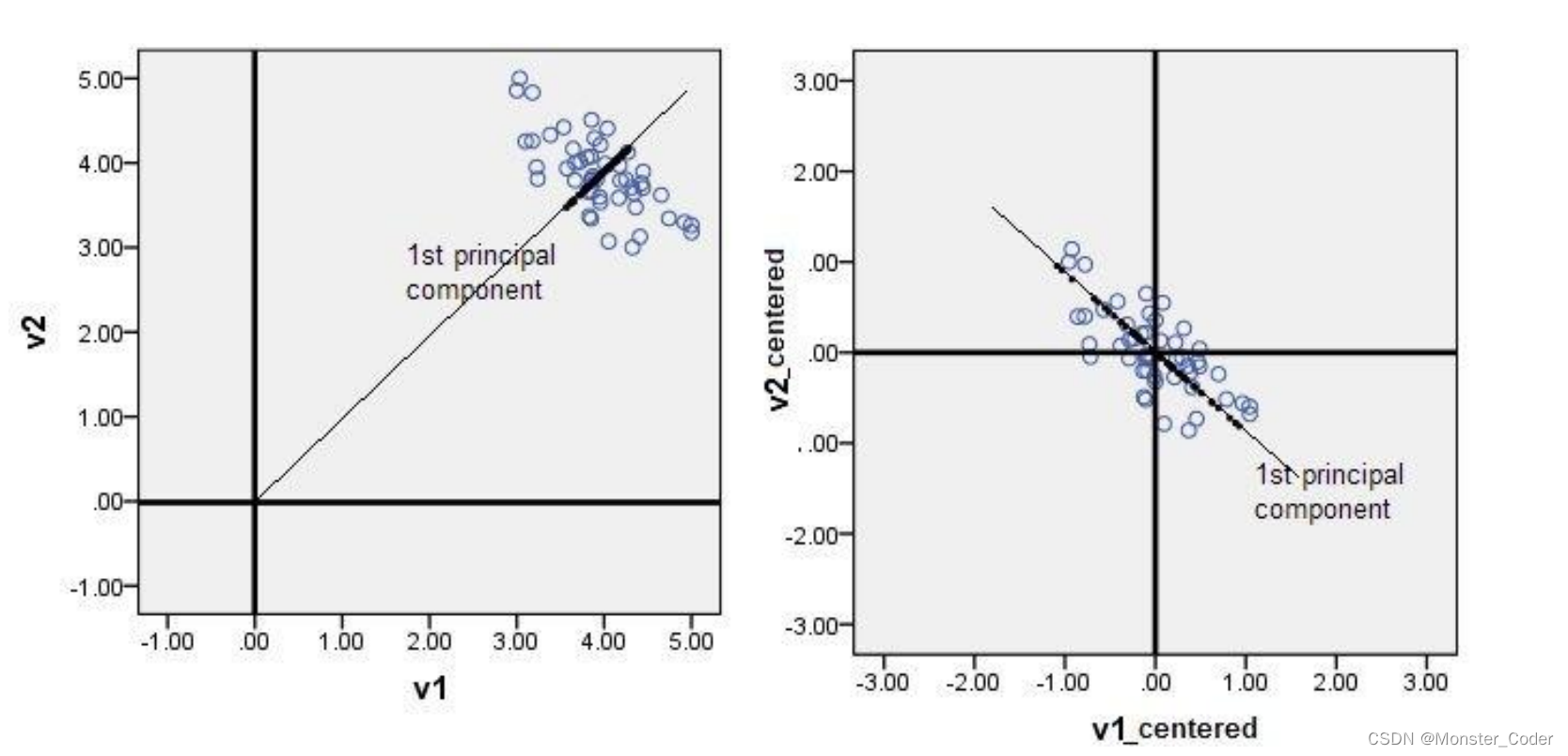
PCA降维的几何意义：

如果它在某一坐标轴上的方差越大，说明坐标点越分散，该属性能够比较好的反映源数据。

PCA算法的优化目标就是 :

① 降维后同一维度的方差最大

② 不同维度之间的相关性为0

PCA--协方差

协方差就是一种用来度量两个随机变量关系的统计量。

同一元素的协方差就表示该元素的方差，不同元素之间的协方差就表示它们的相关性。

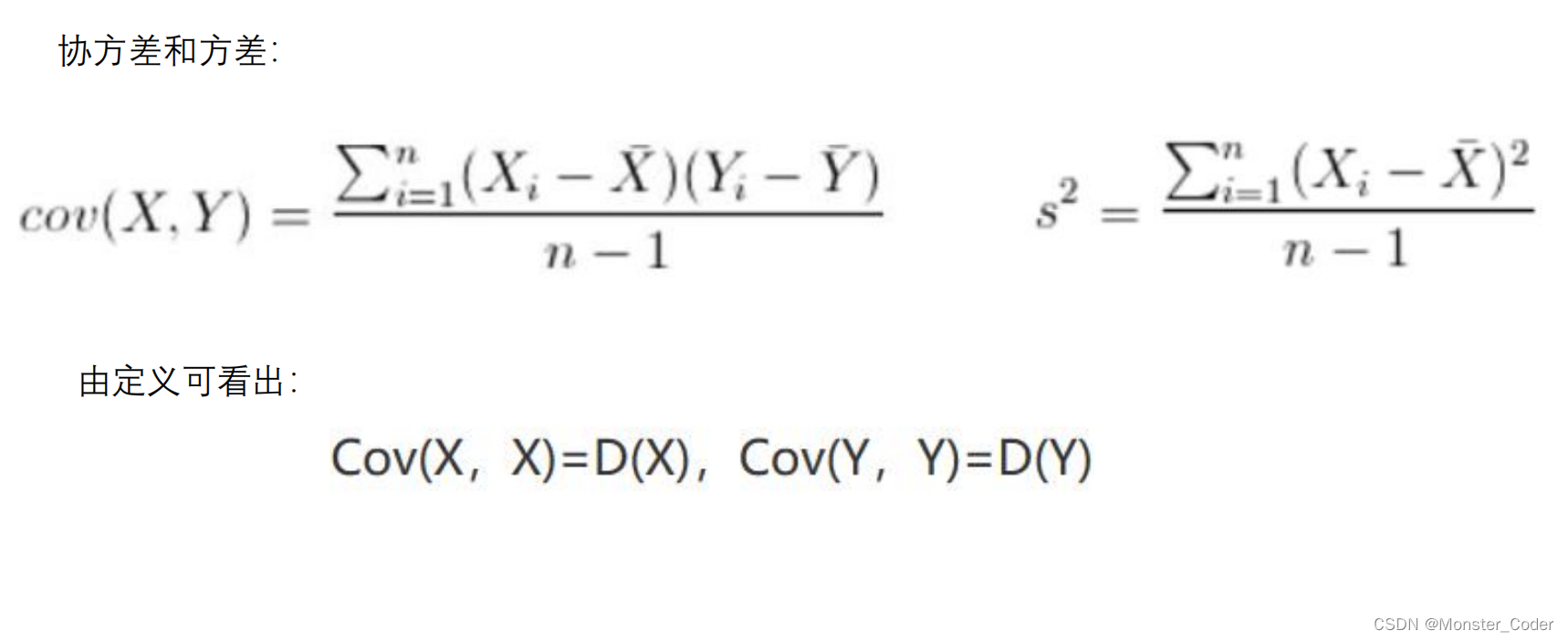
对协方差矩阵求特征值、特征矩阵

对特征值进行排序

评价模型的好坏，K值的确定

累了吧（不累？反正我累了），上代码！

import cv2
import numpy as np

# 1. 对原始数据零均值化（中心化），
# 2. 求协方差矩阵，
# 3. 对协方差矩阵求特征向量和特征值，这些特征向量组成了新的特征空间。
class PCA:

# 求均值
def centralization(array):
return np.array([np.mean(attr) for attr in array.T])

# 中心化矩阵
def getCentralizationMatrix(array):
mean = PCA.centralization(array)
print("均值:" , mean)
return array - mean

# 协方差矩阵
def getCov(array):
centerMatrix = PCA.getCentralizationMatrix(array)
length = len(centerMatrix)
print("中心矩阵:" , centerMatrix)
return np.dot(centerMatrix.T , centerMatrix) / (length - 1)

# 获取特征值
def getEigenValue(array):
# length = len(array)
# identityMatrix = PCA.initIdentityMatrix(length)
cov = PCA.getCov(array)
print("协方差矩阵:" , cov)
a, b = np.linalg.eig(cov)
print("特征值:" , a)
print("特征值向量" , b)
return a , b

def getEigenArray(array , size):
value , eArray = PCA.getEigenValue(array)
length = len(np.sort(value))
# 取前几行(自定义)
newArray = np.array([eArray[:,i] for i in range(size)])
return newArray.T

# 获取降维矩阵
def dimensionalityReductionMatrix(array , size):
eArray = PCA.getEigenArray(array , size)
print("特征矩阵" , eArray)
return np.dot(array , eArray)

# # 创建单位矩阵
# def initIdentityMatrix(length):
# array = [[0] * length] * length
# for i in range(length):
# for j in range(length):
# if(i == j):
# array[i][j] = 1
# else:
# continue
# return array

def getImageArray(filePath):
image = cv2.imread(filePath, 1)
# 长，宽，通道
originArray = image.shape[1]

def mainFunction(filePath , size):
# imageArray = PCA.getImageArray(filePath)
# 每行就是一个样本，每列就是样本的某一个属性
imageArray = np.array([[10, 15, 29],
[15, 46, 13],
[23, 21, 30],
[11, 9, 35],
[42, 45, 11],
[9, 48, 5],
[11, 21, 14],
[8, 5, 15],
[11, 12, 21],
[21, 20, 25]])
finalArray = PCA.dimensionalityReductionMatrix(imageArray , size)
print("降维矩阵:" , finalArray)

PCA.mainFunction("111" , 2)