题意理解和二叉树表示

给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换变成T2，则称两棵树是“同构”的。

eg1：现请你判断如下两棵树（左侧为T1，右侧为T2）是否为同构树？

显然T1可以通过有限次左右孩子互换变成T2，因此这两棵树是同构的

eg2：同上

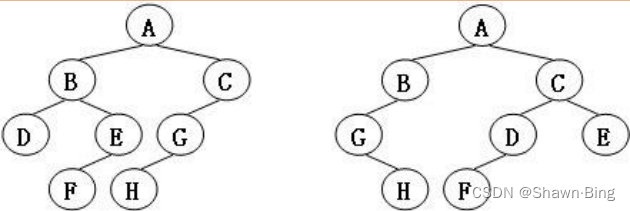
这两棵树BC子树的子结点完全不同，T1不能互换变成T2，所以不是同构

程序题目：输入两颗二叉树的信息，判断两棵树是否为同构。

输入格式:

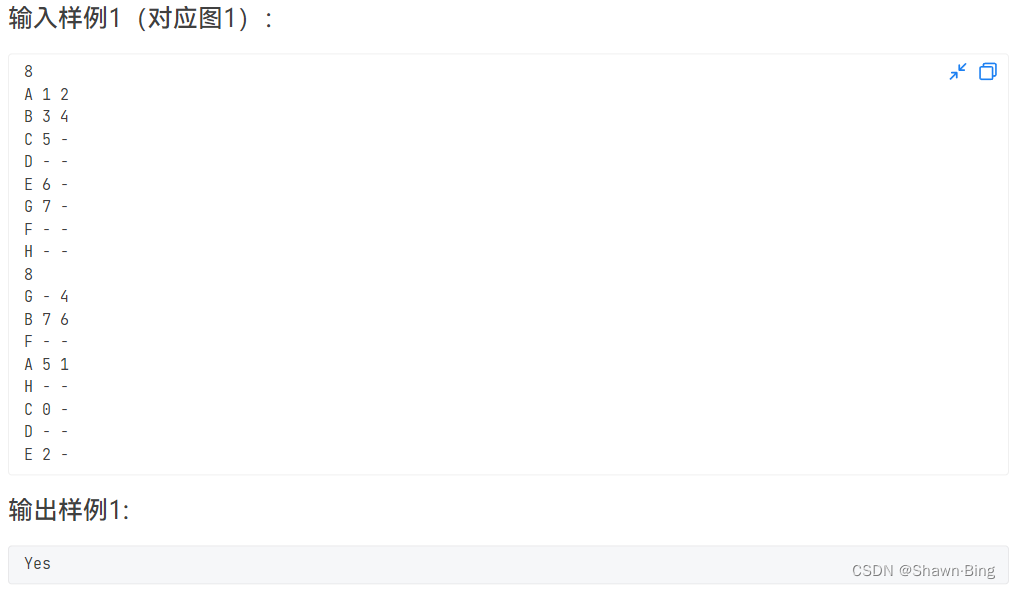
输入给出2棵二叉树树的信息。对于每棵树，首先在一行中给出一个非负整数N (≤10)，即该树的结点数（此时假设结点从0到N−1编号）；随后N行，第i行对应编号第i个结点，给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空，则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意：题目保证每个结点中存储的字母是不同的。

输出格式:

如果两棵树是同构的，输出“Yes”，否则输出“No”。

解题思路

本题需要解决三个问题：

二叉树如何表示

一般使用链表或者数组。之前的文章提到可以使用含有一个数据域和两个指针域（一个left一个right）的结构链表来表示二叉树。或者是将二叉树视为满二叉树，无结点的地方留空，用数组表示。

讲解中使用了结构数组，又称静态链表。简单来说是将基本信息存放在数组当中，左右子树用类似链表的方式来表示。例如下面的图中二叉树使用二维数组分别存储结点位置、左右子树位置

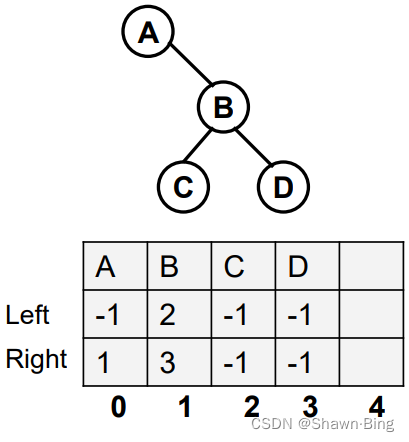
 对应结构的代码：

#define MaxTree 10
#define ElementType char
#define Tree int
#define Null -1    //传统空指针是0，而0会和下标冲突
struct TreeNode{
    ElementType Element;    
    Tree Left;
    Tree Right;
} T1[MaxTree], T2[MaxTree];

如何构造二叉树

如何从输入的若干数据中建立对应的二叉树？

程序框架搭建

int main()
{
    Tree R1, R2;
 
    R1 = BuildTree(T1);
    R2 = BuildTree(T2);
    if (Isomorphic(R1, R2)) printf("Yes\n");
    else printf("No\n");
     
    return 0;
}

Tree BuildTree( struct TreeNode T[] ){
    scanf("%d\n", &N);
    if (N) {
        //设定check来判别指向，首先都设为0
        for (i=0; i<N; i++){
            check[i] = 0;
        }
        
        for (i=0; i<N; i++) {
            //循环读入每个结点该有的三个信息
            scanf("%c %c %c\n", &T[i].Element, &cl, &cr);
            
            //若有结点A指向B，就将B的check设为1
            if (cl != '-') {
                //题目中设定为-的是没有左子树的
                T[i].Left = cl-'0';
                check[T[i].Left] = 1;
            }
            else T[i].Left = Null;

            …….. /*对cr的对应处理 */
        }
    
    //遍历结点找根结点，根结点是唯一一个没有被指向的结点，check值=0
    for (i=0; i<N; i++)
        if (!check[i]) break;
        Root = i;
    }
    return Root;
}

同构的判定

int Isomorphic ( Tree R1, Tree R2 )
{ 
    //首先判断两棵树的边界情况

    /*都是空树*/
    if ( (R1==Null )&& (R2==Null) ) 
        return 1;

    /*有一颗是空树*/
    if ( ((R1==Null)&&(R2!=Null)) || ((R1!=Null)&&(R2==Null)) )
        return 0; 

    /*根结点不同，肯定不是同构*/
    if ( T1[R1].Element != T2[R2].Element )
        return 0;

    /*两棵树都没有左子树，只判断右子树*/
    if ( ( T1[R1].Left == Null )&&( T2[R2].Left == Null ) ) 
        return Isomorphic( T1[R1].Right, T2[R2].Right );


    /*是否有一颗及以上有左子树，左子树结点数据是否一致*/
    if ( ((T1[R1].Left!=Null)&&(T2[R2].Left!=Null))&&
    ((T1[T1[R1].Left].Element)==(T2[T2[R2].Left].Element)) ) 

        /*判断左子树是否相等、右子树是否相等*/
        return ( Isomorphic( T1[R1].Left, T2[R2].Left ) &&
        Isomorphic( T1[R1].Right, T2[R2].Right ) );
 
    /*可能是A左和B右同构，交换左右子树后判别*/
    else
        return ( Isomorphic( T1[R1].Left, T2[R2].Right) &&
        Isomorphic( T1[R1].Right, T2[R2].Left ) );

}