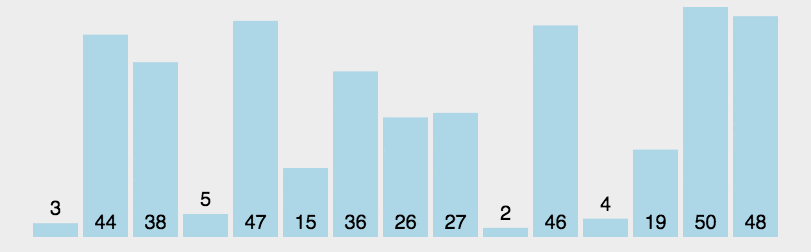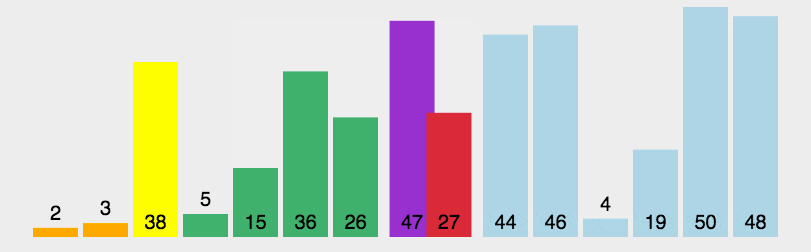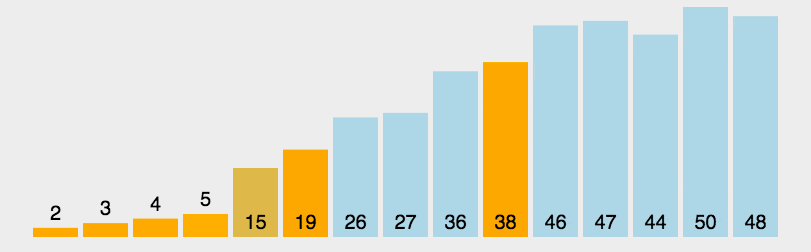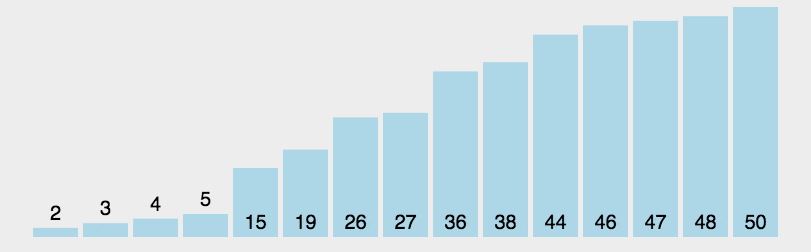
[NOIP2004 普及组] FBI 树

题目描述:

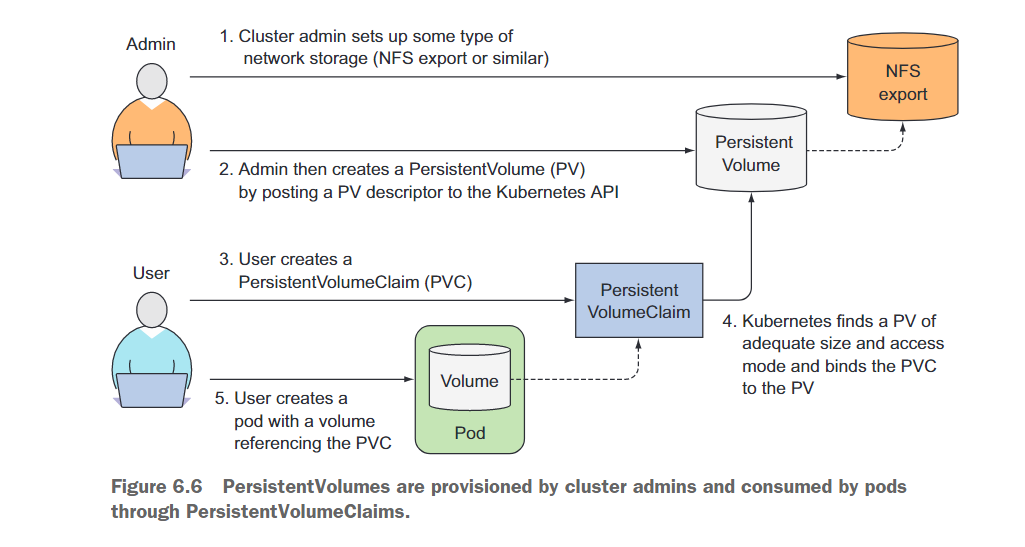
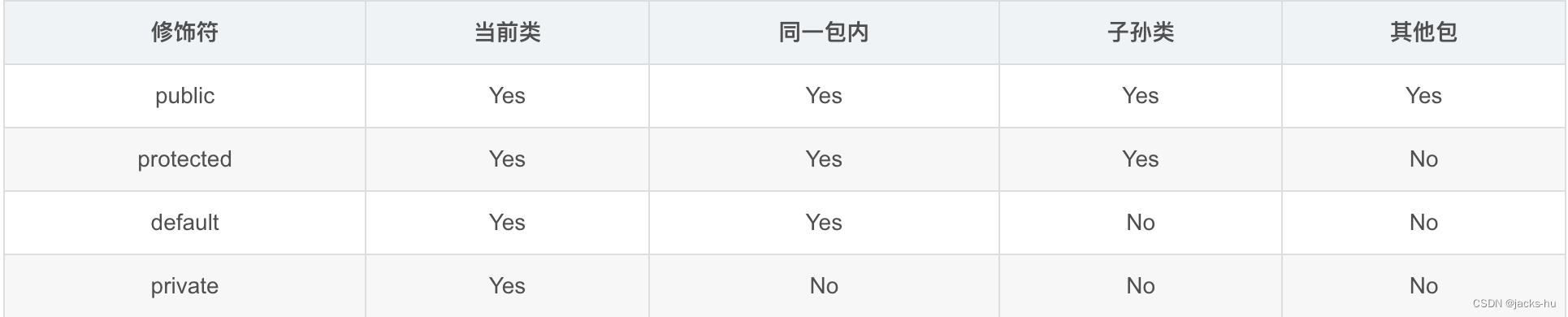
我们可以把由 0 和 1 组成的字符串分为三类：全 0 串称为 B 串，全 1 串称为 I 串，既含 0 又含 1 的串则称为 F 串。

FBI 树是一种二叉树，它的结点类型也包括 F 结点，B 结点和 I 结点三种。由一个长度为 $2^N$ 的 01 串 S 可以构造出一棵 FBI 树 T，递归的构造方法如下：

1. T 的根结点为 R，其类型与串 S 的类型相同；
2. 若串 S 的长度大于 1，将串 S 从中间分开，分为等长的左右子串 S1 和 S2；由左子串 S1 构造 R 的左子树 T1，由右子串 S2 构造 R 的右子树 T2。

现在给定一个长度为 2^N 的 01 串，请用上述构造方法构造出一棵 FBI 树，并输出它的后序遍历序列。

输入格式

第一行是一个整数 N(0≤N≤10)，

第二行是一个长度为 2^N 的 01 串。

输出格式

一个字符串，即 FBI 树的后序遍历序列。

输入输出样例

输入 #1:

3
10001011

输出 #1:

IBFBBBFIBFIIIFF

说明/提示

对于 %40% 的数据,N≤2；

对于全部的数据，N≤10。

noip2004普及组第3题。

题目大意：

题目大意就是给定一个序列，就比如10001011，我们将这个序列一直从中间分开，左边为左子树，右边为右子树，根据每一段全0全1还是10都有得到值F、B、I，构建成一棵二叉树，并且倒序输出。

队列做法：

这个解法要相对复杂一点儿。

[NOIP2004 普及组] FBI 树队列解法http://t.csdn.cn/ZLgIn

递归做法：

对于上述的队列做法，我们还有一种更优的算法，就是直接递归求解。

我们为什么要先得到层次遍历数组之后再后序遍历呢？为什么题目中让我们直接输出后序遍历呢？

对于一个FBI树，如果要得到后序遍历，我们当然是先处理左节点之后处理右节点，最后处理根节点，这就是后序遍历 而刚好我们构建这颗FBI树的时候不也是递归先处理左子节点，再处理右子节点之后再处理自身吗

那么我们就有了一个思路:

对于一个范围，我们可以处理这个范围的左范围之后处理右范围，而每个范围都是一直进入左范围，到最后不就到了叶节点，处理完叶节点之后会退回上层处理右边的叶节点，再退回去处理他们的父结点，而这刚好就是后序遍历

所以我们可以写出下面的递归代码，只要当前范围不是叶节点，我们就继续进去处理左范围和右范围，一直到l==r的情况，这种情况也就是说我们只需要判断是1还是0输出即可，然后退回去处理右节点。在这之后，程序会退回到父结点，然后继续判断这个范围是F、B还是I

#include<bits/stdc++.h>
using namespace std;
int n;
char t[1050];
void FBI(int l,int r){
    if(l<r){
        FBI(l,(l+r)/2);
        FBI((l+r)/2+1,r);
    }
    bool f1=1,f2=1;
    for(int i=l;i<=r;i++){
        if(t[i]=='1') 
		  f1 = 0;
        else if(t[i]=='0') 
		  f2=0;
    }
    if(!f1&&!f2)
      printf("F");
    else if(f2&&!f1)
      printf("I");
    else if(f1&&!f2)
      printf("B");
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=pow(2,n);i++)
      cin>>t[i];
    FBI(1,pow(2,n));
    return 0;
}