引言

上一节介绍了从反向传播过程的角度认识$\text{LSTM}$如何抑制梯度消失的问题。本节以$\text{LSTM}$的问题为引，介绍它的一种轻量级变体——门控循环单元。

回顾：$\text{LSTM}$的前馈计算过程

关于$\text{LSTM}$的结构展开图与前馈计算过程表示如下：

对应一个单元$(\text{Cell})$的前馈计算过程：
$$\{\begin{array}{l}\begin{array}{rl}& f^{(t)}=\sigma \left[{\mathcal{W}}_{\mathcal{H}\Rightarrow \mathcal{F}}\cdot h^{(t-1)}+{\mathcal{W}}_{\mathcal{X}\Rightarrow \mathcal{F}}\cdot x^{(t)}+b_{\mathcal{F}}\right]\\ & i^{(t)}=\sigma \left[{\mathcal{W}}_{\mathcal{H}\Rightarrow \mathcal{I}}\cdot h^{(t-1)}+{\mathcal{W}}_{\mathcal{X}\Rightarrow \mathcal{I}}\cdot x^{(t)}+b_{\mathcal{I}}\right]\\ & {\tilde{\mathcal{C}}}^{(t)}=\text{Tanh}\left[{\mathcal{W}}_{\mathcal{H}\Rightarrow \tilde{\mathcal{C}}}\cdot h^{(t-1)}+{\mathcal{W}}_{\mathcal{X}\Rightarrow \tilde{\mathcal{C}}}\cdot x^{(t)}+b_{\tilde{\mathcal{C}}}\right]\\ & {\mathcal{C}}^{(t)}=f^{(t)}\ast {\mathcal{C}}^{(t-1)}+i_t\ast {\tilde{\mathcal{C}}}^{(t)}\\ & o^{(t)}=\sigma \left[{\mathcal{W}}_{\mathcal{H}\Rightarrow \mathcal{O}}\cdot h^{(t-1)}+{\mathcal{W}}_{\mathcal{X}\Rightarrow \mathcal{O}}\cdot x^{(t)}+b_{\mathcal{O}}\right]\\ & h^{(t)}=o^{(t)}\ast \text{Tanh}({\mathcal{C}}^{(t)})\end{array}\end{array}$$
对应的权重参数有：
$$\theta =\{\begin{array}{l}{\mathcal{W}}_{\mathcal{H}\Rightarrow \cdot }:{\mathcal{W}}_{\mathcal{H}\Rightarrow \mathcal{F}},{\mathcal{W}}_{\mathcal{H}\Rightarrow \mathcal{I}},{\mathcal{W}}_{\mathcal{H}\Rightarrow \tilde{\mathcal{C}}},{\mathcal{W}}_{\mathcal{H}\Rightarrow \mathcal{O}}\\ {\mathcal{W}}_{\mathcal{X}\Rightarrow \cdot }:{\mathcal{W}}_{\mathcal{X}\Rightarrow \mathcal{F}},{\mathcal{W}}_{\mathcal{X}\Rightarrow \mathcal{I}},{\mathcal{W}}_{\mathcal{X}\Rightarrow \tilde{\mathcal{C}}},{\mathcal{W}}_{\mathcal{X}\Rightarrow \mathcal{O}}\\ b:b_{\mathcal{F}},b_{\mathcal{I}},b_{\mathcal{O}},b_{\tilde{\mathcal{C}}}\end{array}$$

该结构相比于循环神经网络$(\text{Recurrent Neural Network,RNN})$在反向传播过程中，每一个时刻的前项传递过程，对应的参数均会有指数级别的梯度传播路径，并且反向传播过程中各门控结构的输出直接参与反向传播的计算。这种方式有效抑制了梯度消失问题——从梯度累加数量与门控结构的调节角度都可以使各时刻有梯度进行反向传播。

$\text{LSTM}$的问题

虽然$\text{LSTM}$能够抑制梯度消失问题，但需要以增加时间复杂度和空间复杂度作为代价：

• 梯度越向初始时刻方向传播，关于各参数梯度的累加项越多(指数级别增长)，它的梯度计算过程越困难；
• 相比于循环神经网络的权重参数，$\text{LSTM}$需要消耗更多的内存空间存储并更新参数信息。
  这里与$\text{LSTM}$的部分相对应，仅描述‘序列信息传递过程’。
  θ r = { W H ⇒ H , W X ⇒ H , b H } \theta_r = \{\mathcal W_{\mathcal H \Rightarrow \mathcal H},\mathcal W_{\mathcal X \Rightarrow \mathcal H},b_{\mathcal H}\} θr​={WH⇒H​,WX⇒H​,bH​}

并且包含更多类型参数的模型也会更加复杂。从而可能导致过拟合($\text{Overfitting}$)的现象发生。基于此，我们观察门控循环单元$(\text{Gated Recurrent Unit,GRU})$是如何优化该问题的。

$\text{GRU}$的前馈计算过程

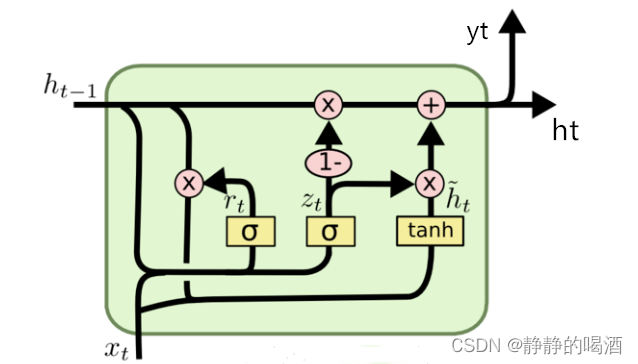
关于$\text{GRU}$的前馈计算过程表示如下：
$$\{\begin{array}{l}\begin{array}{rl}& {\mathcal{Z}}^{(t)}=\sigma \left[{\mathcal{W}}_{\mathcal{H}\Rightarrow \mathcal{Z}}\cdot h^{(t-1)}+{\mathcal{W}}_{\mathcal{X}\Rightarrow \mathcal{Z}}\cdot x^{(t)}+b_{\mathcal{Z}}\right]\\ & r^{(t)}=\sigma \left[{\mathcal{W}}_{\mathcal{H}\Rightarrow r}\cdot h^{(t-1)}+{\mathcal{W}}_{\mathcal{X}\Rightarrow r}\cdot x^{(t)}+b_r\right]\\ & {\tilde{h}}^{(t)}=\text{Tanh}\left[{\mathcal{W}}_{\mathcal{H}\Rightarrow \tilde{\mathcal{H}}}\cdot (r^{(t)}\ast h^{(t-1)})+{\mathcal{W}}_{\mathcal{X}\Rightarrow \tilde{\mathcal{H}}}\cdot x^{(t)}+b_{\tilde{\mathcal{H}}}\right]\\ & h^{(t)}=(1-{\mathcal{Z}}^{(t)})\ast h^{(t-1)}+{\mathcal{Z}}^{(t)}\ast {\tilde{h}}^{(t)}\end{array}\end{array}$$

从结构图与公式角度观察$\text{GRU}$和$\text{LSTM}$之间的差别：

• 相比于$\text{LSTM}$，$\text{GRU}$删除了细胞状态$(\text{Cell State})$，和循环神经网络相同，只有一种序列信息$h^{(t)}(t=1,2,\cdots ,\mathcal{T})$在各时刻之间传递；
• 相比于$\text{LSTM}$，$\text{GRU}$少了一个门控结构，从而减少了一对权重矩阵${\mathcal{W}}_{\mathcal{H}\Rightarrow \cdot },{\mathcal{W}}_{\mathcal{X}\Rightarrow \cdot }$和偏置项$b_{.}$；

其中${\mathcal{Z}}^{(t)}$被称作更新门$(\text{Update Gate})$；$r^{(t)}$被称作重置门$(\text{Reset Gate})$。$\text{LSTM}$和$\text{GRU}$在逻辑上的核心区别有：

• 在$\text{LSTM}$，各门控结构$f^{(t)},i^{(t)},o^{(t)}$与细胞状态${\tilde{\mathcal{C}}}^{(t)}$之间的训练过程相互独立；仅在融合过程中对各神经元的输出分布进行运算：
  上述$4$个隐变量中的输入均是$h^{(t-1)},x^{(t)}$;并且学习过程中，各神经元互不干扰。
  $$\begin{gathered} {\mathcal{C}}^{(t)}=f^{(t)}\ast {\mathcal{C}}^{(t-1)}+i_t\ast {\tilde{\mathcal{C}}}^{(t)} \\ {h}^{(t)}=o^{(t)}\ast \text{Tanh}({\mathcal{C}}^{(t)}) \end{gathered}$$

• 在$\text{GRU}$的细胞单元中，关于当前时刻的候选状态${\tilde{h}}^{(t)}$的训练过程中，其输入就已经被挑选过了：
  $${\tilde{h}}^{(t)}=\text{Tanh}\left[{\mathcal{W}}_{\mathcal{H}\Rightarrow \tilde{\mathcal{H}}}\cdot (r^{(t)}\ast h^{(t-1)})+{\mathcal{W}}_{\mathcal{X}\Rightarrow \tilde{\mathcal{H}}}\cdot x^{(t)}+b_{\tilde{\mathcal{H}}}\right]$$
  很明显，$r^{(t)}\ast h^{(t-1)}$相当于仅将未被遗忘的序列信息进行训练，而$(1-r^{(t)})\ast h^{(t-1)}$就已经被遗忘了。基于这种机制，使得候选状态${\tilde{h}}^{(t)}$的分布结果比${\tilde{\mathcal{C}}}^{(t)}$更有价值(指向性)。逻辑上就没有必要再使用类似输入门结构对其进行约束了。
  一个是对‘输出分布’进行挑选，另一个是在输入分布时进行挑选。

  虽然使用了更精炼的输入分布，但该神经元的作用依然是求解当前时刻候选信息的后验概率分布$\mathcal{P}({\tilde{h}}^{(t)}\mid h^{(t-1)},x^{(t)})$。因此，和$\text{LSTM}$一样，最终输出$h^{(t)}$依然要对$h^{(t-1)}$与${\tilde{h}}^{(t)}$进行重新配比。但是这个配比相比之下简单很多。因为：$h^{(t-1)}$由各时刻的候选状态${\tilde{h}}^{(t)}(t=1,2,\cdots )$组成，而每个时刻求解候选状态${\tilde{h}}^{(t)}$的过程中，均已经将不必要的信息进行遗忘，因而不需要再对$h^{(t-1)}$再执行遗忘：
  $$h^{(t)}=(1-{\mathcal{Z}}^{(t)})\ast h^{(t-1)}+{\mathcal{Z}}^{(t)}\ast {\tilde{h}}^{(t)}$$

  个人理解：
  输入门$i^{(t)}$是遗忘门$f^{(t)}$的对称操作。
  在$\text{LSTM}$中，对于过去时刻的序列信息${\mathcal{C}}^{(t-1)}$和候选信息${\tilde{\mathcal{C}}}^{(t)}$:
  $$\{\begin{array}{l}{\mathcal{C}}^{(t-1)}=f^{(t-1)}\ast {\mathcal{C}}^{(t-2)}+i^{(t-1)}\ast {\tilde{\mathcal{C}}}^{(t-1)}\\ {\tilde{\mathcal{C}}}^{(t)}=\text{Tanh}\left[{\mathcal{W}}_{h^{(t-1)}\Rightarrow {\tilde{\mathcal{C}}}^{(t)}}\cdot h^{(t-1)}+{\mathcal{W}}_{x^{(t)}\Rightarrow {\tilde{\mathcal{C}}}^{(t)}}\cdot x^{(t)}+b_{\tilde{\mathcal{C}}}\right]\end{array}$$
  它们的输入均是 h ( τ ) , x ( τ ) ( τ ∈ { 1 , 2 , ⋯ T } ) h^{(\tau)},x^{(\tau)}(\tau \in \{1,2,\cdots \mathcal T\}) h(τ),x(τ)(τ∈{1,2,⋯T})，因而在计算对应后验概率分布的过程中，它们到底使用哪些信息作为条件，我们是不可探究的；
  其中$x^{(\tau )}$是输入特征，不作考虑;但$h^{(\tau )}$作为序列信息，在表示${\mathcal{C}}^{(t-1)}.{\tilde{\mathcal{C}}}^{(t)}$后验的各神经元之间无交集，各自使用哪些‘过去信息’进行学习，未知，都有可能;
  
  但$\text{GRU}$中，$h^{(t-1)},{\tilde{h}}^{(t)}$的输入均是被挑选(未被遗忘)的优质信息，导致它们的后验分布相比于之前的不可探究，更有指向性。因此，遗忘门和输入门这一对相辅相成的门控结构都被省略掉了。
  
  而${\mathcal{Z}}^{(t)}$不是输入门，它仅仅是在$\text{Sigmoid}$激活函数的值域$(0,1)$下，权衡$h^{(t-1)}$与${\tilde{h}}^{(t)}$之间比例关系的一个比率系数而已。

  其中${\mathcal{Z}}^{(t)}$仅表示学习出的一个比例系数；而$1-{\mathcal{Z}}^{(t)}$是基于$\text{Sigmoid}$激活函数的值域描述的${\mathcal{Z}}^{(t)}$之外剩下的比例结果。将$h^{(t-1)}$与${\tilde{h}}^{(t)}$之间的比例进行调整，并将最终的和作为输出。

$\text{GRU}$的优势

首先，$\text{GRU}$的参数更少，从而有效降低过拟合的风险；并且在反向传播的过程中，随着反向传播深度的加深，对应需要反向传播路径相比于$\text{LSTM}$大量减少。从而减小了时间、空间复杂度的负担。