（1）概念

点积在数学中，又称数量积（dot product; scalar product），是指接受在实数R上的两个向量并返回一个实数值标量的二元运算。

两个向量a = [a1, a2,…, an]和b = [b1, b2,…, bn]的点积定义为：

a·b=a1b1+a2b2+……+anbn。

使用矩阵乘法并把（纵列）向量当作n×1 矩阵，点积还可以写为：

a·b=（a^T）*b，这里的a^T指示矩阵a的转置。

（2）机器学习中几种常见的乘积(product)

参考：(1条消息) 机器学习中几种常见的乘积(product)_oldlybaby的博客-CSDN博客_frobenius内积

一、Frobenius inner product （矩阵内积）
适用范围：两个相同大小的矩阵
符号表示：< A , B > F
定义：给定两个大小均为m × n m \times nm×n的实矩阵A , B \mathbf{A},\mathbf{B}A,B，即：

二、dot product (点积)
注：矩阵内积退化成向量形式就是点积，也可以称作向量内积

适用范围：维度相同的两个向量
符号表示：a ⋅ b 
定义：
对于两向量 a=[a1, ... ,an]和b = [ b 1 ,   . . .   , b n ]

---

---

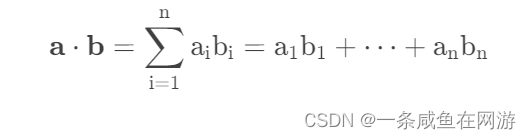
持续学习！！！