1、几何矩和Hu矩

1.1几何矩

a）几何计算公式：

        

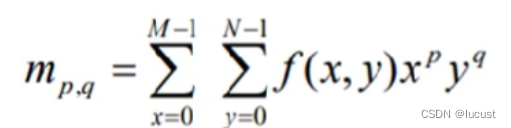
        p、q为阶数，当p+q = 1时，几何矩为一阶矩，p+q = 2，几何矩为二阶矩，依次类推。。

因此，对于二值图像有：

        所有前景像素的x坐标之和：

        所有前景像素的y坐标之和：

        所有前景像素的个数：

        注：前景像素为像素值为对应类型的满像素值的像素。

b）几何中心矩计算公式

        

         

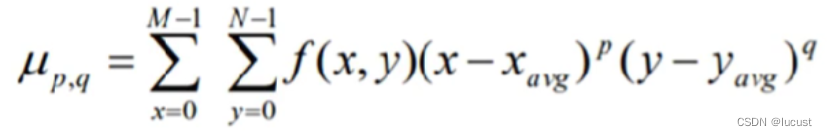
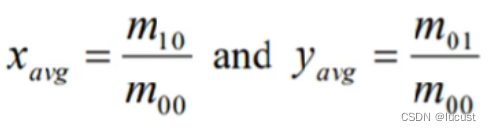
1.2 Hu矩

Hu矩计算公式：

        

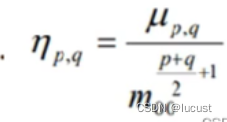
         性质：Hu矩具有放缩不变性，旋转不变性。

        利用下述7个值来进行轮廓匹配：

        

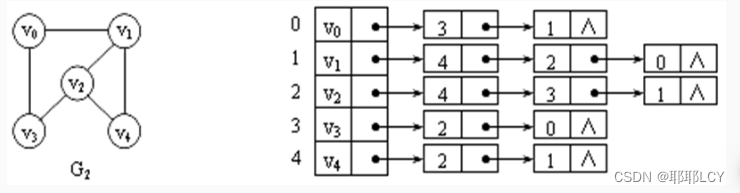
 2、基于Hu矩的轮廓匹配

        两个轮廓的参数计算公式（这里的即为上面的值）。

        

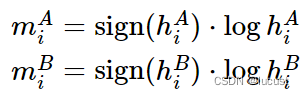
        两个轮廓的相似度计算公式： 

        

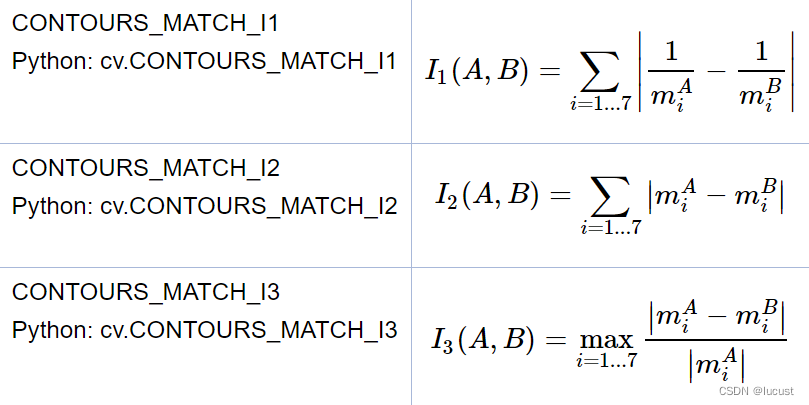
         在常规使用时，常预设一个阈值，将相似度值与阈值进行比较，设定相似度大于阈值的两个轮廓为同一轮廓。

3、代码

步骤：
    1、任选图像2中的一个轮廓，计算其Hu矩
    2、对图像1所有轮廓计算Hu矩，将图像2的Hu矩与图像1的所有Hu进行比较
    3、相似度阈值操作。

void QuickDemo::contour_get(Mat& image, vector<vector<Point>>& contours)
{
	//高斯模糊
	Mat dst;
	GaussianBlur(image, dst, Size(3, 3), 0);
	Mat gray;
	cvtColor(dst, gray, COLOR_BGR2GRAY);

	Mat binary;
	threshold(gray, binary, 0, 255, THRESH_BINARY_INV | THRESH_OTSU);
	/*namedWindow("THRESH_OTSU", WINDOW_FREERATIO);
	imshow("THRESH_OTSU", binary);*/
	//查找轮廓
	vector<Vec4i> hierachy;
	findContours(binary, contours, hierachy, RETR_EXTERNAL, CHAIN_APPROX_SIMPLE, Point());
	cout << contours.size() << endl;
}
void QuickDemo::contour_match(Mat& image1, Mat&image2)
{
	vector<vector<Point>> contours1;
	vector<vector<Point>> contours2;
	contour_get(image1, contours1);
	contour_get(image2, contours2);

	/*
	* 步骤：
	* 1、任选图像2中的一个轮廓，计算其Hu矩
	* 2、对图像1所有轮廓计算Hu矩，将图像2的Hu矩与图像1的所有Hu进行比较
	* 3、相似度阈值操作。
	*/
	//Hu矩计算
	Moments mm2 = moments(contours2[0]);//先计算几何矩
	Mat hu2;
	HuMoments(mm2, hu2);
	for (size_t t = 0; t < contours1.size(); ++t) {
		Moments mm = moments(contours1[t]);//先计算几何矩
		Mat hu;
		HuMoments(mm, hu);
		double sim_value = matchShapes(hu, hu2, CONTOURS_MATCH_I1, 0);
		//在原图绘制相似轮廓
		if (sim_value < 1) {
			cout << "第" << t << "个轮廓的相似度值为：" << (float)(1 - sim_value) << endl;
			drawContours(image1, contours1, t, Scalar(0, 255, 0), 2, 8);
			drawContours(image2, contours2, 0, Scalar(0, 255, 0), 2, 8);
		}
		
		//获取图像1轮廓的中心位置
		double cx = mm.m10 / mm.m00;
		double cy = mm.m01 / mm.m00;
		circle(image1, Point(cx, cy), 2, Scalar(255, 0, 0), 2, 8);//在中心位置画圆
	}
	namedWindow("contours1", WINDOW_FREERATIO);
	imshow("contours1", image1);
	namedWindow("image2", WINDOW_FREERATIO);
	imshow("image2", image2);
}

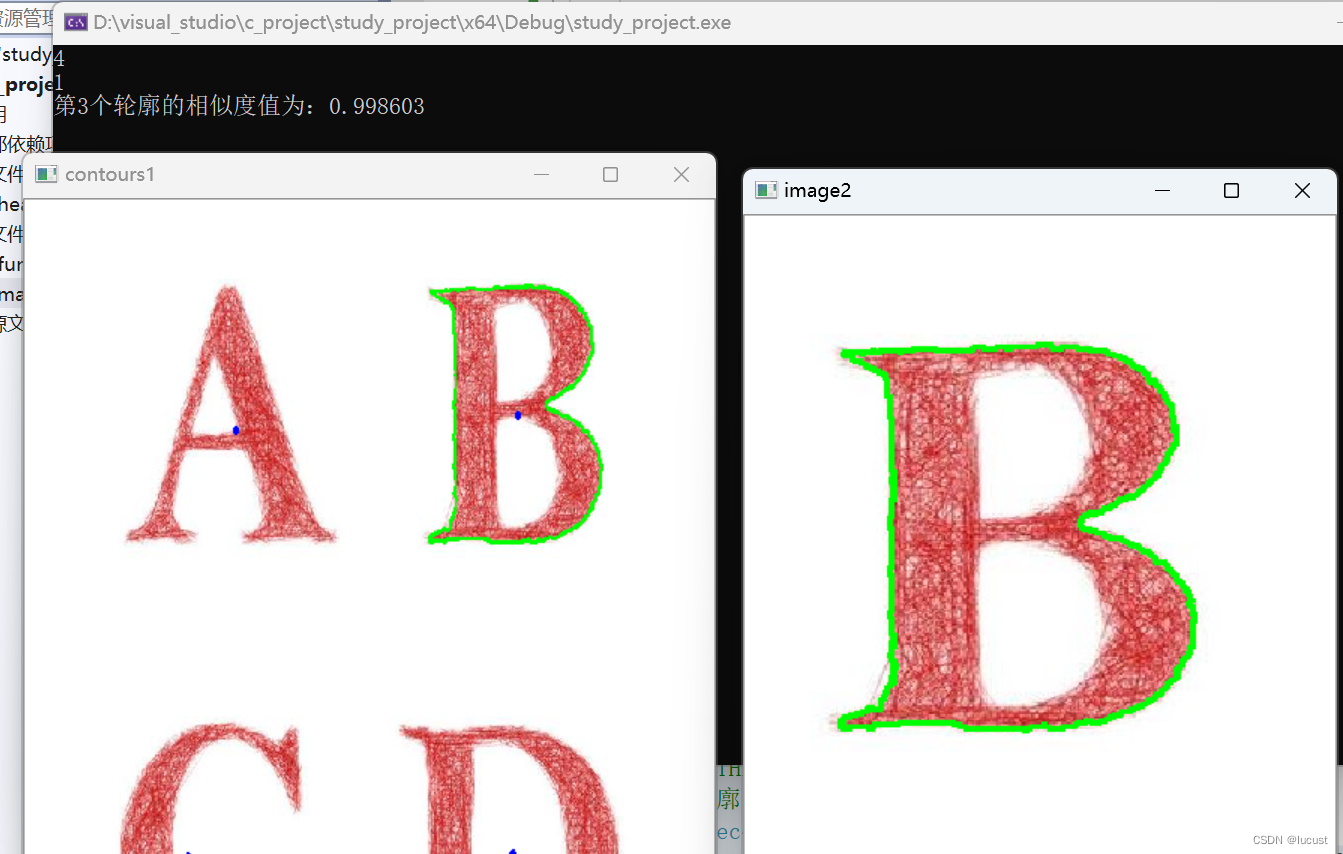
 结果：