分析理论是统计学和数据分析中的重要概念，它们用于描述和理解数据的集中趋势、离中趋势、数据分布以及抽样理论。下面是对这些概念的简要说明：

• 集中趋势： 均值、中位数与分位数、众数
• 离中趋势：标准差、方差
• 数据分布：偏态与峰态、正态分布与三大分布
• 抽样理论：抽样误差、抽样精度 请对上述的概念进行简要的说明，并提供对应示例以及公式

1 集中趋势

1.1 概述

集中趋势是描述数据分布中心位置的统计概念，用于了解数据的典型取值或平均水平。主要包括均值、中位数和众数。

1.2 理论

（1）均值（Mean）：均值是指将所有数据值相加后除以数据的总个数，用于表示数据的平均水平。均值对于正态分布的数据是一个有意义的衡量指标。计算公式如下：

均值 = (数据值1 + 数据值2 + ... + 数据值n) / n

例如1，对于数据集 [3, 5, 7, 9, 11]，均值为 (3 + 5 + 7 + 9 + 11) / 5 = 7。

例如2，计算一组数据的平均年龄，即将所有年龄值相加并除以数据点的个数。

（2）中位数（Median）：中位数是指将数据按照大小排序后位于中间位置的值。对于有奇数个数据的集合，中位数是排序后的中间值；对于有偶数个数据的集合，中位数是中间两个值的平均值。中位数对于存在极端值或偏态数据的情况更具鲁棒性。计算中位数的方法如下：

• 对于奇数个数据，中位数是排序后的中间值。
• 对于偶数个数据，中位数是排序后的中间两个值的平均值。

例如，找出一组学生考试成绩的中位数，将成绩按升序排列，找出中间位置的值。

（3）分位数（Quantiles）：将一组数据按升序排列，然后分割成等分的点，如四分位数（Quartiles）将数据分为四个等分点，用于描述数据的分布情况。

例如，找出一组学生考试成绩的中位数，将成绩按升序排列，找出中间位置的值。

（4）众数（Mode）：众数是指数据集中出现次数最频繁的值。一个数据集可以有一个或多个众数，或者没有众数。众数对于描述离散型数据的集中趋势很有用。

例如，对于数据集 [3, 5, 7, 5, 9, 5, 11]，众数为 5。

1.3 四分位数示例

给定以下一组数据：1, 2, 3, 4, 5, 6, 7, 8, 9

我们可以按照四分位数的计算方法计算出相应的值：

（1）. 首先，根据数据的个数确定位置：
   n = 9

（2）. 计算Q1的位置：
   Q1的位置 = (n + 1) * 0.25
                    = 10 * 0.25
                    = 2.5

   Q1的位置是一个小数，表示在排序后的数据中的位置，这意味着Q1将位于第2和第3个数据之间。

（3）. 计算Q2的位置（中位数）：
   Q2的位置 = (n + 1) * 0.5
            = 10 * 0.5
            = 5

   Q2的位置是一个整数，表示在排序后的数据中的位置，这意味着Q2将位于第5个数据上。

（4）. 计算Q3的位置：
   Q3的位置 = (n + 1) * 0.75
            = 10 * 0.75
            = 7.5

   Q3的位置是一个小数，表示在排序后的数据中的位置，这意味着Q3将位于第7和第8个数据之间。

（5）. 计算四分位数的值：
   Q1的值 = 数据排序后的第2个数据 + (Q1的位置的小数部分 * (数据排序后的第3个数据 - 数据排序后的第2个数据))
   Q2的值 = 数据排序后的第5个数据
   Q3的值 = 数据排序后的第7个数据 + (Q3的位置的小数部分 * (数据排序后的第8个数据 - 数据排序后的第7个数据))

将数据排序后为：1, 2, 3, 4, 5, 6, 7, 8, 9

根据上述计算方法，我们可以得到：
Q1 = 2 + (0.5 * (3 - 2)) = 2.5
Q2 = 5
Q3 = 7 + (0.5 * (8 - 7)) = 7.5

因此，给定的数据集的四分位数为：
Q1 = 2.5
Q2 = 5
Q3 = 7.5

2. 离中趋势

2.1 概述

离中趋势是描述数据分布中数据离开中心位置的程度或变异程度的统计概念。主要包括标准差和方差。

2.2 理论

（1）标准差（Standard Deviation）：标准差是方差的平方根，表示数据与均值之间的差异的平均值的平方根。标准差是衡量数据集离散程度的常用指标，它的数值具有与原始数据相同的度量单位，因此更直观地反映了数据的变异程度。计算公式如下：

标准差 = 方差的平方根

例如，对于数据集 [3, 5, 7, 9, 11]，标准差为 √8 ≈ 2.83。

例如，计算一组学生的考试成绩的标准差，用于衡量成绩的离散程度。

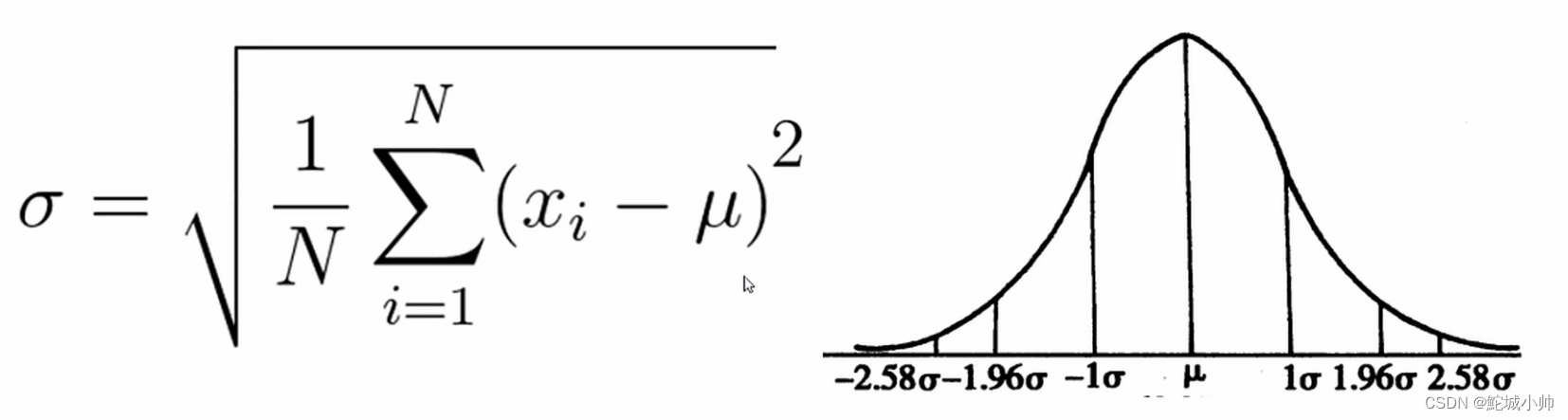
 （2）方差（Variance）：标准差的平方，描述数据的离散程度。方差是指数据与其均值之间差异的平方的平均值。方差衡量了数据集的离散程度，数值越大表示数据的离散程度越大，数值越小表示数据的离散程度越小。计算公式如下：

方差 = [(数据值1 - 均值)^2 + (数据值2 - 均值)^2 + ... + (数据值n - 均值)^2] / n

例如1，对于数据集 [3, 5, 7, 9, 11]，均值为 7，计算方差为 [(3 - 7)^2 + (5 - 7)^2 + (7 - 7)^2 + (9 - 7)^2 + (11 - 7)^2] / 5 = 8。

例如2，计算一组学生的考试成绩的标准差，用于衡量成绩的离散程度。

3. 数据分布

3.1 概述

数据分布是指数据在数值上的分布情况，描述了数据在不同取值上的频率或概率分布。数据分布的概述包括了偏态与峰态的概念以及常见的分布类型如正态分布和三大分布。

3.2 理论

（1） 偏态（Skewness）与峰态（Kurtosis）：用于描述数据分布的形状特征。偏态度量数据分布的不对称程度，正态分布的偏态为0；峰态度量数据分布的尖峰或扁平程度，正态分布的峰态为3。

例如1，分析一组股票收益率数据的偏态和峰态，来了解数据分布的形状特征。

偏态示例： 假设有一个数据集 [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]，它是一个对称分布，没有偏态。偏态系数为0。

峰态示例：假设有两个数据集：数据集A [1, 1, 1, 1, 1] 和数据集B [1, 2, 3, 8, 9]。数据集A是一个平坦分布，数据集B是一个尖峰分布。对于数据集A，峰态系数接近3，而对于数据集B，峰态系数大于3。

相关公式：

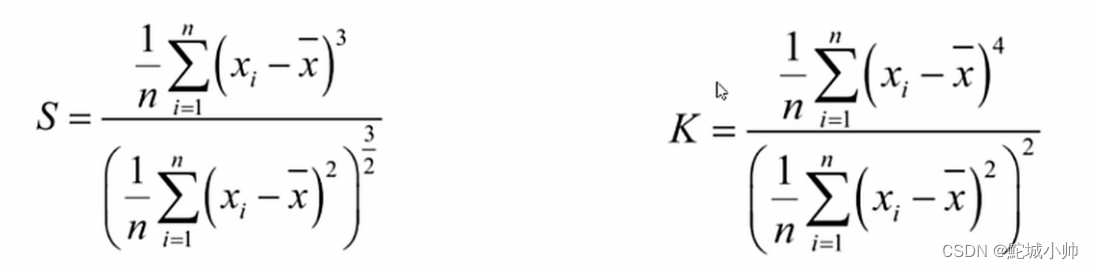
（2）正态分布与三大分布：正态分布是统计学中常见的连续概率分布，具有对称的钟形曲线。三大分布指正态分布、均匀分布和指数分布，它们在统计学和数据分析中经常被使用。

例如，分析一组股票收益率数据的偏态和峰态，来了解数据分布的形状特征。

正态分布：

公式：

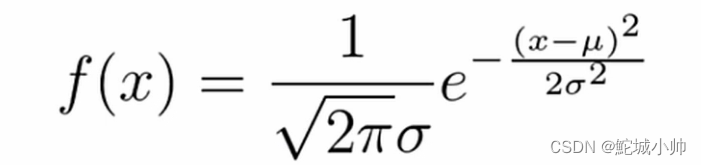
卡方分布:

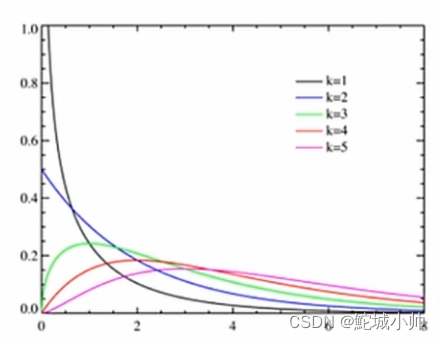
t分布:

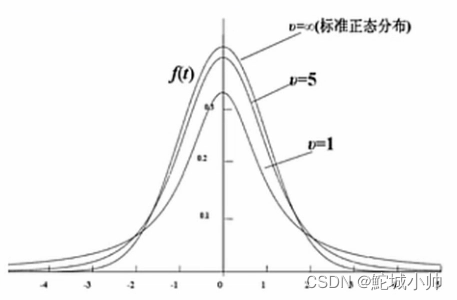
f分布：

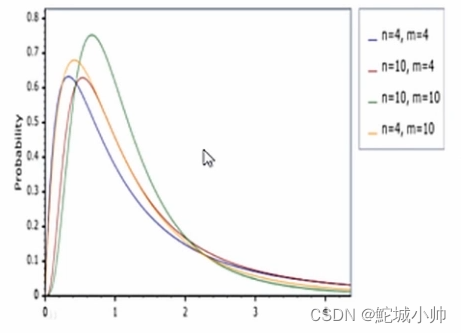
4 抽样理论：

4.1 概述

抽样理论是统计学中的重要概念，用于研究如何从总体中获取样本，并通过样本推断总体的特征。

4.2 理论

（1）抽样误差（Sampling Error）：在从总体中抽取样本进行统计推断时，样本与总体之间的差异引起的误差。抽样误差的大小取决于样本的大小和抽样方法的质量。

例如，从整个人口中随机抽取一部分样本进行调查，样本结果可能与整个人口存在一定的差异，这是抽样误差。

（2）抽样精度（Sampling Precision）：衡量样本估计值与总体真值之间的接近程度。较小的抽样误差和较高的抽样精度表示样本估计值较接近总体真值。

例如，通过增加样本容量或改进抽样方法，减小抽样误差，提高抽样精度，使样本结果更加接近总体特征。

这些分析理论和概念在数据分析和统计推断中具有重要意义，帮助我们理解数据的特征、分布和误差。

4.3 抽样误差与精度

4.3.1 抽样平均误差计算公式：

（1）重复抽样：

• μx² 表示样本平均值的平方
• σ² 表示总体方差
• n 表示样本的大小

根据这个公式，通过样本平均值的平方乘以样本大小来估计总体方差。该公式的推导基于总体方差的性质以及样本均值的性质。

需要注意的是，这个公式是一个无偏估计量，即在样本足够大的情况下，样本平均值的平方除以样本大小可以无偏估计总体方差。然而，对于小样本情况下的方差估计，可能存在一定的偏差。

 （2）不重复抽样：

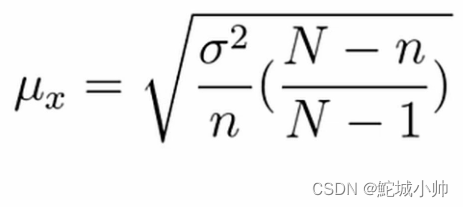
• μx² 表示校正后的样本方差
• σ² 表示总体方差
• n 表示样本大小
• N 表示总体大小

根据这个公式，通过将样本方差除以 n，并乘以校正因子 ( (N - n)/ (N-1) )，可以得到更接近总体方差的估计。

这个校正因子考虑了样本的大小和总体的大小之间的比例关系，通过调整样本方差的估计，使其更准确地反映总体方差。

需要注意的是，这个公式适用于从一个大总体中抽取相对较小样本的情况，通过校正样本方差，可以更好地估计总体方差。

在实际应用中，如果总体大小 N 远大于样本大小 n，并且需要估计总体方差时，可以使用这个校正公式来得到更准确的估计结果。然而，如果总体大小与样本大小相近或样本很大时，校正因子的影响可能不太明显，可以直接使用样本方差作为总体方差的估计。

4.3.2 估计总体时抽样数目的确定：

重复抽样：

不重复抽样：

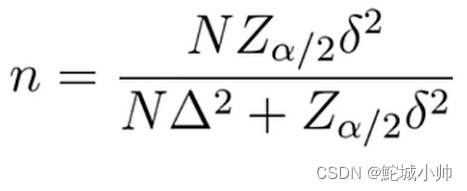
4.4 抽样示例一

示例1： 某鱼塘进行抽样调查，从鱼塘不同部位共网到150条鱼，草鱼123条，草鱼平均2公斤，标准差0.75公斤，95.45概率保证，估计草鱼平均每条的重量。（由于是不同位置，可看做重复抽样）

这里使用 μx=√(σ²/n) 公式：

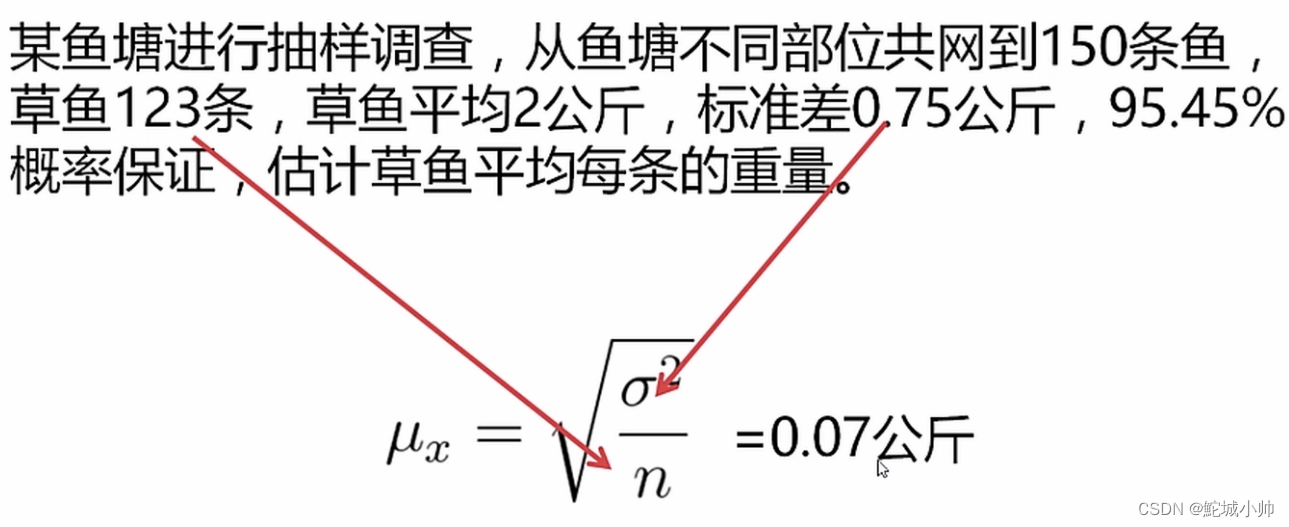
根据给定的信息：

• 样本大小 n = 123 条草鱼
• 草鱼平均重量 μ = 2 公斤
• 草鱼的标准差 σ = 0.75 公斤

我们可以代入这些值到公式中计算每条草鱼每条的平均重量的抽样误差：

μx = √(σ²/n) = √((0.75²) / 123) = √(0.004734) ≈ 0.0688 公斤 = 0.07 公斤

根据概率为95.45%，我们可以使用95%的置信水平，这对应于标准正态分布的临界值。

在标准正态分布中，95%的置信水平对应于标准差的1.96倍。而在这个问题中，我们的均值为2，标准差为0.07。

因此，草鱼重量的范围可以计算为：

下限 = 均值 - (标准差 * 1.96) 上限 = 均值 + (标准差 * 1.96)

下限 = 2 - (0.07 * 1.96) ≈ 1.8672 kg 上限 = 2 + (0.07 * 1.96) ≈ 2.1328 kg

因此，根据给定的概率和标准正态分布的性质，在95.45%的概率下，草鱼的重量范围为约1.8672 kg到约2.1328 kg。请注意，这是一个近似的范围估计，并基于标准正态分布的假设。在实际情况中，可能存在其他因素和不确定性。

5. 使用pandas与scipy分析

深入理解pandas

深入理解scipy

5.1 pandas

• 均值： mean()
• 中位数： median()
• 分位数： quantile(q=0.25)…
• 众数：mode()
• 标准差： .std()
• 方差： var()
• 求和 sum()
• 偏态系数： skew()
• 峰态系数：kurt()

# 引入pandas
import pandas as pd

# 读取数据
df=pd.read_csv("data/HR.csv")

# 查看数据结构类型
type[df]
Out[5]: 
type[       satisfaction_level  last_evaluation  ...  department  salary
0                    0.38             0.53  ...       sales     low
1                    0.80             0.86  ...       sales  medium
2                    0.11             0.88  ...       sales  medium
3                    0.72             0.87  ...       sales     low
4                    0.37             0.52  ...       sales     low
                   ...              ...  ...         ...     ...
14997                0.11             0.96  ...     support     low
14998                0.37             0.52  ...     support     low
14999                 NaN             0.52  ...     support     low
15000                 NaN        999999.00  ...        sale     low
15001                0.70             0.40  ...        sale     nme
[15002 rows x 10 columns]]

# 求均值
df['satisfaction_level'].mean()
Out[6]: 0.6128393333333333

# 求中位数
df['satisfaction_level'].median()
Out[7]: 0.64

# 求分位数
df['satisfaction_level'].quantile(q=0.25)
Out[9]: 0.44

# 求众数
df['satisfaction_level'].mode()
Out[10]: 
0    0.1
Name: satisfaction_level, dtype: float64

# 求标准差
df['satisfaction_level'].std()
Out[11]: 0.24862338135944925

# 求方差
df['satisfaction_level'].var()
Out[12]: 0.061813585758606134

# 求和
df['satisfaction_level'].sum()
Out[13]: 9192.59

# 求偏态系数
df['satisfaction_level'].skew()
Out[14]: -0.47643761717258093

# 求峰态系数
df['satisfaction_level'].kurt()
Out[15]: -0.6706959323886252

5.2 scipy

import scipy.stats as ss

ss.norm   # 生成一个是正态分布
Out[4]: <scipy.stats._continuous_distns.norm_gen at 0x1333b1f4f90>

ss.norm.stats(moments='mvsk')
Out[6]: (0.0, 1.0, 0.0, 0.0)
# mvsk 
# m mean
# v  var
# s skew
# k kurt

ss.norm.pdf(0.0)  # pdf 是输入横坐标，输出纵坐标
Out[8]: 0.3989422804014327

ss.norm.ppf(0.9)  # ppf 是一个累积值，从负无穷大到某点积分是0.9的时候是多少。负无穷到正无穷是1，当时0.9的时候，是多少
Out[10]: 1.2815515655446004

ss.norm.cdf(2)   # 从负无穷到2,它的累积概率是多少
Out[12]: 0.9772498680518208

ss.norm.cdf(2) -ss.norm.cdf(-2) # 0.95
Out[17]: 0.9544997361036416 

ss.norm.rvs(size=10)# 得到10个符合正太分布的数字
Out[19]: 
array([ 1.35927484, -2.27234151, -0.53627446, -0.6049967 ,  1.04646856,
       -0.08009615, -2.12884619,  0.05694344, -0.90168575, -1.07511186])

ss.chi2  # 卡方分布
Out[21]: <scipy.stats._continuous_distns.chi2_gen at 0x13314b53790>

ss.t    # t分布 
Out[21]: <scipy.stats._continuous_distns.t_gen at 0x13361be9550>
 
ss.f  # f 分布
Out[22]: <scipy.stats._continuous_distns.f_gen at 0x13361b87e50>

（1）ss.norm: 生成一个正态分布（正态分布的概率密度函数）的对象，可以用来进行正态分布相关的计算和操作。

（2）ss.norm.stats(moments='mvsk'): 计算正态分布的统计量，包括均值（mean）、方差（variance）、偏度（skewness）和峰度（kurtosis）。

（3）ss.norm.pdf(0.0): 计算正态分布在给定横坐标（0.0）处的概率密度值（即概率密度函数值）。

（4）ss.norm.ppf(0.9): 计算正态分布累积分布函数的逆函数，即给定累积概率（0.9），返回对应的横坐标值。

（5）ss.norm.cdf(2): 计算正态分布累积分布函数的值，即从负无穷大积分到给定横坐标（2）的累积概率。

（6）ss.norm.cdf(2) - ss.norm.cdf(-2): 计算正态分布在给定区间（从-2到2）内的累积概率。

（7）ss.norm.rvs(size=10): 生成符合正态分布的随机变量，返回指定数量（10个）的随机样本。

（8）ss.chi2: 卡方分布对象，用于进行卡方分布相关的计算。

（9）ss.t: t分布对象，用于进行t分布相关的计算。

（10）ss.f: F分布对象，用于进行F分布相关的计算。