适应性哈夫曼编码

简介

适应性哈夫曼编码（Adaptive Huffman coding），又称动态哈夫曼编码（Dynamic Huffman coding），是基于哈夫曼编码的适自适应编码技术。它允许在符号正在传输时构建代码，允许一次编码并适应数据中变化的条件，即随着数据流的到达，动态地收集和更新符号的概率（频率）。一遍扫描的好处是使得源程序可以实时编码，但由于单个丢失会损坏整个代码，因此它对传输错误更加敏感。
在哈夫曼编码中，有个缺点是除了压缩后的资料外，它还得传送机率表给解码端，否则解码端无法正确地做解码的工作。如果想要压缩好一点，必须有更多的统计资料，但同时必须要送出更多的统计资料到解压缩端。而适应性编码可以利用已经读过的资料机动的调整哈夫曼树。适应性哈夫曼编码中，算法FGK的基本原则是根据兄弟性质（Sibling Property），由Gallager定义。一颗哈夫曼树只是一棵在每个节点，包括树叶与内节点，加上加权值得二叉树，除了树根外，每一个节点都有一个兄弟节点与其共有一个父亲节点。如果每一个节点可以按照加权值从小排列到大且每个节点又再自己的兄弟相邻，称为兄弟性质。修改、或更新一棵哈夫曼树包括两个步骤。第一个步骤是频率次数的增加，先找到该叶子，把频率加一，在往上找他的父亲节点，也跟着加一，直到树根皆照着此步骤。第二个步骤是如果增加加权值的动作使得兄弟性质不再满足时，必须做调整的动作，借由交换叶子改变频率增加的顺序，同时，交换位置后的父亲节点加权值也要跟着更新，以此原则使之再度成为哈夫曼树。

算法

自定义哈夫曼编码，预先不知道各种符号的出现频率，编码树的初始状态只包含一个叶节点，即NYT（Not Yet Transmitted），NYT是一个逸出码，不同于任何一个将要传送的符号，当一个尚未包含在编码树中的符号需要被编码时，首先输出NYT的编码，然后跟着符号的原始表达。当解码器解出一个NYT之后，它就知道下面的内容暂时不再是Huffman编码，而是一个从未在编码数据流中出现过的原始符号。当插入一个符号q时，会出现两种情况：

1. q是第一次出现的字符结点。构造一个新的子树，子树包含NYT符号和新符号两个叶节点，如下图所示。然后判断该子树的父节点是否是是当前权重下编号最大的结点，如果是，直接更新权重即可；否则，将父节点与相同权重的编号最高的结点交换，再更新权重值。

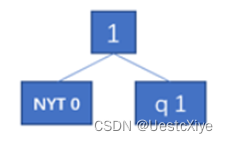
2. q不是第一次出现的字符结点。如果q所在节点，是当前节点权重下编号最大的结点，则直接使其当前节点权重及父节点权重加1即可。否则，将当前节点与相同权重的编号最高的结点交换，再更新权重值。

示例

以字符串“aabbbacc”的编码和解码为例，假设原始共有四类字符（a,b,c,d）,规定初始化编码：a-00，b-01，c-10，d-11，此为编码器与解码器双方的约定。

编码过程：

1. 初始状态，仅有NYT节点，权重为0。
   

2. 输入字符a，为新字符，输出编码000。0为NYT编码，00是a的初始编码，此时的huffman树为：
   

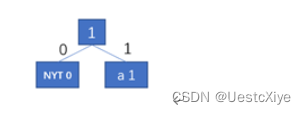
3. 输入字符a，输出编码1。将a加入到huffman树中，并进行调整。
   

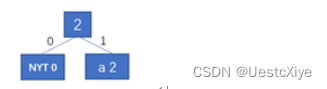
4. 输入字符b，为新字符，输出编码001。0是NYT编码，01是b的初始编码。
   

5. 输入字符b,输出编码01。将字符b加入到huffman树中，并进行调整。
   

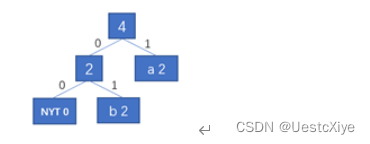
6. 输入字符b，输出编码01。将字符b加入到huffman树中，注意此时b节点不是当前权重值下编号最大的节点，需要进行节点的交换操作，即节点（2）与节点（4）交换。
   

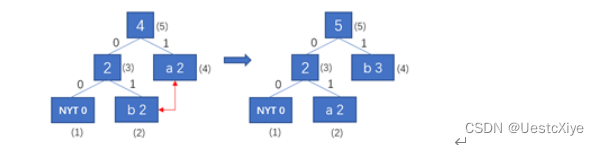
7. 输入字符a,输出编码01，将a加入到huffman树中。
   

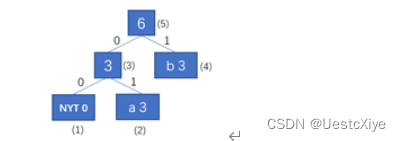
8. 输入字符c，为新字符，输入编码0010。00是NYT编码，10是c的初始编码。该子树的父节点（5）不是当前权重下编号最大的节点，所以节点（5）与节点（6）交换，并更新权重值。
   

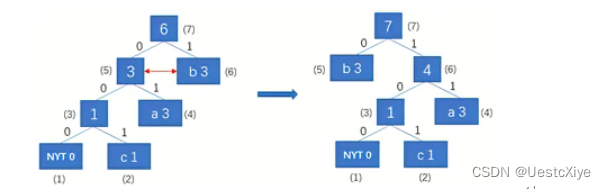
9. 输入字符c，输出编码101，将字符c加入到huffman树中。
   

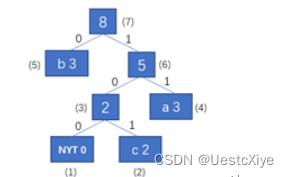
综上所述，字符串“aabbbacc”动态哈夫曼编码的结果为00010010101010010101。

解码过程：

由于自适应Huffman编码算法采用了先编码，后调整编码树的方案，相应的解码算法比较简单。解码算法也使用仅有唯一的NYT节点的编码树作为初始状态，然后根据Huffman编码数据流，对符号进行还原。每次处理完一个符号，就使用这个符号调整编码树。这样，在每一次输入新的符号之前，Huffman树都处于与进行编码时使用的Huffman树完全相同的状态,保证了解码的正确性。