0 专栏介绍

🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备！详细介绍全局规划(图搜索、采样法、智能算法等)；局部规划(DWA、APF等)；曲线优化(贝塞尔曲线、B样条曲线等)。

🚀详情：图解自动驾驶中的运动规划(Motion Planning)，附几十种规划算法

1 图解RRT*算法原理

RRT*算法针对传统RRT算法进行了渐进最优改进，在添加 $x_{\mathrm{new}}$ 到搜索树的过程中进行重连选择(Rewire)：构造以 $x_{\mathrm{new}}$ 为圆心 $r$ 为优化半径的邻域圆，找到与 $x_{\mathrm{new}}$ 连接后路径代价最小的点 $x_{\mathrm{min}}$ 作为 $x_{\mathrm{new}}$ 的父节点，而非直接将 $x_{\mathrm{near}}$ 、 $x_{\mathrm{new}}$ 相连；与此同时也会优化圆内其他节点 $x_n$ 的代价——若路径

$\left< x_{\mathrm{init}},\cdots ,x_{\mathrm{n}} \right> >\left< x_{\mathrm{init}},\cdots ,x_{\mathrm{new}},x_{\mathrm{n}} \right>$

则将 $x_{\mathrm{new}}$ 重连为 $x_n$ 的父节点，如图所示。

在这里插入图片描述

RRT*算法流程如下所示，与RRT算法相比只是增加了一个重连优化函数，更新节点连接情况

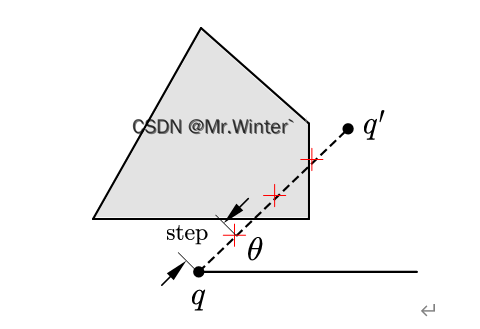
在这里插入图片描述

其中碰撞检测算法 $\mathrm{CollisionFree}\left( \cdot \right)$ 常用连线采样法，如图所示，计算概率路图中的连线 $\left( q,q' \right)$ 是否合法需要考虑两个方面

连线长度小于阈值 $\mathrm{d}\left( q,q' \right) <\mathrm{d}_{\max}$ ， $\mathrm{d}_{\max}$ 对无意义的长距离连线进行剪枝；
连线不穿过障碍：在连线上按一定步长采样，判断是否存在落入障碍中的采样点。

在这里插入图片描述

2 ROS C++算法实现

核心代码如下所示

Node RRTStar::_findNearestPoint(std::unordered_set<Node, NodeIdAsHash, compare_coordinates> list, Node& node)
{
  Node nearest_node, new_node(node);
  double min_dist = std::numeric_limits<double>::max();

  for (const auto node_ : list)
  {
    // calculate distance
    double new_dist = _dist(node_, new_node);

    // update nearest node
    if (new_dist < min_dist)
    {
      nearest_node = node_;
      new_node.pid_ = nearest_node.id_;
      new_node.g_ = new_dist + node_.g_;
      min_dist = new_dist;
    }
  }

  // distance longer than the threshold
  if (min_dist > max_dist_)
  {
    // connect sample node and nearest node, then move the nearest node
    // forward to sample node with `max_distance` as result
    double theta = _angle(nearest_node, new_node);
    new_node.x_ = nearest_node.x_ + (int)(max_dist_ * cos(theta));
    new_node.y_ = nearest_node.y_ + (int)(max_dist_ * sin(theta));
    new_node.id_ = grid2Index(new_node.x_, new_node.y_);
    new_node.g_ = max_dist_ + nearest_node.g_;
  }

  // obstacle check
  if (!_isAnyObstacleInPath(new_node, nearest_node))
  {
    // rewire optimization
    for (auto node_ : sample_list_)
    {
      // inside the optimization circle
      double new_dist = _dist(node_, new_node);
      if (new_dist < r_)
      {
        double cost = node_.g_ + new_dist;
        // update new sample node's cost and parent
        if (new_node.g_ > cost)
        {
          if (!_isAnyObstacleInPath(new_node, node_))
          {
            new_node.pid_ = node_.id_;
            new_node.g_ = cost;
          }
        }
        else
        {
          // update nodes' cost inside the radius
          cost = new_node.g_ + new_dist;
          if (cost < node_.g_)
          {
            if (!_isAnyObstacleInPath(new_node, node_))
            {
              node_.pid_ = new_node.id_;
              node_.g_ = cost;
            }
          }
        }
      }
      else
        continue;
    }
  }
  else
    new_node.id_ = -1;
  return new_node;
}

在这里插入图片描述

3 Python算法实现

核心代码如下

def getNearest(self, node_list: list, node: Node) -> Node:
	'''
	Get the node from `node_list` that is nearest to `node` with optimization.
	
	Parameters
	----------
	node_list: list
	    exploring list
	node: Node
	    currently generated node
	
	Return
	----------
	node: Node
	    nearest node 
	'''
	node_new = super().getNearest(node_list, node)
	if node_new:
	    #  rewire optimization
	    for node_n in node_list:
	        #  inside the optimization circle
	        new_dist = self.dist(node_n, node_new)
	        if new_dist < self.r:
	            cost = node_n.g + new_dist
	            #  update new sample node's cost and parent
	            if node_new.g > cost and not self.isCollision(node_n, node_new):
	                node_new.parent = node_n.current
	                node_new.g = cost
	            else:
	                #  update nodes' cost inside the radius
	                cost = node_new.g + new_dist
	                if node_n.g > cost and not self.isCollision(node_n, node_new):
	                    node_n.parent = node_new.current
	                    node_n.g = cost
	        else:
	            continue
	    return node_new
	else:
	    return None

在这里插入图片描述

4 Matlab算法实现

核心代码如下所示

function [new_node, flag] = get_nearest(node_list, node, map, param)
%@breif: Get the node from `node_list` that is nearest to `node`.
    flag = false;
    % find nearest neighbor
    dist_vector = dist(node_list(:, 1:2), node');
    [~, index] = min(dist_vector);
    node_near = node_list(index, :);

    % regular and generate new node
    distance = min(dist(node_near(1:2), node'), param.max_dist);
    theta = angle(node_near, node);
    new_node = [node_near(1) + distance * cos(theta), ...
                           node_near(2) + distance * sin(theta), ...
                           node_near(3) + distance, ...
                           node_near(1:2)];

    % obstacle check
    if is_collision(new_node(1:2), node_near(1:2), map, param)
        return
    end
    
    %  rewire optimization
    [node_num, ~] = size(node_list);
    for i=1:node_num
        node_n = node_list(i, :);
        %  inside the optimization circle
        new_dist = dist(node_n(1:2), new_node(1:2)');
        if new_dist < param.r
            cost = node_n(3) + new_dist;
            %  update new sample node's cost and parent
            if new_node(3) > cost && ~is_collision(new_node(1:2), node_n(1:2), map, param)
                new_node(4:5) = node_n(1:2);
                new_node(3) = cost;
            else
                %  update nodes' cost inside the radius
                cost = new_node(3) + new_dist;
                if node_n(3) > cost && ~is_collision(new_node(1:2), node_n(1:2), map, param)
                    node_list(i, 4:5) = new_node(1:2);
                    node_list(i, 3) = cost;
                end
            end
        else
            continue;
        end
    end
    
    flag = true;
end