👨‍🎓个人主页：研学社的博客 

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🌈3 Matlab代码实现

🎉4 参考文献

---

💥1 概述

本文内容为：悬索桥的车辆振动用于自动识别车辆的质量、速度和到达时间。

以根据悬索桥上收集的振动数据自动识别关键车辆特性。然而，目前的数值实现与 ref [1] 有一些细微的差异。使用连续模型对桥梁进行建模，以降低与车辆识别相关的计算成本[2，3]。车辆被建模为移动质量以降低计算成本。在下文中，仅对主跨度的垂直运动进行建模。该算法适用于交通流量较少的偏远地区的桥梁。

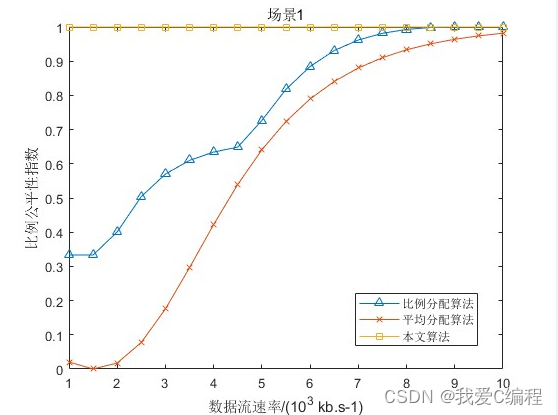
📚2 运行结果

 

 

 

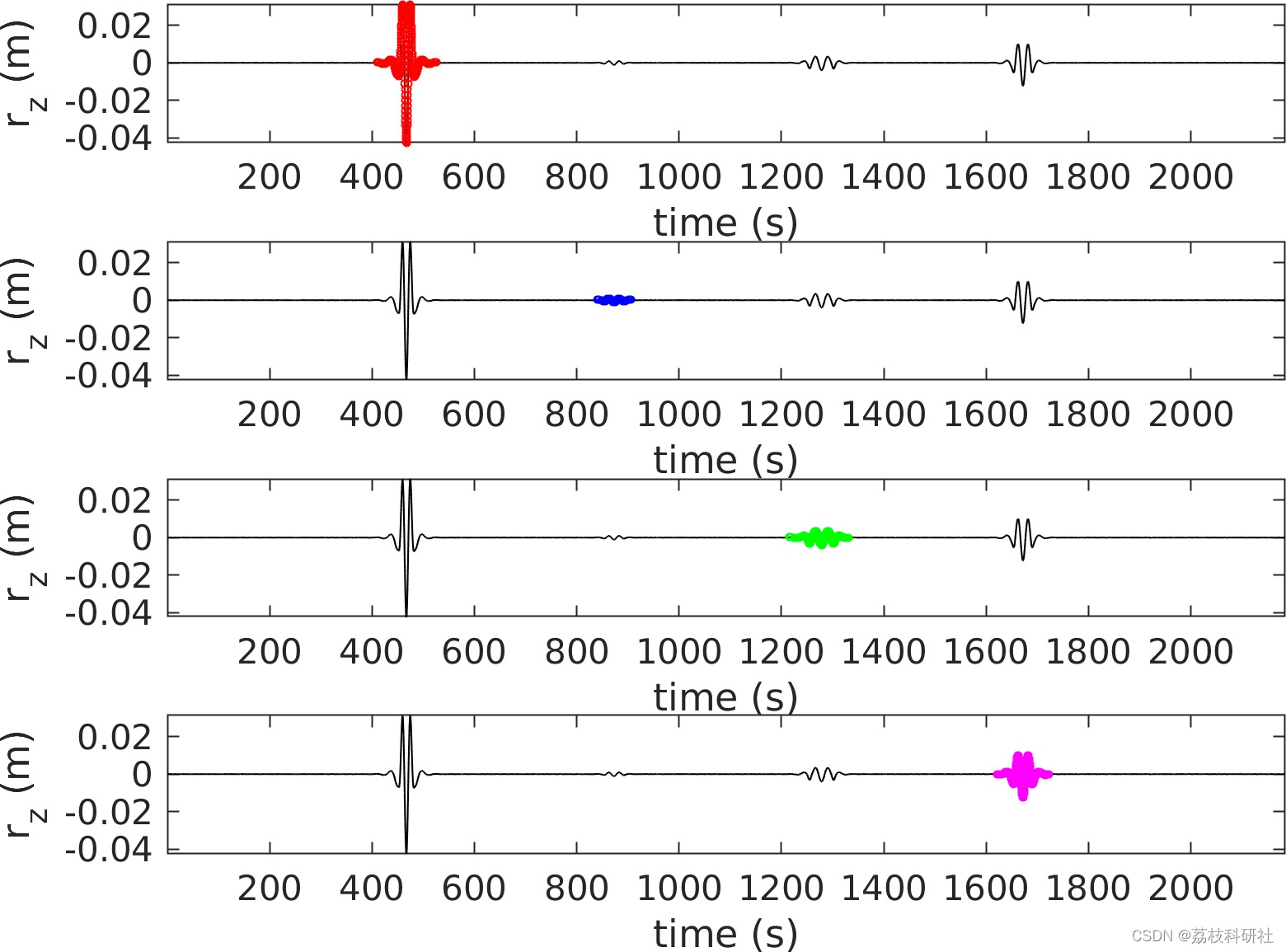
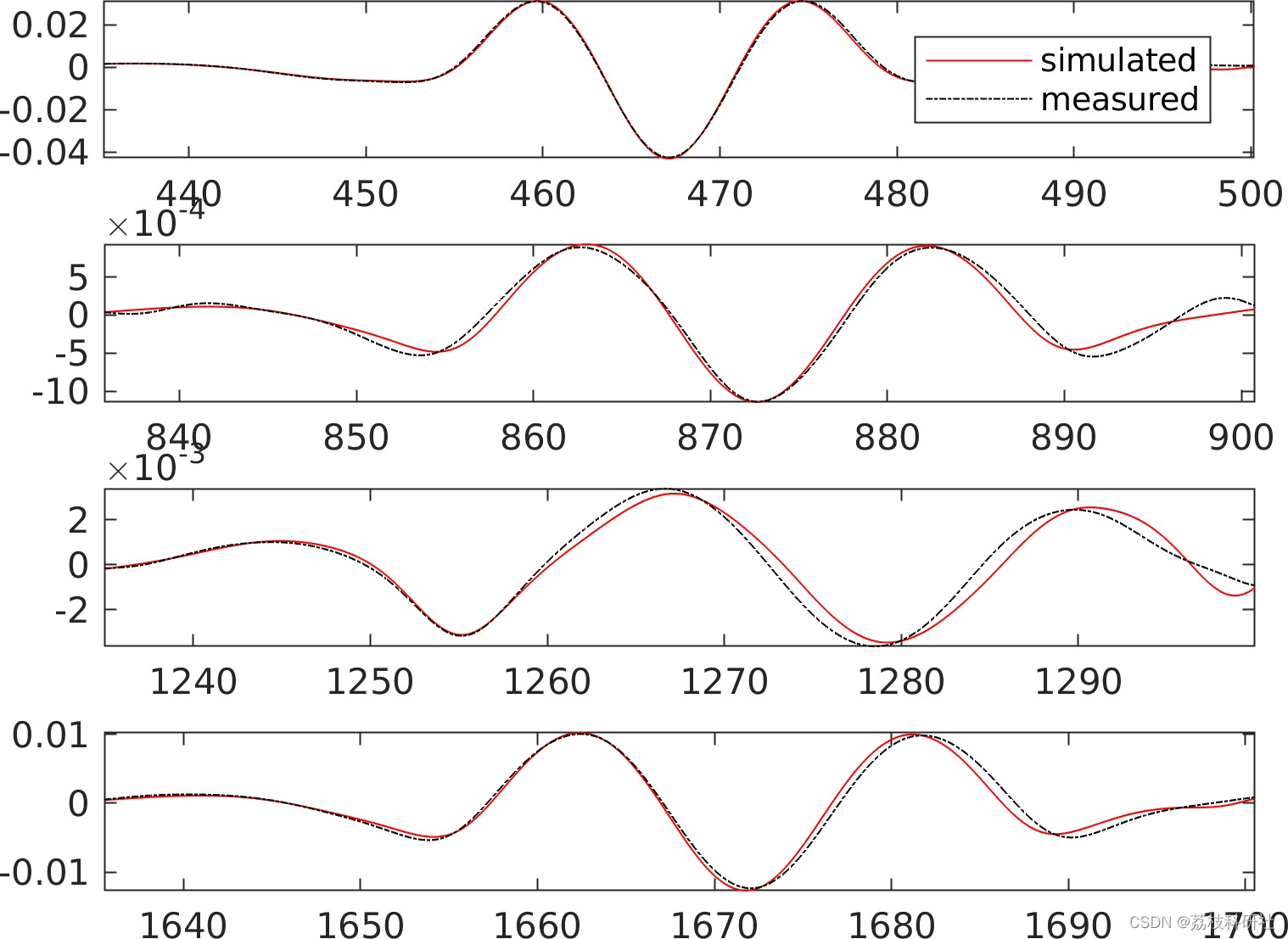
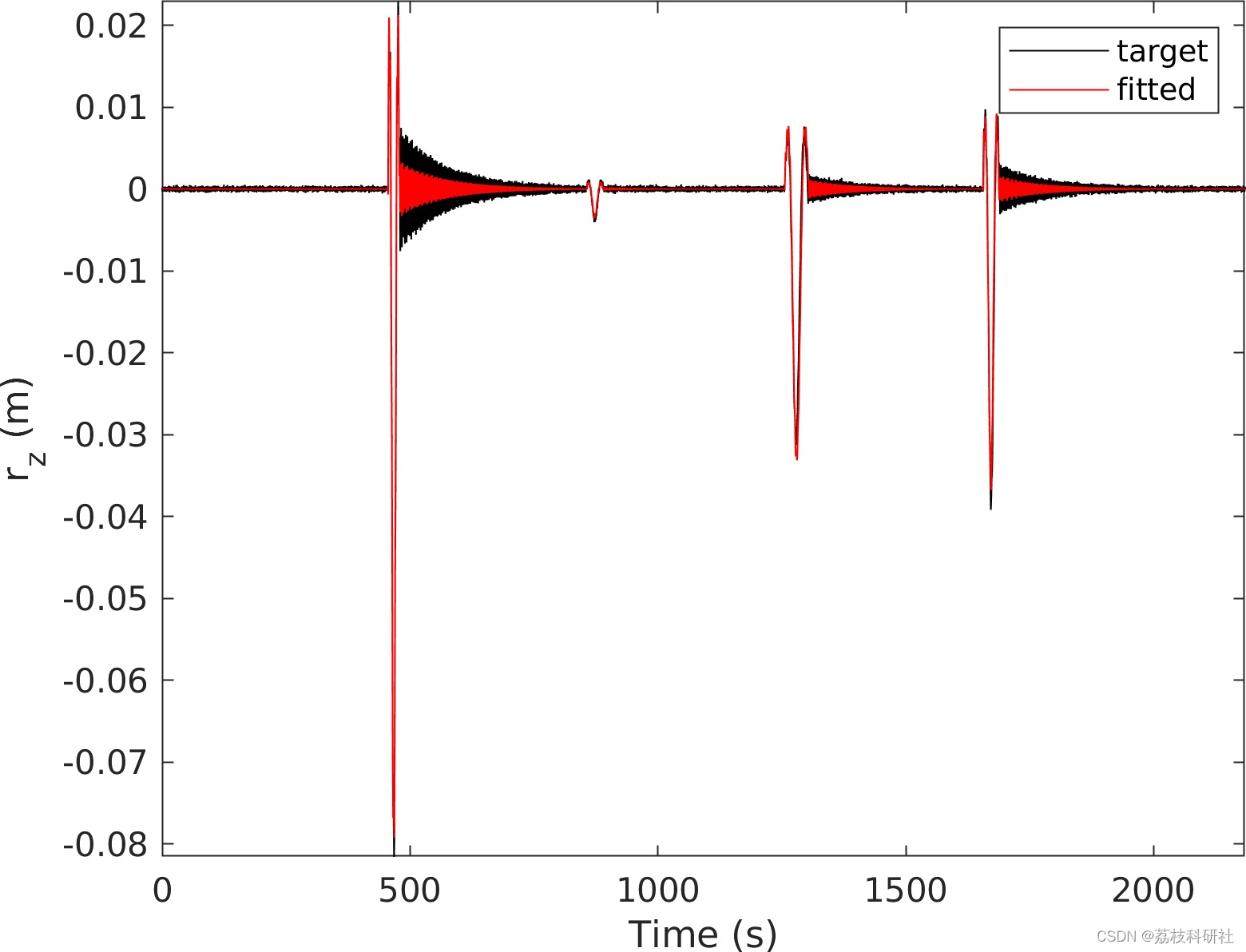
部分代码：

%% Inputparseer
p = inputParser();
p.CaseSensitive = false;
p.addOptional('orderFilt',4);
p.addOptional('fcUp',0.15);
p.addOptional('fcLow',0.04);
p.addOptional('newN',200);
p.addOptional('deltaT',30);
p.addOptional('meanU',0);
p.addOptional('plotData',1);
p.addOptional('RMSE_threshold',0.3);
p.parse(varargin{:});
%%%%%%%%%%%%%%%%%%%%%%%%%%
newN = p.Results.newN ;
orderFilt = p.Results.orderFilt ;
fcUp = p.Results.fcUp;
fcLow = p.Results.fcLow;
deltaT = p.Results.deltaT;
meanU = p.Results.meanU;
plotData = p.Results.plotData;
RMSE_threshold = p.Results.RMSE_threshold;
%% Definition of constants and fundamental parameters
g = 9.81; % accleration of gravity
guess = 3000; % mass speed initial guess

[Nsensors,N]= size(Doz);
if Nsensors>1 && N==1
    Doz = Doz';
    [Nsensors,N]= size(Doz);
else
    error('This version of the code does not include the possibility to include multiple accelerometers');
end

if numel(posAcc) ~=Nsensors, error('numel(posAcc) ~= size(DOz,1)'); end
[~,indY] = min(abs(posAcc-Bridge.x));

%% Fitting algorithm

options=optimset('TolX',1e-6,'TolFun',1e-6,'Display','off'); % increase the fitting precision if Suw = 0
Nvehicle = numel(tImpact);
myMass = zeros(1,Nvehicle);
rmse = zeros(1,Nvehicle);
modelFun = @getVehiclePara;
Direction = nan(1,Nvehicle);

if plotData==1,    figure;end

for ii=1:Nvehicle
    
    [Nsensors,N]= size(Doz);
    t1 = tImpact(ii)-2/3*deltaT; % get lower boundary for simulation start
    t2 = tImpact(ii)+3/2*deltaT; % get upper boundary for simulation stop
    newT = linspace(t1,t2,newN);
    newFs = 1/median(diff(newT));
    rz = interp1(t,Doz,newT);
    rz = filterMyData(rz(:)',newFs,orderFilt,fcUp,fcLow);
    % Check if there exist NaNs
    if any(isnan(rz)), warning('There exist nans values in the rz time series. Consider replacing them by interpolated values'); end
    
    newSpeed = vehicleSpeed(ii);
    % We assume that the turbulent load is negligible for the fitting
    Wind.u = meanU + zeros(Bridge.Nyy,newN); % Include mean wind speed if needed
    Wind.w = zeros(Bridge.Nyy,newN);
    Wind.t = newT;
    speed = newSpeed; % speed of each vehicle
    tStart = tImpact(ii); %
    
    % we initially assume that the vehicle direction is known
    vehicleDirection = 1;
    [myMass(ii)] = lsqcurvefit(@(para,t) modelFun(para,newT(:)),...
        guess,newT(:),rz(:),100,1e5,options);
    
    dummy = modelFun(abs(myMass(ii)),newT);
    myRMSE = RMSE(reshape(rz(:),[],1)./max(abs(rz(:))),dummy(:)./max(abs(dummy)));
    fprintf(['RMSE value is ',num2str(myRMSE,2),'. \n']);
    
    % If the RMSE is larger than the acceptable threshold value, this may be
    % due to the wrong assessement of the vehicle direction
    if myRMSE>RMSE_threshold
        fprintf(['RMSE value is ',num2str(myRMSE,2),'. New attempt is made by changing the vehicle direction \n']);
        vehicleDirection = -1;
        myMass(ii) = nlinfit(newT(:)',rz(:)',modelFun,guess,options);
        dummy = modelFun(abs(myMass(ii)),newT);
        myRMSE = RMSE(rz(:)./max(abs(rz(:))),dummy(:)./max(abs(dummy)));
        fprintf(['new RMSE value is ',num2str(myRMSE,2),'. \n']);
    end
    
    Direction(ii) = vehicleDirection;
    rmse(ii) = RMSE(rz(:),modelFun(myMass(ii),newT));
    
    if plotData==1
        dummy = reshape(modelFun(myMass(ii),newT),[],Nsensors)';
        subplot(Nvehicle,1,ii)
        plot(newT,dummy,'r',newT,rz,'k-.');
        if ii==1
            legend('simulated','measured','location','best');
        end
        set(gcf,'color','w')
        axis tight
    end
end

if nargout==3
    varargout{1} = Direction;
end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

    function [myDo] = getVehiclePara(para,t,varargin)
        p = inputParser();
        p.CaseSensitive = false;
        p.addOptional('rho',1.25);
        p.addOptional('k',1/4);
        p.parse(varargin{:});
        % shorthen the variables name
        rho  = p.Results.rho ;
        k  = p.Results.k ;
        %%
        Ncar = numel(para);
        for pp=1:Ncar
            vehicle(pp).mass = para(pp);
            vehicle(pp).speed = speed(pp,:);
            vehicle(pp).tStart = tStart(pp);
            vehicle(pp).direction = vehicleDirection;
        end
        
        % shortened variable
        D = Bridge.D;
        B = Bridge.B;
        Cd = Bridge.Cd;
        Cl = Bridge.Cl;
        Cm = Bridge.Cm;
        dCd = Bridge.dCd;
        dCl = Bridge.dCl;
        dCm =Bridge.dCm;
        phi = Bridge.phi;
        wn = Bridge.wn;
        zetaStruct = Bridge.zetaStruct;
        u = Wind.u;
        w = Wind.w;
        
        dt = median(diff(t));
        N1 = numel(t);
        
        % Definition of Nyy, and Nmodes:
        [~,Nmodes,Nyy]= size(Bridge.phi);
        
        if max(Bridge.x)== 1
            y = Bridge.x.*Bridge.L;
        else
            warning('Bridge.x is not normalized');
        end
        
        %% MODAL MASS AND STIFNESS CALCULATION
        Mtot = diag([Bridge.m+2*Bridge.mc,Bridge.m+2*Bridge.mc,Bridge.m_theta]);
        phi0 = reshape(phi,[],Nyy);
        phi0_N = bsxfun(@times,phi0,1./max(abs(phi0),[],2));
        Nm = size(phi0,1);
        Mtot = repmat(Mtot,round(Nm/3),round(Nm/3));
        M = zeros(Nm+Ncar);
        K = zeros(Nm+Ncar);
        C = zeros(Nm+Ncar);
        for pp=1:Nm
            for qq=1:Nm/3
                if (pp+3*qq)<=Nm
                    Mtot(pp,pp+3*qq) = 0;
                    Mtot(pp+3*qq,pp) = 0;
                end
            end
            for qq=1:Nm
                M(pp,qq)  = trapz(y,phi0_N(pp,:).*phi0_N(qq,:).*Mtot(pp,qq));
            end
        end
        K(1:Nm,1:Nm) = diag(wn(:)).^2*M(1:Nm,1:Nm);
        C(1:Nm,1:Nm) = 2.*diag(wn(:))*M(1:Nm,1:Nm)*diag(zetaStruct(:));
        
        %% PREALLOCATION
        CoeffAero = @(C,alpha) C(1)+alpha.*C(2); % linear
        C1=[Cd,dCd];
        C2=[Cl,dCl];
        C3=[Cm,dCm];
        %% INITIALISATION
        Do = zeros(3,Nyy,N1);
        Ao = zeros(3,Nyy,N1);
        Aoz_car = zeros(Ncar,N1);
        rt=zeros(Nyy,1);
        dry=zeros(Nyy,1);
        drz=zeros(Nyy,1);
        drt=zeros(Nyy,1);
        
        % Case of no wind
        if mean(nanstd(u,0,2))<0.01 && mean(nanstd(w,0,2))<0.01 && nanmean(nanmean(u,2))<0.1
            noWind=1;
        else
            noWind=0;
        end
        
        for idt=1:N1
            Fmodal_wind = zeros(Nm);
            % get  modal forces
            if noWind==0 % if wind turbulence is acounted for
                [Fmodal_wind(1:Nm,1:Nm)]= getFmodal(CoeffAero,C1,C2,C3,y,...
                    u(:,idt),w(:,idt),dry,drz,drt,D,B,rt,k,rho,Nmodes,phi0_N);
                if Ncar>0
                    Fmodal_wind(Nm+1:end,Nm+1:end)=0; % ensure that there is no wind load on the car
                end
            else
                Fmodal_wind = zeros(Nm+Ncar);
            end
            
            if Ncar>0
                [Fmodal_car] = getVehicleLoad(t,vehicle,Bridge,Nm,y,phi0_N,idt);
                Fmodal = Fmodal_wind+ Fmodal_car; % load on the bridge
            else
                Fmodal = Fmodal_wind;
            end
            
            if idt ==1 % initial acceleration
                DoM = zeros(Nm);
                VoM = zeros(Nm);
                AoM = M(1:Nm,1:Nm)\(Fmodal(1:Nm,1:Nm)-C(1:Nm,1:Nm).*VoM-K(1:Nm,1:Nm).*DoM);
                [DoM,VoM,AoM,Do(:,:,idt),Vo,Ao(:,:,idt),Aoz_car(:,idt),~] =...
                    Newmark(dt,DoM,VoM,AoM,Fmodal(1:Nm,1:Nm),M(1:Nm,1:Nm),K(1:Nm,1:Nm),C(1:Nm,1:Nm),phi0,Ncar,Nyy,Nm);
            else
                [DoM,VoM,AoM,Do(:,:,idt),Vo,Ao(:,:,idt),Aoz_car(:,idt),~] =...
                    Newmark(dt,DoM,VoM,AoM,Fmodal(1:Nm,1:Nm),M(1:Nm,1:Nm),K(1:Nm,1:Nm),C(1:Nm,1:Nm),phi0,Ncar,Nyy,Nm);
            end
            
            rt = Do(3,:,idt)';
            dry = Vo(1,:)';
            drz = Vo(2,:)';
            drt = Vo(3,:)';
        end
        
        dummy0 = detrend(squeeze(Do(2,indY,:)))';
        [myDo] = filterMyData(dummy0(:)',newFs,orderFilt,fcUp,fcLow);
        myDo = myDo(:);
    end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    function [Fmodal]= getFmodal(CoeffAero,C1,C2,C3,y,u,w,dry,drz,drt,...
            D,B,rt,k,rho,Nmodes,phi0_N)
        % [Fmodal]= getFmodal(y,u,w,dry,drz,drt,D,B,rt) computes the modal
        %  forces acting on the main-span of a suspension bridge bridge deck
        %%
        Vrel = (u-dry);
        W = (w-drz-k*B.*drt);
        Vrel = sqrt(Vrel.^2+W.^2); % is [Nyy x 1]
        beta = atan(W./Vrel); % is [Nyy x 1]
        alpha = rt+beta; % is [Nyy x N]
        COEFF = 1/2*rho*B.*Vrel.^2;
        Ftot(:,1)=COEFF.*(D/B.*CoeffAero(C1,alpha).*cos(beta) - CoeffAero(C2,alpha).*sin(beta));
        Ftot(:,2)=COEFF.*(D/B.*CoeffAero(C1,alpha).*sin(beta) +  CoeffAero(C2,alpha).*cos(beta));
        Ftot(:,3)=COEFF.*(B.*CoeffAero(C3,alpha));
        F = repmat(Ftot,1,Nmodes)';
        Fmodal = trapz(y,F.*phi0_N,2);
        Fmodal = diag(Fmodal(:));
    end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    function [x1,dx1,ddx1,Do,Vo,Ao,Aoz_car,Doz_car] =...
            Newmark(dt,x0,dx0,ddx0,F,M,K,C,phi0,Ncar,Nyy,Nm,varargin)
        %% options: default values
        inp = inputParser();
        inp.CaseSensitive = false;
        inp.addOptional('alpha',1/4);
        inp.addOptional('beta',1/2);
        inp.parse(varargin{:});
        % shorthen the variables name
        alphaCoeff = inp.Results.alpha ;
        beta = inp.Results.beta;

🌈3 Matlab代码实现

🎉4 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1] Cheynet, E., Daniotti, N., Jakobsen, J. B., & Snæbjörnsson, J. (2020). Improved long‐span bridge modeling using data‐driven identification of vehicle‐induced vibrations. Structural Control and Health Monitoring, volume 27, issue 9. https://doi.org/10.1002/stc.2574

[2] E. Cheynet. ECheynet/EigenBridge v3.3. Zenodo, 2020, .