1.算法描述

无线接入技术发展迅速，异构网络并存的现象普遍存在；同时，随着终端用户数量的剧增、业务类型的多样化和高服务质量多媒体数据业务需求的增加，通过异构网络进行高速和高效地协作传输成为无线通信领域非常重要的课题之一。

针对异构网络的协作传输和协作速率分配的研究在近几年得到了广泛关注，但异构无线接入网络在传输能力、网络状态和资源利用率等方面的差异性没有充分考虑，仍有很多问题需要进一步探讨研究，也为广大研究者提出了挑战。

异构无线网络环境中的协作接入和协作速率分配的研究在不断深入，从研究方法上可分为以下三种：

1）总体效用最优方案

该方案中只有一个决策者，它根据多业务流传输时用户感知的总服务质量或者总的网络收益确定速率分配方案，也称为全体最优（Social Optimum）。目前的研究成果主要有：针对多媒体通信，用估算的可用带宽和延时计算视频流的扭曲度，以异构网络中视频流的总扭曲度最小为优化目标，设计了一种分布式速率分配算法。引入支持相量机（SVM）预测丢包率和多跳网络中端到端视频流传输的扭曲度，据此用一个非凸优化问题对资源分配进行数学建模，并采用拉格朗日型对偶定理对全局优化问题进行了求解。还有以引入了接入无线信道时单位流量的价格，并提出了一种基于代价的网络总收益最优的多跳网络资源分配方案，从而获得最优的资源利用，并实现了接入业务流的公平竞争。

2）非合作传输方案

作为协作传输的理性参与者，在资源分配的过程中各网络会力图最大化自身的收益或减小代价，这体现了参与者之间的竞争性和利己性。近几十年发展起来的非合作博弈理论为这种竞争场景中的资源分配提供了多种数学模型，在通信领域得到了广泛应用，如竞争用户的功率分配、扩频码分配和软件无线电中的频谱分配等资源管理。

针对未授权频段无线接入网络的多样性和共存性，无线网络作为参与者不断交互并试图最大化自身效益，采用基于网络状态的博弈论模型（Stage-basedgame）对各网络的竞争和资源分配建模，并采用福利社会中微观经济理论对该模型进行分析和求解。

3）合作传输方案

通过异构网络协作传输，目的是为了充分利用多网络资源实现合作传输，满足人们对高速多媒体业务的需求。因此，以网络作为理性参与者，它们之间除了竞争的关系，还存在合作关系，近年来发展起来的合作博弈论描述了参与者之间的合作形成机制，逐渐被用于对协作接入的速率分配进行建模。协作接入的目的是把高速业务流分发到异构网络进行并发合作传输，提高服务质量，这类似于经济学中破产后的公司资产分配问题，网络之间形成联盟确保传输需求得到满足。

近年来，国内外学者在异构网络技术无缝连接与协同工作等方面不断开展研究，研究重点逐渐从网络选择，垂直切换，流量均衡，发展到异构网络的协作传输。事实上，不少异构网络可共存，它们在使用频段上相互错开，或者通过跳频技术进行避让。如果能根据业务需求和网络状态来控制用户的多业务在多网络的接入与资源调度，就可以通过网络协作提高传输能力。

其中，速率分配就是把数据流拆分到多个网络进行协作传输，相关研究已引起不少学者的关注。文献中采用博弈论的方法并结合网络传输能力和公平性原则进行资源分配。上述研究以网络吞吐量最大为优化目标，没有考虑网络的接入时间代价(接入机制决定) 和不同网络资源利用效率的差异。此外，当请求传输的业务流速率较小时，要求所有网络参与协作传输是低效的，此时数据包分拆和重组的代价不能忽略。使用基于供需关系的代价函数来实现多视频，流的速率分配L 网络资源的供求关系决定了它们在接入难度资源利用效率等方面也不尽相同。

2.仿真效果预览

matlab2022a仿真如下：

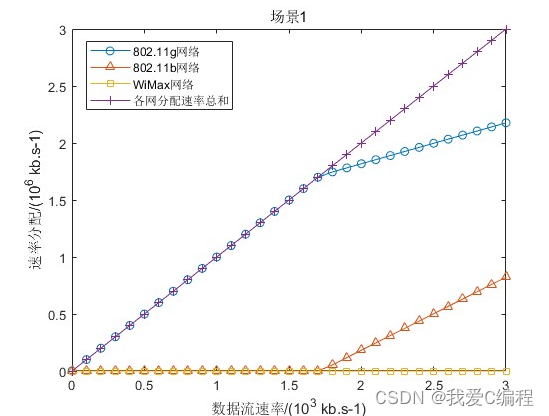
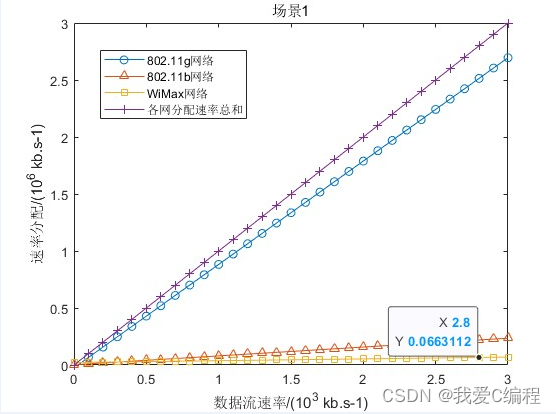
从仿真图中可见，3个接入网的资源占用情况不同，802.11g的信道利用率最低，网络负载最轻，业务流倾向于选择信道利用率低的网络进行接入：当业务流速率低于1.1Mb/s时，仅IEEE802.11g网络被选用并进行传输，相对重载的IEEE802.11b没有数据传输，避免了接入用户数增多而导致的碰撞率增大，因为可用带宽低，WIMAX直到业务流速率需求超过2.1Mb/s时才参与合作传输。

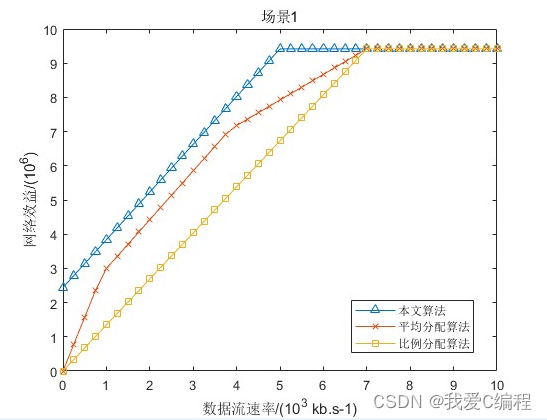
从图2可知，当时，不同算法的吞吐量收益相同，文中算法获得的网络总效益最大，即接入代价最小；当网络的信道利用率相同时，文中算法和根据频谱效率按比例分配的算法等同，MT 获得的网络总效益相同；随着网络信道利用率的差值的增大，采用文中算法的MT获得的网络总效益的优势明显增大。

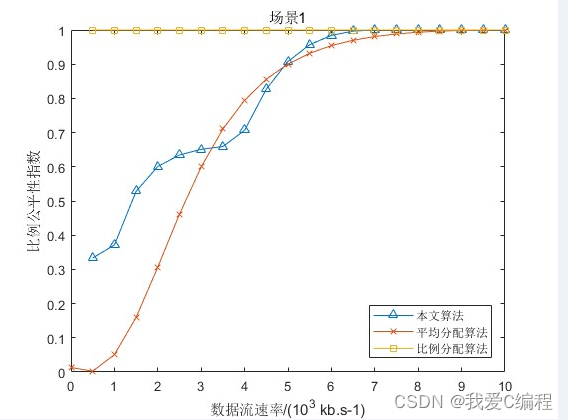
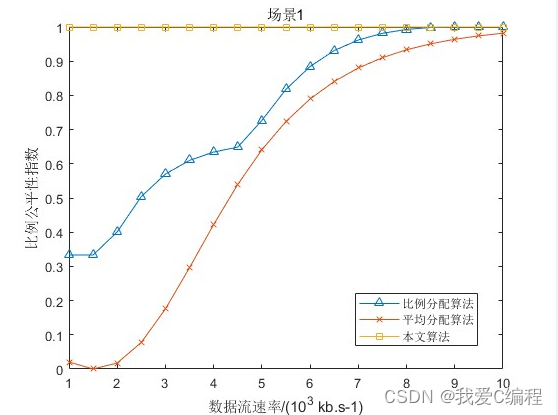
从图 3可知：场景:1中比例分配法的比例公平性指数最优，文中算法的比例公平性指数仅在大部分情况下优于平均分配法; 场景 2 中文中算法的比例公平性指数与比例分配法相同，传输速率按比例均衡分配。

3.MATLAB核心程序

miu1  = 2.5;
miu2  = 1.4;
miu3  = 0.8;
 
%初始化网络权值
Fz(1) = 1/miu1;
Fz(2) = 1/miu2;
Fz(3) = 1/miu3;
w     = Fz/sum(Fz);
miu   = [miu1,miu2,miu3];
%仿真尺度
Stime = [0:0.1:3];
 
%开始循环
Ind = 0;
for i = Stime
    Ind     = Ind + 1;
    %计算剩余贷款
    LBS1(Ind) = w(1)*(sum(miu)-i);
    LBS2(Ind) = w(2)*(sum(miu)-i);
    LBS3(Ind) = w(3)*(sum(miu)-i);
    %进行速率的分配
    x1(Ind)   = miu1 - LBS1(Ind);
    x2(Ind)   = miu2 - LBS2(Ind);
    x3(Ind)   = miu3 - LBS3(Ind);
 
    %N=3;
    if LBS3(Ind) > miu3 
       x3(Ind)   = 0;
       w1        = Fz/sum(Fz(1:2));
       LBS1(Ind) = w1(1)*(LBS1(Ind)/w(1) - miu3);
       LBS2(Ind) = w1(2)*(LBS2(Ind)/w(2) - miu3);
       %进行速率的分配
       x1(Ind)   = miu1 - LBS1(Ind);
       x2(Ind)   = miu2 - LBS2(Ind);
    end
    if LBS2(Ind) > miu2 
       x2(Ind)   = 0;
       w11       = Fz/sum(Fz(1));
       LBS1(Ind) = w11(1)*(LBS1(Ind)/w1(1)-miu2);
       %进行速率的分配
       x1(Ind)   = miu1 - LBS1(Ind);
    end
end
01_101m