文章目录
- 1. 二叉树的最大深度【简单】
- 1.1 题目描述
- 1.2 解题思路
- 1.3 代码实现
- 2. 对称二叉树【简单】
- 2.1 题目描述
- 2.2 解题思路
- 2.3 代码实现
- 3. 二叉树的直径【简单】
- 3.1 题目描述
- 3.2 解题思路
- 3.3 代码实现
- 4. 验证二叉搜索树【中等】
- 4.1 题目描述
- 4.2 解题思路
- 4.3 代码实现
- 5. 最小路径和【中等】
- 5.1 题目描述
- 5.2 解题思路
- 5.3 代码实现
1. 二叉树的最大深度【简单】
题目链接:https://leetcode.cn/problems/maximum-depth-of-binary-tree/
参考题解:https://leetcode.cn/problems/maximum-depth-of-binary-tree/solution/er-cha-shu-de-zui-da-shen-du-by-leetcode-solution/
1.1 题目描述
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],

返回它的最大深度 3 。
1.2 解题思路
1.3 代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode* root) {
if(!root)
return 0;
return max(maxDepth(root->left), maxDepth(root->right)) + 1;
}
};
2. 对称二叉树【简单】
题目链接:https://leetcode.cn/problems/symmetric-tree/
参考题解:https://leetcode.cn/problems/symmetric-tree/solution/dui-cheng-er-cha-shu-by-leetcode-solution/
2.1 题目描述
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
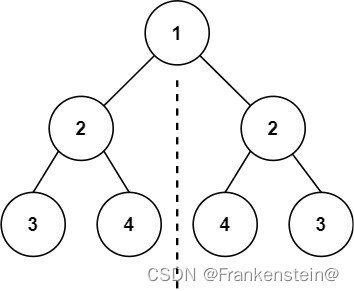
输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:
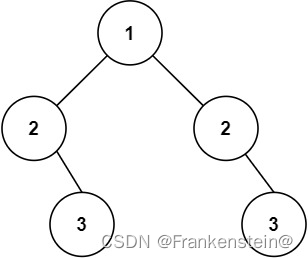
输入:root = [1,2,2,null,3,null,3]
输出:false
提示:
- 树中节点数目在范围 [1, 1000] 内
- -100 <= Node.val <= 100
进阶: 你可以运用递归和迭代两种方法解决这个问题吗?
2.2 解题思路
2.3 代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool checkSymmetric(TreeNode* left, TreeNode* right) {
if(!left && !right)
return true;
if(!left || !right)
return false;
if(left->val == right->val)
return checkSymmetric(left->left, right->right) && checkSymmetric(left->right, right->left);
else
return false;
}
bool isSymmetric(TreeNode* root) {
return checkSymmetric(root, root);
}
};
3. 二叉树的直径【简单】
题目链接:https://leetcode.cn/problems/diameter-of-binary-tree/
参考题解:https://leetcode.cn/problems/diameter-of-binary-tree/solution/er-cha-shu-de-zhi-jing-by-leetcode-solution/
3.1 题目描述
给你一棵二叉树的根节点,返回该树的 直径 。
二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。
两节点之间路径的 长度 由它们之间边数表示。
示例 1:
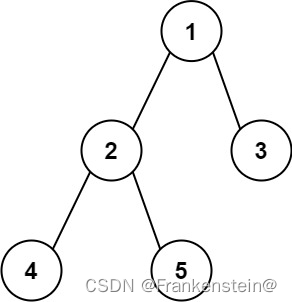
输入:root = [1,2,3,4,5]
输出:3
解释:3 ,取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。
示例 2:
输入:root = [1,2]
输出:1
提示:
- 树中节点数目在范围 [1, 10^4] 内
- -100 <= Node.val <= 100
3.2 解题思路
3.3 代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int findSubMaxLen(TreeNode* root, int& ans) {
if(!root)
return 0;
int leftMax = findSubMaxLen(root->left, ans);
int rightMax = findSubMaxLen(root->right, ans);
ans = max(ans, leftMax + rightMax + 1);
return max(leftMax, rightMax) + 1;
}
int diameterOfBinaryTree(TreeNode* root) {
int ans = 1;
findSubMaxLen(root, ans);
return ans - 1;
}
};
4. 验证二叉搜索树【中等】
题目链接:https://leetcode.cn/problems/validate-binary-search-tree/
参考题解:https://leetcode.cn/problems/validate-binary-search-tree/solution/yan-zheng-er-cha-sou-suo-shu-by-leetcode-solution/
4.1 题目描述
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
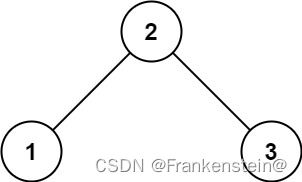
输入:root = [2,1,3]
输出:true
示例 2:
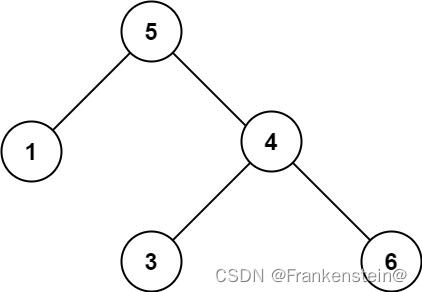
输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
提示:
- 树中节点数目范围在[1, 10^4] 内
- -2^31 <= Node.val <= 2^31 - 1
4.2 解题思路
4.3 代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool checkBST(TreeNode* root, long long lower, long long upper) {
if(!root)
return true;
if(root->val <= lower || root->val >= upper)
return false;
return checkBST(root->left, lower, root->val) && checkBST(root->right, root->val, upper);
}
bool isValidBST(TreeNode* root) {
return checkBST(root, LONG_MIN, LONG_MAX);
}
};
5. 最小路径和【中等】
题目链接:https://leetcode.cn/problems/minimum-path-sum/
参考题解:https://leetcode.cn/problems/minimum-path-sum/solution/zui-xiao-lu-jing-he-by-leetcode-solution/
5.1 题目描述
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明: 每次只能向下或者向右移动一步。
示例 1:
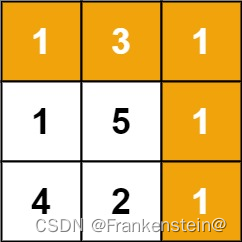
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:grid = [[1,2,3],[4,5,6]]
输出:12
提示:
- m == grid.length
- n == grid[i].length
- 1 <= m, n <= 200
- 0 <= grid[i][j] <= 200
5.2 解题思路
5.3 代码实现
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int rows = grid.size();
int cols = grid[0].size();
vector<vector<int>> ans(rows, vector<int>(cols));
for(int row = 0; row < rows; row++) {
for(int col = 0; col < cols; col++) {
if(!row && !col)
ans[row][col] = grid[row][col];
else if(!row)
ans[row][col] = ans[row][col - 1] + grid[row][col];
else if(!col)
ans[row][col] = ans[row - 1][col] + grid[row][col];
else {
ans[row][col] = min(ans[row - 1][col], ans[row][col - 1]) + grid[row][col];
}
}
}
return ans[rows - 1][cols - 1];
}
};