1.对应letecode链接
高楼扔鸡蛋问题

2.题目描述

解题思路

题目是这样：你面前有一栋从 1 到 N 共 N 层的楼，然后给你 K 个鸡蛋（K 至少为 1）。现在确定这栋楼存在楼层 0 <= F <= N，在这层楼将鸡蛋扔下去，鸡蛋恰好没摔碎（高于 F 的楼层都会碎，低于 F 的楼层都不会碎）。现在问你，最坏情况下，你至少要扔几次鸡蛋，才能确定这个楼层 F 呢？
也就是让你找摔不碎鸡蛋的最高楼层 F，但什么叫最坏情况下至少要扔几次呢？我们分别举个例子就明白了。我们首先不用理这个鸡蛋的个数，现在假设有8层楼。我们在第一层楼开始扔这个鸡蛋。如果没碎那么我们就可以接着第二层扔这个鸡蛋，如果还没碎我们可以接着第三层开始扔。如果一直没碎的话我们最坏的情况下是不是需要尝试这个8次。而至少需要扔几次这又是什么意思？因为我们可以选择在第几号楼开始扔这个鸡蛋。假设我们现在在s层楼开始扔鸡蛋无非就只有两种情况一种是这个碎了，另外一种就是没碎。如果碎了的话那么答案只有可能在s-1层中，如果没碎那么答案在这个n-s层之中.在这一层开始扔的答案就是这个这两种情况下最坏的那种。随着我们开始扔鸡蛋层数的不同那么这个最话的这个结果也肯定不同。那么只需要在这么多结果当中选择代价最少的那种就可以了。

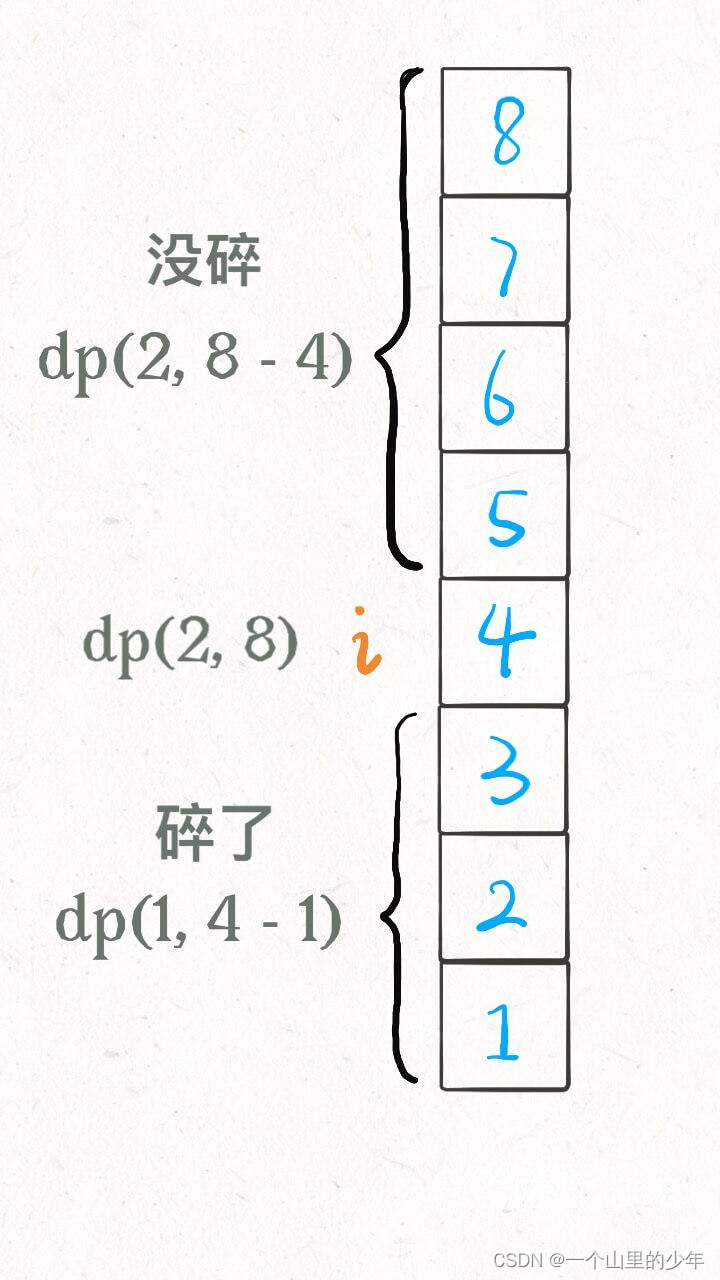
在这里需要注意的是如果鸡蛋没碎那么这个第i层我们可以将其当中这个第0层。下面我们来看看这个代码如何来书写。

class Solution {
  public:
    int superEggDrop(int k, int n) {
        return process(k, n);
    }
    //一共有n层楼k个鸡蛋返回最小扔鸡蛋的次数
    int process(int k, int n) {
        //如果只有一个鸡蛋那么最坏的情况下肯定是需要扔k层的
        if (k == 1) {
            return n;
        }
        //0层楼不用试肯定是0次
        if (n == 0) {
            return 0;
        }
        int ans = INT_MAX;
        for (int i = 1; i <= n; i++) {
            //枚举所有开始扔鸡蛋的层数在所有结果当中选择代价最小的一个
            ans = min(ans, max(process(k - 1, i - 1), process(k, n - i)) + 1);
        }
        return ans;
    }
};

但是这样很暴力即使我们加了这个记忆化搜索我们也过不了。下面我们看看这个记忆化搜索的代码如何实现。

class Solution {
  public:
     vector<vector<int>>dp;
    int superEggDrop(int k, int n) {
        dp.resize(k+1,vector<int>(n+1,-1));
        return process(k, n);
    }
    //一共有n层楼k个鸡蛋返回最小扔鸡蛋的次数
    int process(int k, int n) {
        //如果只有一个鸡蛋那么最坏的情况下肯定是需要扔k层的
        if (k == 1) {
            return n;
        }
        //0层楼不用试肯定是0次
        if (n == 0) {
            return 0;
        }
        if(dp[k][n]!=-1)
        {
            return dp[k][n];
        }
        int ans = INT_MAX;
        for (int i = 1; i <= n; i++) {
            //枚举所有开始扔鸡蛋的层数在所有结果当中选择代价最小的一个
            ans = min(ans, max(process(k - 1, i - 1), process(k, n - i)) + 1);
        }
        dp[k][n]=ans;
        return ans;
    }
};

下面我们来看看这个方法二：
方法二有点偏数学方法，非常的难想到利用函数单调性进行二分。并不是像刚才那样一层楼一层楼的进行枚举，把枚举的过程做了一点优化。

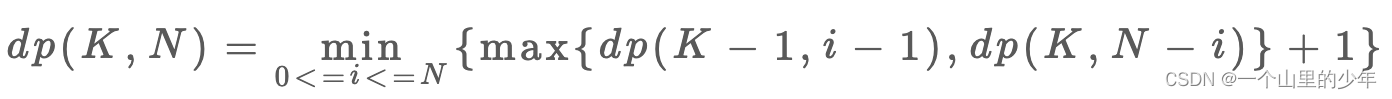
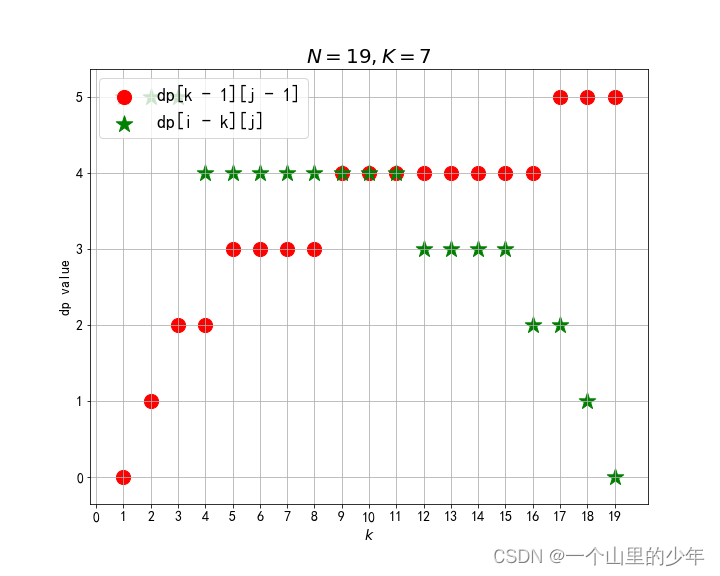
我们可以看到dp(K,N)他只依赖这个。dp（K-1，i-1)和这个dp(K,N-i)如果我们把考虑鸡蛋的个数，而且那么dp(K-1,i-1)是单调递增的函数而这个dp(K,N-i)是这个单调递减的函数。我们要求他们两个的最大值最小的那个。当这两个函数相等的时候这个时候是最优解。下面我们看看这几种情况。

情况 1：最低点只有 1 个点

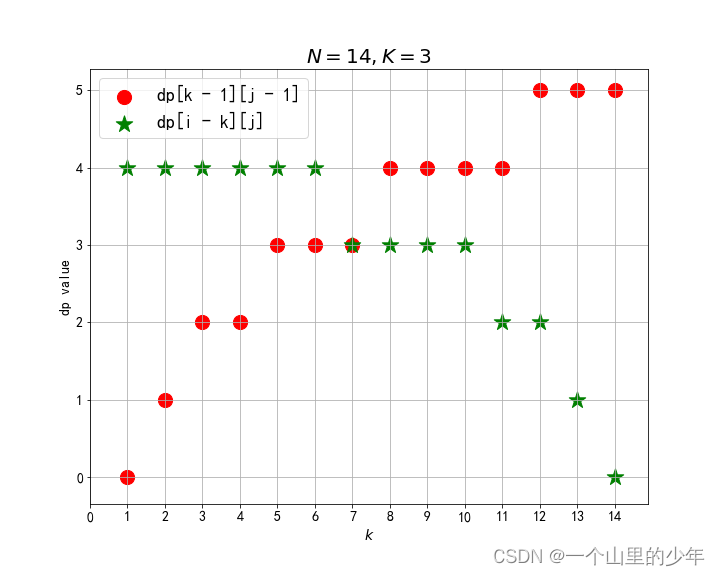
情况 2：最低点是若干个重合的点

情况 3：最低点不重合，但是两边的值一样

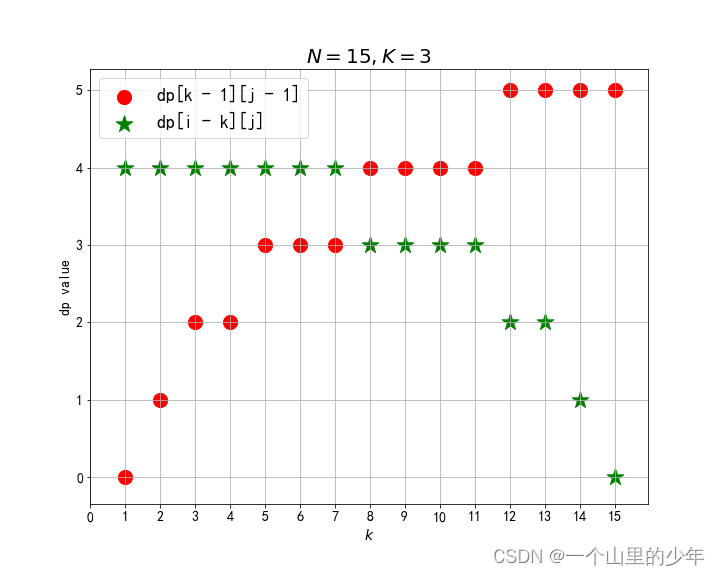
从图上可以看出：二者的较大值的最小点在它们交汇的地方。那么有没有可能不交汇，当然有可能（上面第 3 张图），二者较大值的最小者一定出现在画成曲线段交点的两侧，并且二者的差值不会超过 1，也就是如果没有重合的点，两边的最大值是一样的（从图上看出来的，没有严格证明），因此取左侧和右侧两点中的一点都可以，不失一般性，可以取左边的那个点的 k。也就是找到使得 dp[i - k][j] <= dp[k - i][j - 1] 最大的那个 k 值即可。

下面我们来看看代码如何来书写

class Solution {
public:
    vector<vector<int>>dp;
    int superEggDrop(int k, int n) {
        dp.resize(k+1,vector<int>(n+1,-1));
          return process(k,n);
    }

    int process(int k,int n)
    {
        if(k==1){
            return n;
        }
        if(n==0){
            return 0;
        }
        if(dp[k][n]!=-1)
        {
            return dp[k][n];
        }
        int ans=-1;
        int L=1;
        int R=n;
        //找到这个大于等于这个最大的数字
        while(L<=R)
        {
            int mid=(L+R)/2;
            int l=process(k-1,mid-1);
            int r=process(k,n-mid);
            if(l<=r){
                ans=mid;
                L=mid+1;
            }else{
                R=mid-1;
            }
        }
          //在这一层肯定是这个最优的
        dp[k][n]=max(process(k-1,ans-1),process(k,n-ans))+1;
        return dp[k][n];
    }
};