【POJ No. 1019】数字序列 Number Sequence

北大OJ 题目地址

【题意】

给出单个正整数i ，编写程序以找到位于数字组S 1 , S 2 , …, Sk 序列中第i 位上的数字。每个组Sk 都由一系列正整数组成，范围为1～k ，一个接一个地写入。

序列的前80位数字如下：

11212312341234512345612345671234567812345678912345678910123456789101112345678910

【输入输出】

输入：

第1行包含一个整数t （1≤t ≤10），表示测试用例的数量。每个测试用例后都跟一行，包含单个整数i （1≤i ≤2, 147,483, 647）。

输出：

对每个测试用例，都单行输出第i 位上的数字。

【样例】

【思路分析】

在测试用例中，序列的第8位和第3位都是2：

将每个组都看作一个分块，每个组（分块）的长度都为a [i ]：当组内的每个数都由一位数字组成时，当前组的长度等于前一组的长度+1；当组内出现两位数10～99时，当前组的长度等于前一组的长度+2，以此类推。

• 1 12 123 1234 12345 123456 1234567 12345678 123456789前一组的长度+1
• 12345678910 1234567891011 123456789101112 …… 前一组的长度+2

a [i ]为第i 块的长度，sum[i ]为前i （包括i ）块的总长度。

例如，查询第n 位上的数字，首先定位到第i 块，然后在当前块内查找具体的数k 。

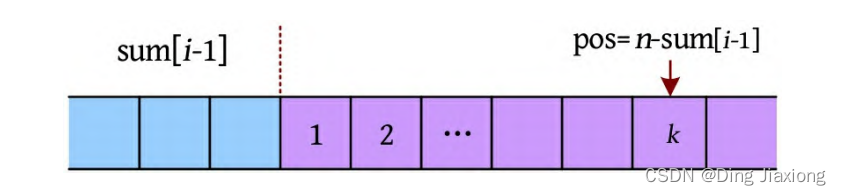
k 可能是多位数，例如k =12406，如下图所示。

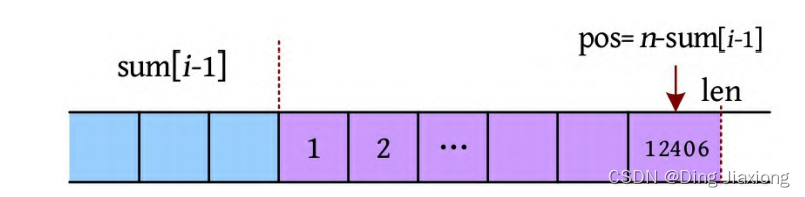
第pos位的数字应为k /10^(len-pos) =124，124%10=4。

【算法设计】

① 计算每一块的长度a [i ]及前i 块的总长度sum[i ]。

② 定位到第i 块，在块内查找第pos位所在的数k。

③ 数k 有可能是多位数，第pos位为k /(int)pow(10.0, len - pos)%10。

【算法实现】

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>

typedef long long LL;

const int maxn=40000;
LL a[maxn],sum[maxn];//a[i]为第i组的长度，sum[i]为前i(包括i)组的总长度

int main(){
    int i,j;
    sum[0]=a[0]=0;
    for(i=1;i<maxn;i++){
        a[i]=a[i-1]+(int)log10((double)i)+1;
        sum[i]=sum[i-1]+a[i];
    }
    int t,n;
    scanf("%d",&t);
    while(t--){
        scanf("%d",&n);
        i=0;
        while(sum[i]<n) i++;  //确定n在第i组
        int pos=n-sum[i-1];  //确定n在第i组的第pos个位置
        int len=0,k=0;
        while(len<pos){
            k++;
            len+=(int)log10((double)k)+1;
        }
        printf("%d\n", k/(int)pow(10.0,len-pos)%10);
    }
    return 0 ;
}