嵌入(Embedding)在机器学习和自然语言处理中是一种表示离散变量(如单词、句子或整个文档)的方式,通常是作为高维向量或者矩阵。嵌入的目标是捕捉到输入数据中的语义信息,使得语义相近的元素在嵌入空间中的距离也比较近。
例如,在自然语言处理中,词嵌入是一种将单词或短语从词汇表映射到向量的技术。这些嵌入向量捕捉了词汇之间的语义和语法关系。例如,词嵌入可以捕捉到"king"和"queen","man"和"woman"之间的相似性,并且可以通过向量运算来表示语言的一些特性,如"king" - "man" + "woman" ≈ "queen"。
嵌入的维度是一个重要的参数,它决定了嵌入向量的大小。较小的维度可能无法捕捉到足够的语义信息,而较大的维度可能导致计算复杂性增加和过拟合的风险。嵌入的维度通常是一个需要调整的超参数,它的选择取决于多种因素,包括数据的复杂性(例如,词汇的大小和语言的复杂性)、模型的复杂性、计算资源的可用性,以及特定任务的需求。
在实际应用中,词嵌入的维度通常选取在几十到几百之间,例如,Word2Vec和GloVe等常用的词嵌入方法通常使用50, 100, 200或300维的嵌入。而在一些更复杂的模型(如BERT或GPT)中,嵌入的维度可能会达到几千。
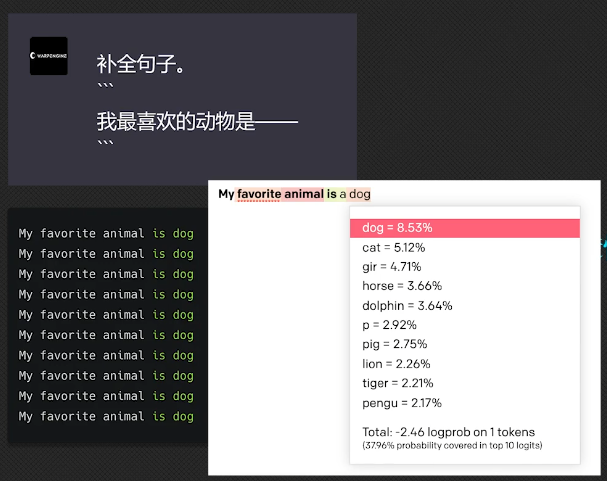
在cookbook里面fine_food_reviews_with_embeddings_1k.csv这个数据集里面我们可以看到embedding如图所示
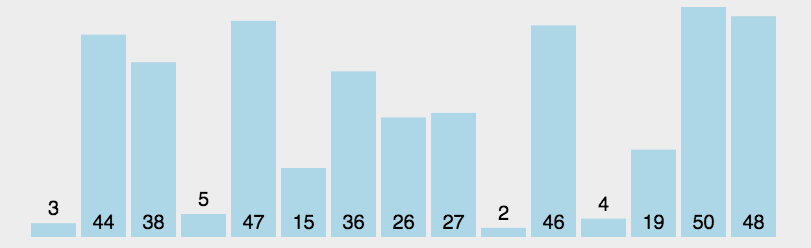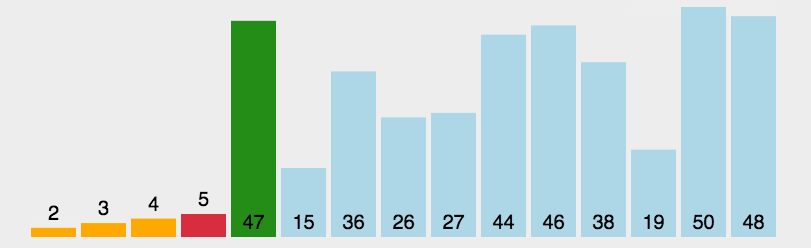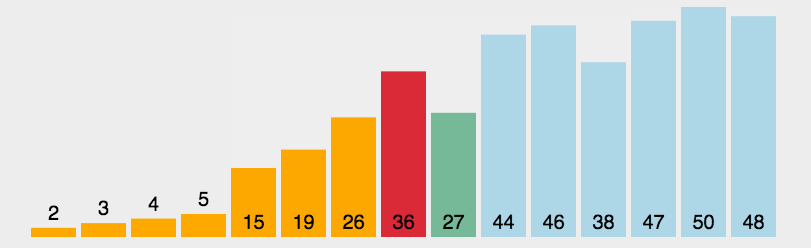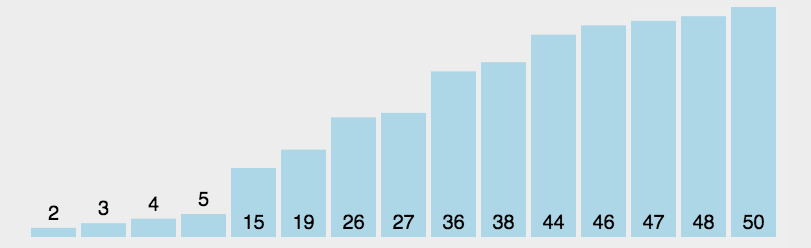
例子里的embedding维度大概是几百,没细数。
将高维嵌入(如文本嵌入)降维到2D(或3D)主要有两个原因:
-
可视化:人类更擅长理解二维或三维的数据,而高维数据往往难以直观理解。通过将高维嵌入降至2D或3D,我们可以直接在平面或空间中可视化数据,比如使用散点图来展示每个数据点。这使我们能够直观地观察数据点之间的相似性和差异性,从而更好地理解数据的分布和结构。
-
计算效率:高维数据通常需要更大的计算资源和存储空间。降维到2D或3D可以减少数据的复杂性,提高计算效率,同时也可以减少存储空间的需求。
值得注意的是,降维过程可能会损失一部分信息。因此,选择合适的降维方法(如PCA、t-SNE等)和降维后的维度是非常重要的,需要根据具体的应用需求和数据特性进行选择。
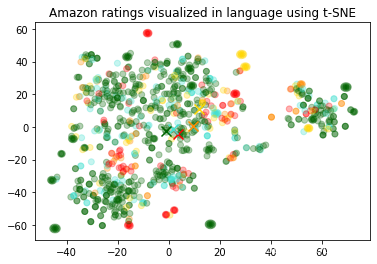
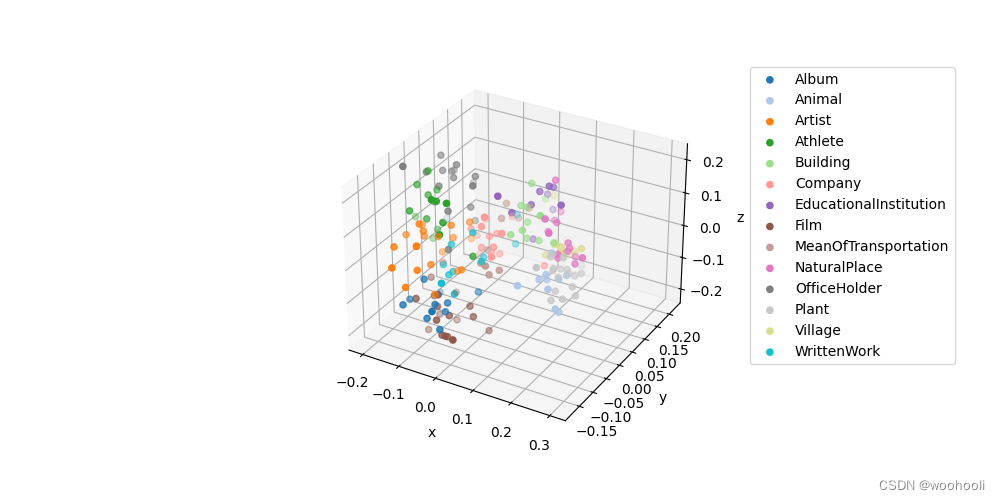
在例子里面有两个数据可视化的代码Visualizing_embeddings_in_3D,Visualizing_embeddings_in_2D,用的分别是PCA和t-SNE.
-
PCA(主成分分析):PCA是一种线性降维技术,它的目标是找到数据的主要特征方向(称为主成分),并用这些方向来表示数据。PCA通过对数据协方差矩阵进行特征分解,找到最大方差的方向作为第一主成分,然后在与之前的主成分正交的方向中找到最大方差的方向作为下一个主成分,以此类推。PCA的一个主要优点是它可以减少数据的噪声,并保留数据的主要特征。但是,PCA是一种线性技术,可能无法很好地处理非线性关系。
-
t-SNE(t-分布式随机邻域嵌入):t-SNE是一种非线性降维技术,特别适合于可视化高维数据集。t-SNE的目标是在低维空间中保持高维空间中的相似度关系。具体来说,t-SNE首先在高维空间中计算每对数据点的相似度,然后在低维空间中尽可能地保持这些相似度。t-SNE的一个主要优点是它可以很好地保持数据的局部结构,能够在低维空间中清晰地展示数据的聚类。但是,t-SNE的计算复杂性较高,可能不适合处理大规模数据集,而且t-SNE的结果可能受初始化和超参数的影响。
这两种方法都有各自的优点和局限性,选择哪种方法取决于具体的应用场景和需求。
例子代码执行后的结果。