🎊专栏【数据结构】
🍔喜欢的诗句:更喜岷山千里雪 三军过后尽开颜。
🎆音乐分享【Dream It Possible】
大一同学小吉,欢迎并且感谢大家指出我的问题🥰
目录
🎁冒泡排序
🏳️🌈图解
🏳️🌈实现过程
🏳️🌈代码
🎁快速排序
🏳️🌈图解
🏳️🌈实现过程
🏳️🌈代码
🎁直接插入排序
🏳️🌈图解
🏳️🌈实现过程
🏳️🌈代码
🎁归并排序
🏳️🌈图解
🏳️🌈实现过程
🏳️🌈代码
🎁选择排序
🏳️🌈图解
🏳️🌈实现过程
🏳️🌈代码
🎁冒泡排序
冒泡排序是一种简单的排序算法,它重复遍历需要排序的数列,每次遍历时比较相邻两个元素的大小,并将它们按照升序或降序的方式进行交换,直到整个数列都排序完成为止。
🏳️🌈图解
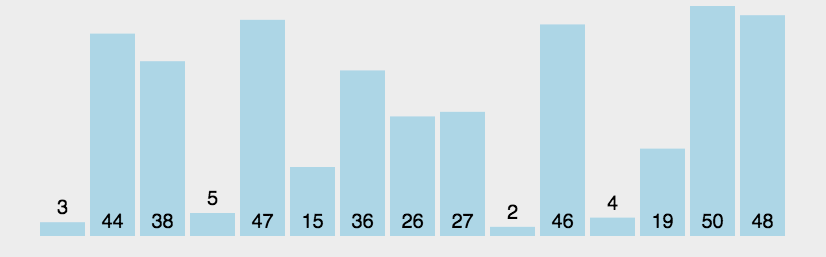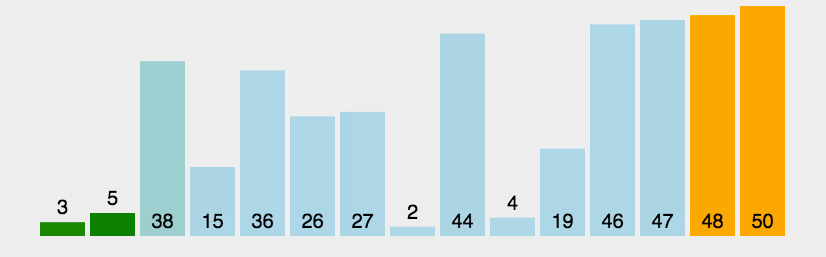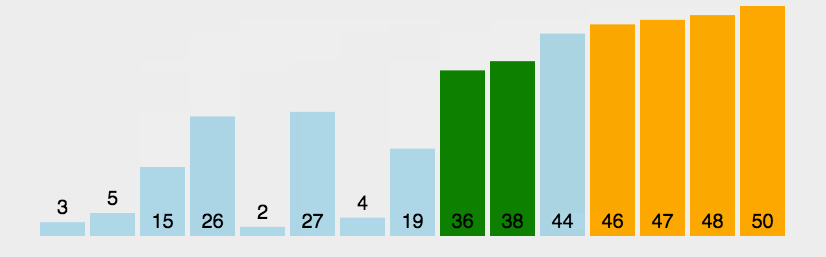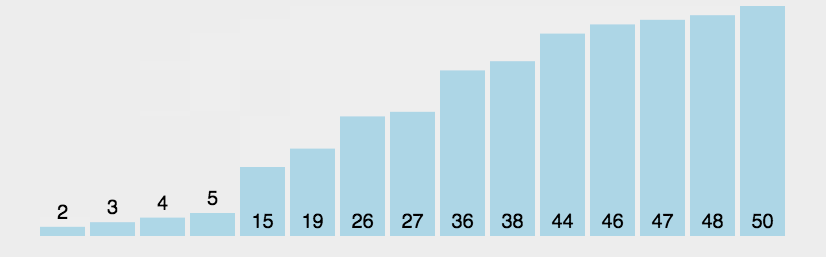
🏳️🌈实现过程
- 从数列的第一个元素开始,对相邻的两个元素进行比较;
- 如果当前元素比后面的元素大(或小,根据排序顺序而定),则交换它们的位置;
- 继续向后遍历,知道全部元素都被遍历完成;
- 重新开始新一轮的遍历操作,但是此时最后一个元素已经不需要再进行比较和交换了,因为已经是最大(或最小)值;
- 重复以上步骤,直到整个数列都被排序完成。
由于每次遍历只能确保一个元素被排序到了正确的位置,因此需要执行多轮的遍历操作才能够保证整个数列都被排序。冒泡排序的时间复杂度为 O(n^2),虽然效率不高,但是实现简单易懂,适用于对较小数列进行排序。
🏳️🌈代码
#include <iostream>
using namespace std;
void bubbleSort(int arr[], int n) {
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// 交换相邻两个元素的值
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
int main() {
int arr[] = {5, 2, 6, 3, 1, 4};
int n = sizeof(arr) / sizeof(arr[0]);
bubbleSort(arr, n);
cout << "排序后的结果为: ";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
return 0;
}
🎁快速排序
快速排序是一种基于“分治法”的排序算法,由C. A. R. Hoare在1960年提出。它通常被认为是最快的通用排序算法之一,并且也是很多编程语言库中的默认排序算法之一。
快速排序的基本思想是:选择一个基准元素(pivot),将待排序的序列分割成两个子序列,其中一个子序列中的所有元素都比基准元素小,另一个子序列中的所有元素都比基准元素大,然后对这两个子序列进行递归排序,直到整个序列有序。
🏳️🌈图解

🏳️🌈实现过程
具体实现过程如下:
- 从数列中选择一个基准元素;
- 将数列中的所有元素分成两个子序列,其中一个子序列中的所有元素都比基准元素小,另一个子序列中的所有元素都比基准元素大;
- 对这两个子序列分别执行递归排序操作,直到整个序列有序。
快速排序的时间复杂度取决于基准元素的选择,最坏情况下的时间复杂度为 O(n^2),但通常情况下时间复杂度为 O(nlogn),并且需要额外的空间来存储递归调用栈。
🏳️🌈代码
#include<iostream>
using namespace std;
int a[100010];
int n;
void quickSort(int a[], int l, int r){
//如果数组中就一个数,就已经排好了,直接返回。
if(l >= r) return;
//选取分界线。这里选数组中间那个数
int x = a[l + r >> 1];
int i = l - 1, j = r + 1;
//划分成左右两个部分
while(i < j){
while(a[++i] < x);
while(a[--j] > x);
if(i < j){
swap(a[i], a[j]);
}
}
//对左部分排序
quickSort(a, l, j);
//对右部分排序
quickSort(a, j + 1, r);
}
int main(){
cin >> n;
for(int i = 0; i < n; i++){
cin >> a[i];
}
quickSort(a, 0, n - 1);
for(int i = 0; i < n; i++){
cout << a[i] << " ";
}
}
🎁直接插入排序
直接插入排序是一种简单的、稳定的排序算法,它的基本思想是将一个待排序的数列看作是由一个有序序列和一个无序序列组成。每次从无序序列中选择一个元素,将其插入到有序序列的适当位置中,从而保证插入后的序列仍然有序。
🏳️🌈图解
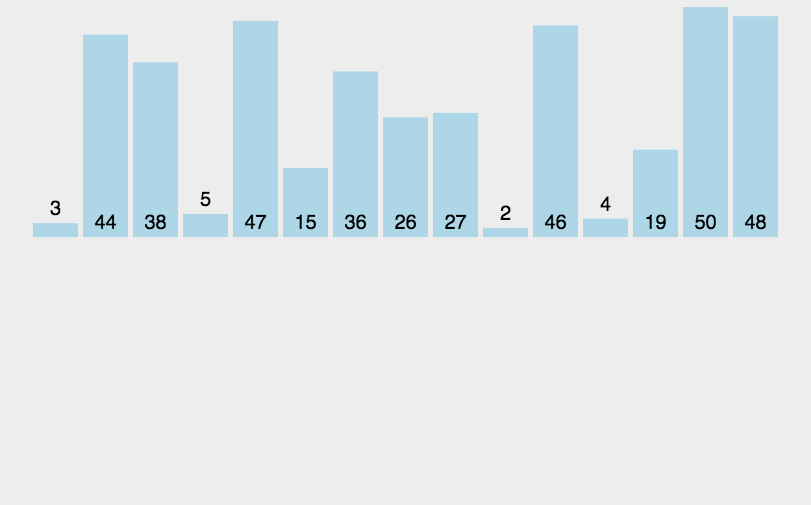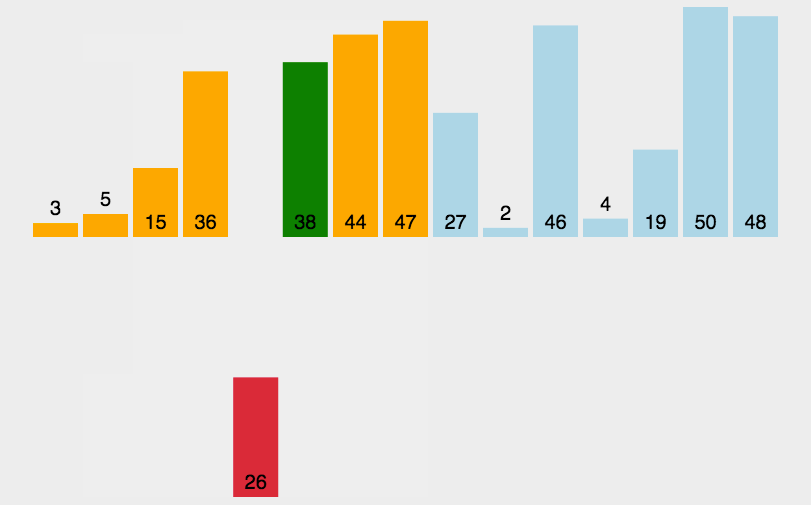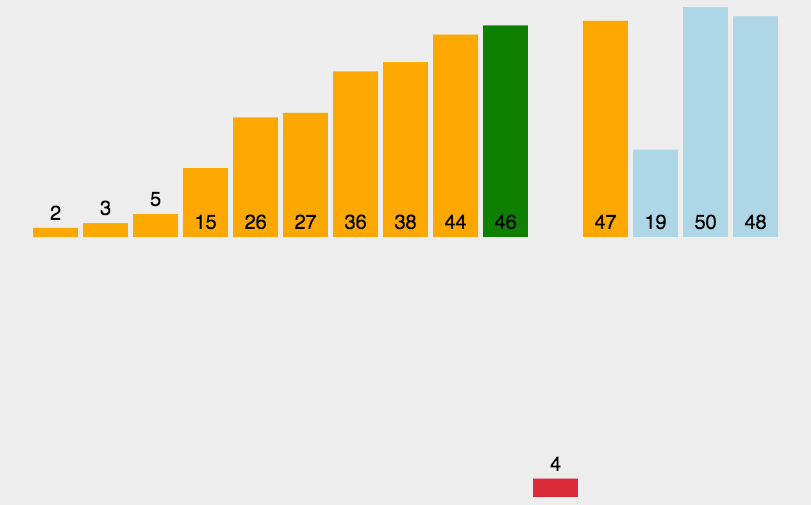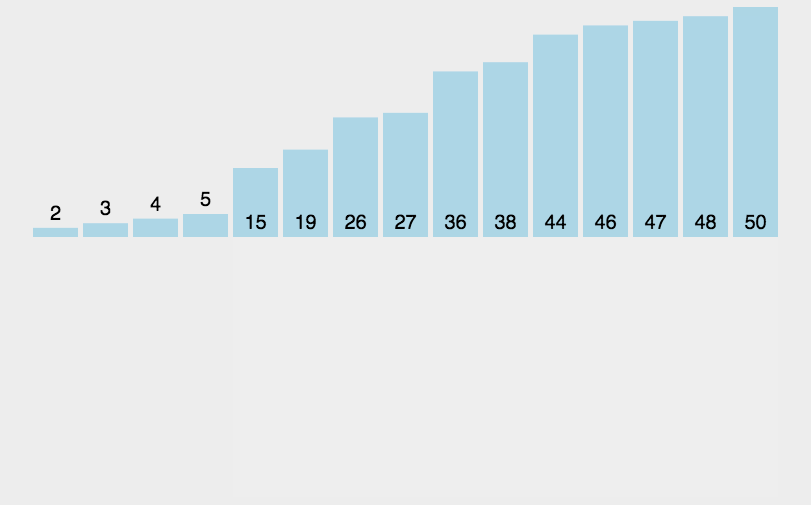
🏳️🌈实现过程
- 将第一个元素看作是一个有序序列;
- 依次将无序序列中的元素插入到有序序列的适当位置中,直到整个序列有序为止;
插入过程中,为了将一个元素插入到有序序列的适当位置中,需要先在有序序列中查找到该元素所应该插入的位置(即需要比较待插入元素与有序序列中已有元素的大小),然后将该元素插入到该位置上,并调整有序序列中的其他元素的位置。插入过程中,需要将待插入元素往后移动,腾出插入位置。
直接插入排序的时间复杂度为 O(n^2),在最坏情况下需要进行 n-1 次比较和移动,但在实际应用中,由于它的操作次数与待排序序列的初始状态有关,因此在部分相对有序的序列中表现良好。
🏳️🌈代码
#include <iostream>
using namespace std;
// 直接插入排序函数
void insertSort(int arr[], int n) {
for (int i = 1; i < n; i++) {
int j = i - 1;
int key = arr[i];
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = key;
}
}
int main() {
int arr[] = {5, 2, 6, 3, 1, 4};
int n = sizeof(arr) / sizeof(arr[0]);
insertSort(arr, n);
cout << "排序后的结果为: ";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
return 0;
}
🎁归并排序
归并排序是一种采用分治策略的排序算法,其基本思想是将一个待排序的数列不断地二分,直到这些子序列都只剩下一个元素。然后再将相邻的子序列两两合并,形成新的有序序列,如此往复,直到最后只剩下一个有序序列为止。
🏳️🌈图解

🏳️🌈实现过程
归并排序的具体实现如下:
- 将待排序的数列不断地二分,直到每个子序列只包含一个元素;
- 将相邻的两个有序子序列合并成一个有序序列;
- 重复第二步操作,直到最后只剩下一个有序序列为止;
在实现中,需要实现一个 merge 函数,用于将两个有序数组合并成一个有序数组。具体操作过程如下:
- 创建一个临时数组 temp,长度等于两个有序数组的长度之和;
- 依次比较两个有序数组中的元素,将较小的元素放入 temp 数组中,直到其中一个数组中的所有元素都被放入为止;
- 将另一个数组中的所有剩余元素依次放入 temp 数组中;
- 将 temp 数组中的元素复制回原数组中。
归并排序的时间复杂度为 O(nlogn),它的性能稳定,并且在处理大规模数据时表现较优。但是它的空间复杂度较高,需要额外的存储空间。
🏳️🌈代码
#include <iostream>
using namespace std;
// 合并两个有序数组
void merge(int arr[], int l, int mid, int r) {
int n1 = mid - l + 1;
int n2 = r - mid;
int L[n1], R[n2];
for (int i = 0; i < n1; i++) {
L[i] = arr[l + i];
}
for (int j = 0; j < n2; j++) {
R[j] = arr[mid + 1 + j];
}
int i = 0, j = 0, k = l;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
k++;
}
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
// 归并排序函数
void mergeSort(int arr[], int l, int r) {
if (l < r) {
int mid = l + (r - l) / 2;
mergeSort(arr, l, mid);
mergeSort(arr, mid + 1, r);
merge(arr, l, mid, r);
}
}
int main() {
int arr[] = {5, 2, 6, 3, 1, 4};
int n = sizeof(arr) / sizeof(arr[0]);
mergeSort(arr, 0, n - 1);
cout << "排序后的结果为: ";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
return 0;
}
🎁选择排序
选择排序是一种简单直观的排序算法,它的基本思想是,每次从待排序的序列中选择一个最小(或最大)的元素,将其放置在已排好序的序列的末尾,直到所有元素都被排序完毕为止。
🏳️🌈图解
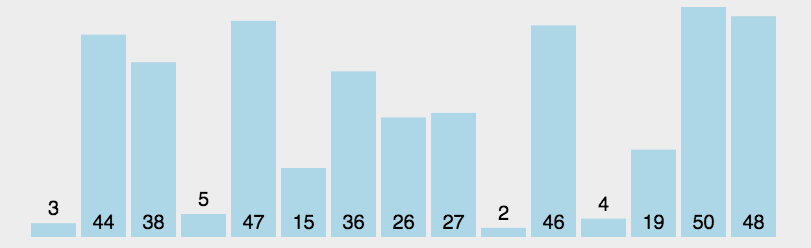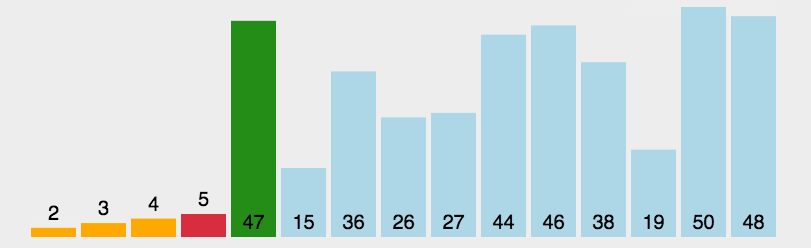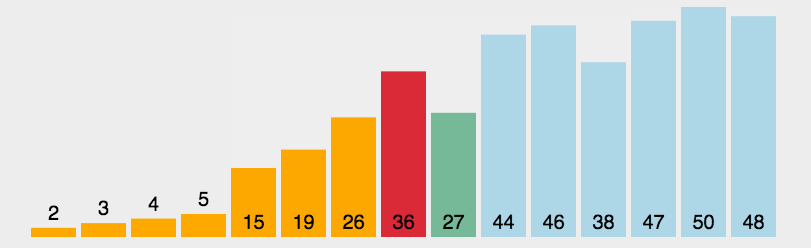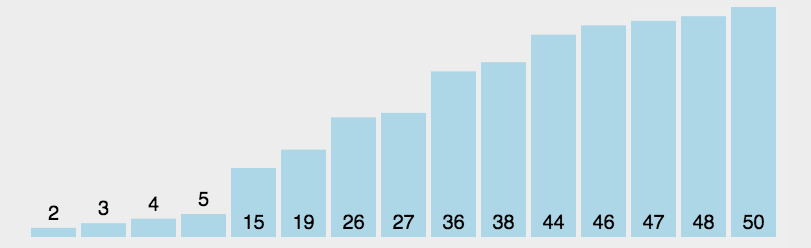
🏳️🌈实现过程
具体实现过程如下:
- 在待排序序列中找到最小元素,并将其放置在序列的起始位置;
- 在剩余未排序的序列中继续寻找最小元素,并将其放置在已排序序列的末尾;
- 重复第二步操作,直到所有元素都被排序完毕。
选择排序的时间复杂度为 O(n^2),且由于其每次只能确定一个元素的位置,因此其性能不够稳定。但是由于其实现简单,空间复杂度低,因此在少量数据的情况下,选择排序仍然具有一定优势。
🏳️🌈代码
#include <iostream>
using namespace std;
void selectionSort(int arr[], int n) {
int minIndex, temp;
for (int i = 0; i < n - 1; i++) {
minIndex = i;
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
}
int main() {
int arr[] = {5, 2, 6, 3, 1, 4};
int n = sizeof(arr) / sizeof(arr[0]);
selectionSort(arr, n);
cout << "排序后的结果为: ";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
return 0;
}
🥰如果大家有不明白的地方,或者文章有问题,欢迎大家在评论区讨论,指正🥰