洛谷——树

文章目录

洛谷——树
- 树的重心
- - 会议
  - - 题目描述
    - 输入格式
    - 输出格式
    - 样例 #1
    - - 样例输入 #1
      - 样例输出 #1
    - 提示
    - - 数据范围
    - 思路
- 树的直径
- - 【XR-3】核心城市
  - - 题目描述
    - 输入格式
    - 输出格式
    - 样例 #1
    - - 样例输入 #1
      - 样例输出 #1
    - 提示
    - 思路
  - [NOI2003] 逃学的小孩
  - - 题目描述
    - 输入格式
    - 输出格式
    - 样例 #1
    - - 样例输入 #1
      - 样例输出 #1
    - 提示
    - 思路
- 最近公共祖先
- - [USACO15DEC]Max Flow P
  - - 题目描述
    - 输入格式
    - 输出格式
    - 样例 #1
    - - 样例输入 #1
      - 样例输出 #1
    - 提示
    - 思路
  - [USACO19DEC]Milk Visits S
  - - 题目描述
    - 输入格式
    - 输出格式
    - 样例 #1
    - - 样例输入 #1
      - 样例输出 #1
    - 提示
    - 思路
  - 仓鼠找 sugar
  - - 题目描述
    - 输入格式
    - 输出格式
    - 样例 #1
    - - 样例输入 #1
      - 样例输出 #1
    - 提示
    - 思路
  - [NOIP2015 提高组] 运输计划
  - - 题目背景
    - 题目描述
    - 输入格式
    - 输出格式
    - 样例 #1
    - - 样例输入 #1
      - 样例输出 #1
    - 提示
    - 思路
- 总结

树的重心

定义：
对于树上的每一个点，计算其所有子树中最大的子树节点数，这个值最小的点就是这棵树的重心。
性质
- 以树的重心为根时，所有子树的大小都不超过整棵树大小的一半。
- 树中所有点到某个点的距离和中，到重心的距离和是最小的；如果有两个重心，那么到它们的距离和一样。
思路
- 首先随便取一个点作为根，自底向下遍历节点，记录包含该节点的子树的节点个数
- 自顶向上遍历节点，记录除了该节点子树节点个数节点的数量
- 最终在所有节点中以上求取的两个最大值中找到最小的那个节点。

会议

题目描述

有一个村庄居住着 $n$ 个村民，有 $n - 1$ 条路径使得这 $n$ 个村民的家联通，每条路径的长度都为 $1$ 。现在村长希望在某个村民家中召开一场会议，村长希望所有村民到会议地点的距离之和最小，那么村长应该要把会议地点设置在哪个村民的家中，并且这个距离总和最小是多少？若有多个节点都满足条件，则选择节点编号最小的那个点。

输入格式

第一行，一个数 $n$ ，表示有 $n$ 个村民。

接下来 $n - 1$ 行，每行两个数字 $a$ 和 $b$ ，表示村民 $a$ 的家和村民 $b$ 的家之间存在一条路径。

输出格式

一行输出两个数字 $x$ 和 $y$ 。

$x$ 表示村长将会在哪个村民家中举办会议。

$y$ 表示距离之和的最小值。

样例 #1

样例输入 #1

样例输出 #1

2 4

提示

数据范围

对于 $70\%$ 数据 $\le 10^3$ 。

对于 $100\%$ 数据 $\le 5 \times 10^4$ 。

思路

本题数据范围要求是一个 $O (n)$ 或者 $O (n l o g n)$ 的复杂度，所以大概只能遍历常数次。而单次遍历得不到所给需求。所以需要在一次遍历中记录相应信息，以待下一次遍历中求出答案。
具体来说，我们首先随便选取一个节点作为根节点。进行一次搜索，在搜索过程中记录每个节点与其子孙间的距离之和。显然这只能得到根节点的距离和。假设 $i$ 节点距离和为 $d [i]$
我们可以思考如果换根后，新根与其子孙的距离和与旧根之间的关系，依据遍历顺序，旧根为新根父亲。
显然可以看做新根距离和，原来子树距离集体减1，旧根距离集体加1.
原来子树集体需要记录为 $sz [i]$ ，相应的旧根集体为 $n - sz [i]$
所以最终答案为 $\times sz[i] + n$

import sys
sys.setrecursionlimit(50010)

def add(a, b) :
	global idx
	e[idx] = b
	ne[idx] = h[a]
	h[a] = idx
	idx += 1

def dfs_d(u, fa) :
	i = h[u]
	while ~ i :
		j = e[i]
		if j != fa :
			dfs_d(j, u)
			sz[u] += sz[j] # 记录以u为根的子树大小
			d[u] += d[j] + sz[j] # 记录子孙节点到节点u的距离和：每上升一层子孙节点到其距离都+1
		i = ne[i]

def dfs_u(u, fa) :
	i = h[u]
	while ~ i :
		j = e[i]
		if j != fa :
			d[j] = d[u] - 2 * sz[j] + n # 求换根后的距离和
			dfs_u(j, u)
		i = ne[i]

n = int(input())
h = [-1] * (n + 7)
ne = [-1] * (2 * n + 7)
e = [0] * (2 * n + 7)
sz = [1] * (n + 7)
d = [0] * (n + 7)
idx = 0

for _ in range(n - 1) :
	a, b = map(int, sys.stdin.readline().split())
	add(a, b)
	add(b, a)

dfs_d(1, -1)
dfs_u(1, -1)
root = 0
res = 1000000010
for i in range(1, n + 1) : # 按序最小
	if res > d[i] :
		root = i
		res = d[i]
print(root, res)

树的直径

定义：树上任意两节点之间最长的简单路径即为树的「直径」。
思路：
定理：在一棵树上，从任意节点 y 开始进行一次 DFS，到达的距离其最远的节点 z 必为直径的一端。
所以先从任意节点 y 开始进行第一次 DFS，到达距离其最远的节点，记为 z，然后再从 z 开始做第二次 DFS，到达距离 z 最远的节点，记为 z’，则 $\delta(z,z')$ 即为树的直径。
树的中心
距离其余节点路径最大值最小的点
做法：换根dp

【XR-3】核心城市

题目描述

X 国有 $n$ 座城市， $n - 1$ 条长度为 $1$ 的道路，每条道路连接两座城市，且任意两座城市都能通过若干条道路相互到达，显然，城市和道路形成了一棵树。

X 国国王决定将 $k$ 座城市钦定为 X 国的核心城市，这 $k$ 座城市需满足以下两个条件：

这 $k$ 座城市可以通过道路，在不经过其他城市的情况下两两相互到达。
定义某个非核心城市与这 $k$ 座核心城市的距离为，这座城市与 $k$ 座核心城市的距离的最小值。那么所有非核心城市中，与核心城市的距离最大的城市，其与核心城市的距离最小。你需要求出这个最小值。

输入格式

第一行 $2$ 个正整数 $n, k$ 。

接下来 $n - 1$ 行，每行 $2$ 个正整数 $u, v$ ，表示第 $u$ 座城市与第 $v$ 座城市之间有一条长度为 $1$ 的道路。

数据范围：

$\le k < n \le 10 ^ 5$ 。
$\le u,v \le n, u \ne v$ ，保证城市与道路形成一棵树。

输出格式

一行一个整数，表示答案。

样例 #1

样例输入 #1

样例输出 #1

提示

【样例说明】

钦定 $1, 2, 5$ 这 $3$ 座城市为核心城市，这样 $3, 4, 6$ 另外 $3$ 座非核心城市与核心城市的距离均为 $1$ ，因此答案为 $1$ 。

思路

首先，对于选取哪个集合作为核心城市是不好考虑的。我们如果考虑单个节点满足其他节点到这个节点的最大值最小，显然这个节点是树的中心。
树的中心一定在核心城市集合里。其他核心城市怎么选取呢？我们需要选取与中心相连且能够使最大值变得最小的点。这里使用了贪心的思想。
如果选取k个节点作为核心城市，除了中心以外的 $k - 1$ 个核心城市，就是分别距离每个节点叶子的最大距离。
这个最大距离可以通过深度来计算。

import sys
from heapq import *
sys.setrecursionlimit(100010)

def add(a, b) :
	global idx
	e[idx] = b
	ne[idx] = h[a]
	h[a] = idx
	idx += 1

def dfs_d(u, fa) : #记录到叶子节点的最大距离和与最大距离不重边的次大距离
	i = h[u]
	while ~ i :
		j = e[i]
		if j != fa :
			dfs_d(j, u)
			if d1[u] <= d1[j] + 1 :
				d1[u], d2[u], s[u] = d1[j] + 1, d1[u], j
			elif d2[u] < d1[j] + 1 :
				d2[u] = d1[j] + 1
		i = ne[i]

def dfs_u(u, fa) : # 记录节点往上路径的最大距离
	i = h[u]
	while ~ i :
		j = e[i]
		if j != fa :
			if s[u] != j :
				up[j] = max(d1[u], up[u]) + 1
			else :
				up[j] = max(d2[u], up[u]) + 1
			dfs_u(j, u)
		i = ne[i]

def dfs(u, fa) : # 处理出节点深度和能往下延伸的最大深度
	i = h[u]
	maxx = 0
	while ~ i :
		j = e[i]
		if j != fa :
			dist[j] = dist[u] + 1
			t = dfs(j, u) # 表示j子树的距离叶子的最大距离
			maxx = max(t, maxx)
		i = ne[i]
	heappush(hq, - (max(dist[u], maxx) - dist[u]))
	return max(dist[u], maxx)

n, m = map(int, input().split())

h = [-1] * (n + 7)
ne = [-1] * (2 * n + 7)
e = [0] * (2 * n + 7)
d1 = [0] * (n + 7)
d2 = [0] * (n + 7)
up = [0] * (n + 7)
s = [0] * (n + 7)
dist = [0] * (n + 7)
hq = []
idx = 0

for _ in range(n - 1) :
	a, b = map(int, sys.stdin.readline().split())
	add(a, b)
	add(b, a)

dfs_d(1, -1)
dfs_u(1, -1)
root = 0
minn = 10000010

for i in range(1, n + 1) : # 找到树的中心
	if max(up[i], d1[i]) < minn :
		minn = max(up[i], d1[i])
		root = i

dfs(root, -1) 
for i in range(m + 1) :
	t = heappop(hq)
	if i == m :
		print(-t + 1)

[NOI2003] 逃学的小孩

题目描述

Chris 家的电话铃响起了，里面传出了 Chris 的老师焦急的声音：“喂，是 Chris 的家长吗？你们的孩子又没来上课，不想参加考试了吗？”一听说要考试，Chris 的父母就心急如焚，他们决定在尽量短的时间内找到 Chris。他们告诉 Chris 的老师：“根据以往的经验，Chris 现在必然躲在朋友 Shermie 或 Yashiro 家里偷玩《拳皇》游戏。现在，我们就从家出发去找 Chris，一但找到，我们立刻给您打电话。”说完砰的一声把电话挂了。

Chris 居住的城市由 $N$ 个居住点和若干条连接居住点的双向街道组成，经过街道 $x$ 需花费 $T_{x}$ 分钟。可以保证，任两个居住点间有且仅有一条通路。Chris 家在点 $C$ ，Shermie 和 Yashiro 分别住在点 $A$ 和点 $B$ 。Chris 的老师和 Chris 的父母都有城市地图，但 Chris 的父母知道点 $A$ 、 $B$ 、 $C$ 的具体位置而 Chris 的老师不知。

为了尽快找到 Chris，Chris 的父母会遵守以下两条规则：

如果 $A$ 距离 $C$ 比 $B$ 距离 $C$ 近，那么 Chris 的父母先去 Shermie 家寻找 Chris，如果找不到，Chris 的父母再去 Yashiro 家；反之亦然。
Chris 的父母总沿着两点间唯一的通路行走。

显然，Chris 的老师知道 Chris 的父母在寻找 Chris 的过程中会遵守以上两条规则，但由于他并不知道 $A$ 、 $B$ 、 $C$ 的具体位置，所以现在他希望你告诉他，最坏情况下 Chris的父母要耗费多长时间才能找到 Chris？

输入格式

输入文件第一行是两个整数 $N$ 和 $M$ ，分别表示居住点总数和街道总数。

以下 $M$ 行，每行给出一条街道的信息。第 $i + 1$ 行包含整数 $U_{i}$ 、 $V_{i}$ 、 $T_{i}$ ，表示街道 $i$ 连接居住点 $U_{i}$ 和 $V_{i}$ ，并且经过街道 $i$ 需花费 $T_{i}$ 分钟。街道信息不会重复给出。

输出格式

输出文件仅包含整数 $T$ ，即最坏情况下 Chris 的父母需要花费 $T$ 分钟才能找到 Chris。

样例 #1

样例输入 #1

样例输出 #1

提示

对于 $100\%$ 的数据， $\le N \le 2\times 10^5$ ， $\le U_{i},V_{i} \le N$ ， $\le T_{i} \le 10^{9}$ 。

思路

要求在树上找到三个点，要求 $ma x (min (A C, BC) + A B)$ 。在一棵树上，从任意节点 y 开始进行一次 DFS，到达的距离其最远的节点 z 必为直径的一端。所以 $A B$ 一定是直径， $C$ 选取距离端点最近距离最远的点即可。

import sys
sys.setrecursionlimit(200010)
tmp = 0
def add(a, b, c) :
	global idx
	e[idx] = b
	w[idx] = c
	ne[idx] = h[a]
	h[a] = idx
	idx += 1

def dfs(u, fa) : # 求以u为根的到根最大距离，并返回最大距离对应的点
    global tmp
    i = h[u]
    while ~ i :
        j = e[i]
        if j != fa :
            d[j] = d[u] + w[i]
            if d[j] > d[tmp] :
                tmp = j
            dfs(j, u)
        i = ne[i]
	

n, m = map(int, input().split())

h = [-1] * (n + 7)
ne = [-1] * (2 * n + 7)
e = [0] * (2 * n + 7)
w = [0] * (2 * n + 7)
d = [0] * (n + 7)
tmp = 0
idx = 0

for _ in range(m) :
	a, b, c = map(int, input().split())
	add(a, b, c)
	add(b, a, c)

dfs(1, -1)
A = tmp
tmp = 1
d = [0] * (n + 7)
dfs(A, -1)
B = tmp
d1 = d[:]
d = [0] * (n + 7)
dfs(B, -1)
d2 = d[:]
maxx = d1[B]
for i in range(1, n + 1) :
	maxx = max(maxx, d1[B] + min(d1[i], d2[i]))
print(maxx)

最近公共祖先

定义：最近公共祖先简称 LCA（Lowest Common Ancestor）。两个节点的最近公共祖先，就是这两个点的公共祖先里面，离根最远的那个。为了方便，我们记某点集 $S=\{v_1,v_2,\ldots,v_n\}$ 的最近公共祖先为 $\text{LCA}(v_1,v_2,\ldots,v_n) 或 \text{LCA}(S)$ 。
应用：树上路径(两点间的距离)，树上差分（记录路径上的点或边通过数）

[USACO15DEC]Max Flow P

题目描述

Farmer John has installed a new system of $N - 1$ pipes to transport milk between the $N$ stalls in his barn ( $\leq N \leq 50,000$ ), conveniently numbered $\ldots N$ . Each pipe connects a pair of stalls, and all stalls are connected to each-other via paths of pipes.

FJ is pumping milk between $K$ pairs of stalls ( $\leq K \leq 100,000$ ). For the $i$ th such pair, you are told two stalls $s_i$ and $t_i$ , endpoints of a path along which milk is being pumped at a unit rate. FJ is concerned that some stalls might end up overwhelmed with all the milk being pumped through them, since a stall can serve as a waypoint along many of the $K$ paths along which milk is being pumped. Please help him determine the maximum amount of milk being pumped through any stall. If milk is being pumped along a path from $s_i$ to $t_i$ , then it counts as being pumped through the endpoint stalls $s_i$ and

$t_i$ , as well as through every stall along the path between them.

FJ 给他的牛棚的 $N$ 个隔间之间安装了 $N - 1$ 根管道，隔间编号从 $1$ 到 $N$ 。所有隔间都被管道连通了。

FJ 有 $K$ 条运输牛奶的路线，第 $i$ 条路线从隔间 $s_i$ 运输到隔间 $t_i$ 。一条运输路线会给它的两个端点处的隔间以及中间途径的所有隔间带来一个单位的运输压力，你需要计算压力最大的隔间的压力是多少。

输入格式

The first line of the input contains $N$ and $K$ .

The next $N - 1$ lines each contain two integers $x$ and $y$ ( $\ne y$ ) describing a pipe

between stalls $x$ and $y$ .

The next $K$ lines each contain two integers $s$ and $t$ describing the endpoint

stalls of a path through which milk is being pumped.

第一行输入两个整数 $N$ 和 $K$ 。

接下来 $N - 1$ 行每行输入两个整数 $x$ 和 $y$ ，其中 $\ne y$ 。表示一根在牛棚 $x$ 和 $y$ 之间的管道。

接下来 $K$ 行每行两个整数 $s$ 和 $t$ ，描述一条从 $s$ 到 $t$ 的运输牛奶的路线。

输出格式

An integer specifying the maximum amount of milk pumped through any stall in the barn.

一个整数，表示压力最大的隔间的压力是多少。

样例 #1

样例输入 #1

样例输出 #1

提示

$\le N \le 5 \times 10^4,1 \le K \le 10^5$

思路

第 $i$ 条路线从隔间 $s_i$ 运输到隔间 $t_i$ 。一条运输路线会给它的两个端点处的隔间以及中间途径的所有隔间带来一个单位的运输压力。也就是给定两个结点，让这个路径上的每个点的权值都加1，因此可以用树上差分。这是一个对于点上的差分。假设两个结点为 $a ， b$ ，定义 $d [i]$ 为经过 $i$ 结点的差分数组。则让这个路径上的每个点的权值都加1，即为 $d [a] + = 1, d [b] + = 1, d [l c a (a, b)] - = 1, d [f [l c a (a, b) [0]]] - = 1$ ,最终求取一条节点的通过数。

import sys
from math import log
from collections import deque
sys.setrecursionlimit(50010)

def add(a, b) :
	global idx
	e[idx] = b
	ne[idx] = h[a]
	h[a] = idx
	idx += 1

def bfs(u) : # 求深度+预处理f
	que = deque()
	que.appendleft(u)
	d[u] = 0
	while len(que) :
		t = que.pop()
		i = h[t]
		while ~ i :
			j = e[i]
			if d[j] == -1 :
				d[j] = d[t] + 1
				que.appendleft(j)
				f[j][0] = t
				for k in range(1, length + 1) :
					f[j][k] = f[f[j][k - 1]][k - 1]
			i = ne[i]

def lca(a, b) : 
	if d[a] < d[b] :
		a, b = b, a
	for i in range(length, -1, -1) :
		if d[f[a][i]] >= d[b] :
			a = f[a][i]
	if a == b :
		return a
	for i in range(length, -1, -1) :
		if f[a][i] != f[b][i] :
			a, b = f[a][i], f[b][i]
	return f[a][0]

def dfs(u, fa) : # 求路径前缀和
	global ans
	i = h[u]
	while ~ i :
		j = e[i]
		if j != fa :
			dfs(j, u)
			dif[u] += dif[j]
		i = ne[i]
	ans = max(dif[u], ans)
	

n, m = map(int, input().split())
h = [-1] * (n + 7)
e = [0] * (2 * n + 7)
ne = [-1] * (2 * n + 7)
dif = [0] * (n + 7)
d = [-1] * (n + 7)
f = [[0] * 20 for _ in range(n + 7)]
idx = 0
length = int(log(n, 2)) + 1

for _ in range(n - 1) :
	a, b = map(int, sys.stdin.readline().split())
	add(a, b)
	add(b, a)

bfs(1)

for _ in range(m) :
	a, b = map(int, sys.stdin.readline().split())
	fa = lca(a, b)
	dif[a] += 1
	dif[b] += 1
	dif[fa] -= 1
	dif[f[fa][0]] -= 1
ans = 0
dfs(1, -1)
print(ans)

[USACO19DEC]Milk Visits S

题目描述

Farmer John 计划建造 $N$ 个农场，用 $N - 1$ 条道路连接，构成一棵树（也就是说，所有农场之间都互相可以到达，并且没有环）。每个农场有一头奶牛，品种为更赛牛或荷斯坦牛之一。

Farmer John 的 $M$ 个朋友经常前来拜访他。在朋友 $i$ 拜访之时，Farmer John 会与他的朋友沿着从农场 $A_i$ 到农场 $B_i$ 之间的唯一路径行走（可能有 $A_i = B_i$ ）。除此之外，他们还可以品尝他们经过的路径上任意一头奶牛的牛奶。由于 Farmer John 的朋友们大多数也是农场主，他们对牛奶有着极强的偏好。他的有些朋友只喝更赛牛的牛奶，其余的只喝荷斯坦牛的牛奶。任何 Farmer John 的朋友只有在他们访问时能喝到他们偏好的牛奶才会高兴。

请求出每个朋友在拜访过后是否会高兴。

输入格式

输入的第一行包含两个整数 $N$ 和 $M$ 。

第二行包含一个长为 $N$ 的字符串。如果第 $i$ 个农场中的奶牛是更赛牛，则字符串中第 $i$ 个字符为 G，如果第 $i$ 个农场中的奶牛是荷斯坦牛则为 H。

以下 $N - 1$ 行，每行包含两个不同的整数 $X$ 和 $Y$ （ $\leq X, Y \leq N$ ），表示农场 $X$ 与 $Y$ 之间有一条道路。

以下 $M$ 行，每行包含整数 $A_i$ ， $B_i$ ，以及一个字符 $C_i$ 。 $A_i$ 和 $B_i$ 表示朋友 $i$ 拜访时行走的路径的端点， $C_i$ 是 G 或 H 之一，表示第 $i$ 个朋友喜欢更赛牛的牛奶或是荷斯坦牛的牛奶。

输出格式

输出一个长为 $M$ 的二进制字符串。如果第 $i$ 个朋友会感到高兴，则字符串的第 $i$ 个字符为 1，否则为 0。

样例 #1

样例输入 #1

样例输出 #1

提示

在这里，从农场 1 到农场 4 的路径包括农场 1、2 和 4。所有这些农场里都是荷斯坦牛，所以第一个朋友会感到满意，而第二个朋友不会。

关于部分分：

测试点 $1$ 样例。

测试点 $2\sim 5$ 满足 $N\le 10^3$ ， $M\le 2\cdot 10^3$ 。

对于 $100\%$ 的数据， $\leq N \leq 10^5$ ， $\leq M \leq 10^5$ 。

供题：Spencer Compton

思路

求两点之间路径是否存在某个性质的点， $l c a$ 扩展。
lca+状态判断
f[i, k, 0]表示正常意义
f[i, k, 1]表示路径上是否有H牛
f[i, k, 2]表示路径上是否有G牛

'''
lca+状态判断
f[i, k, 0]表示正常意义
f[i, k, 1]表示路径上是否有H牛
f[i, k, 2]表示路径上是否有G牛
'''
import sys
from math import log
from collections import deque
sys.setrecursionlimit(1010)

def add(a, b) :
    global idx
    e[idx] = b
    ne[idx] = h[a]
    h[a] = idx
    idx += 1

def bfs(u) :
    que = deque()
    que.appendleft(u)
    d[u] = 0
    while len(que) :
        t = que.pop()
        i = h[t]
        while ~ i :
            j = e[i]
            if d[j] == -1 :
                d[j] = d[t] + 1
                f[j][0][0] = t
                f[j][0][1] = s[j - 1] == 'H' or s[t - 1] == 'H'
                f[j][0][2] = s[j - 1] == 'G' or s[t - 1] == 'G'
                que.appendleft(j)
                for k in range(1, length + 1) :
                    f[j][k][0] = f[f[j][k - 1][0]][k - 1][0]
                    f[j][k][1] = f[j][k - 1][1] or f[f[j][k - 1][0]][k - 1][1]
                    f[j][k][2] = f[j][k - 1][2] or f[f[j][k - 1][0]][k - 1][2]
            i = ne[i]

def lca(a, b, c) :
    if d[a] < d[b] :
        a, b = b, a
    for i in range(length, -1, -1) :
        if d[f[a][i][0]] >= d[b] :
            if f[a][i][c] :
                return 1
            a = f[a][i][0]
    if a == b :
        if c == 1 :
            if s[a - 1] == "H" :
                return 1
        else :
            if s[a - 1] == "G" :
                return 1
        return 0
    for i in range(length, -1, -1) :
        if f[a][i][0] != f[b][i][0] :
            if f[a][i][c] or f[b][i][c] :
                return 1
            a, b = f[a][i][0], f[b][i][0]
    if f[a][0][c] or f[b][0][c] : return 1
    return 0

n, m = map(int, input().split())

s = input()
h = [-1] * (n + 7)
e = [0] * (2 * n + 7)
ne = [-1] * (2 * n + 7)
d = [-1] * (n + 7)
f = [[[0, 0, 0] for _ in range(20)] for _ in range(n + 7)]
idx = 0
length = int(log(n, 2)) + 1

for _ in range(n - 1) :
    a, b = map(int, sys.stdin.readline().split())
    add(a, b)
    add(b, a)

bfs(1)

res = ''
for _ in range(m) :
    a, b, c = sys.stdin.readline().split()
    a, b = int(a), int(b)
    if c == 'H' :
        res += str(int(lca(a, b, 1)))
    else :
        res += str(int(lca(a, b, 2)))
print(res)

仓鼠找 sugar

题目描述

小仓鼠的和他的基（mei）友（zi）sugar住在地下洞穴中，每个节点的编号为1~n。地下洞穴是一个树形结构。这一天小仓鼠打算从从他的卧室（a）到餐厅（b），而他的基友同时要从他的卧室（c）到图书馆（d）。他们都会走最短路径。现在小仓鼠希望知道，有没有可能在某个地方，可以碰到他的基友？

小仓鼠那么弱，还要天天被zzq大爷虐，请你快来救救他吧！

输入格式

第一行两个正整数n和q，表示这棵树节点的个数和询问的个数。

接下来n-1行，每行两个正整数u和v，表示节点u到节点v之间有一条边。

接下来q行，每行四个正整数a、b、c和d，表示节点编号，也就是一次询问，其意义如上。

输出格式

对于每个询问，如果有公共点，输出大写字母“Y”；否则输出“N”。

样例 #1

样例输入 #1

样例输出 #1

Y
N
Y
Y
Y

提示

__本题时限1s，内存限制128M，因新评测机速度较为接近NOIP评测机速度，请注意常数问题带来的影响。__

20%的数据 n<=200,q<=200

40%的数据 n<=2000,q<=2000

70%的数据 n<=50000,q<=50000

100%的数据 n<=100000,q<=100000

思路

判断两个路径是否有相交等价于只要存在其中一个两个端点的 $l c a$ 在另一条路径上即可。
如何判断一个节点是否在一条路径上呢？
只需要满足，这个节点 $x$ 比路径两端 $A, B$ 的公共祖先 $f a$ 的深度小，且满足 $l c a (A, x) = x or l c a (B, x) = x$

'''
如果树上两个路径相交，则其中一个路径两端的lca一定在另一条路径上
判断lca x在路径s~t上(if d[s] > d[t])
则lca(s, x) = x and lca(x, t) = t 
'''
import sys
from math import log
from collections import deque
sys.setrecursionlimit(100010)

def add(a, b) :
    global idx
    e[idx] = b
    ne[idx] = h[a]
    h[a] = idx
    idx += 1

def bfs(u) :
    que = deque()
    que.appendleft(u)
    dist[u] = 0
    while len(que) :
        t = que.pop()
        i = h[t]
        while ~ i :
            j = e[i]
            if dist[j] == -1 :
                dist[j] = dist[t] + 1
                que.appendleft(j)
                f[j][0] = t
                for k in range(1, length + 1) :
                    f[j][k] = f[f[j][k - 1]][k - 1]
            i = ne[i]

def lca(a, b) :
    if dist[a] < dist[b] :
        a, b = b, a
    for i in range(length, -1, -1) :
        if dist[f[a][i]] >= dist[b] :
            a = f[a][i]
    if a == b :
        return a
    for i in range(length, -1, -1) :
        if f[a][i] != f[b][i] :
            a, b = f[a][i], f[b][i]
    return f[a][0]

n, m = map(int, input().split())
h = [-1] * (n + 7)
e = [0] * (2 * n + 7)
ne = [-1] * (2 * n + 7)
idx = 0
length = int(log(n, 2)) + 1
f = [[0] * (20) for _ in range(n + 7)]
dist = [-1] * (n + 7)

for _ in range(n  - 1) :
    a, b = map(int, sys.stdin.readline().split())
    add(a, b)
    add(b, a)

bfs(1)
# print(dist)

for _ in range(m) :
    flag = True
    a, b, c, d = map(int, sys.stdin.readline().split())
    x, y = lca(a, b), lca(c, d)
    # print(x, y)
    if dist[x] >= dist[y] :
        if lca(c, x) == x or lca(d, x) == x :
            flag = False
    else :
        if lca(a, y) == y or lca(b, y) == y :
            flag = False
    if not flag :
        print("Y")
    else :
        print("N")

[NOIP2015 提高组] 运输计划

题目背景

公元 $2044$ 年，人类进入了宇宙纪元。

题目描述

公元 $2044$ 年，人类进入了宇宙纪元。

L 国有 $n$ 个星球，还有 $n - 1$ 条双向航道，每条航道建立在两个星球之间，这 $n - 1$ 条航道连通了 L 国的所有星球。

小 P 掌管一家物流公司，该公司有很多个运输计划，每个运输计划形如：有一艘物流飞船需要从 $u_i$ 号星球沿最快的宇航路径飞行到 $v_i$ 号星球去。显然，飞船驶过一条航道是需要时间的，对于航道 $j$ ，任意飞船驶过它所花费的时间为 $t_j$ ，并且任意两艘飞船之间不会产生任何干扰。

为了鼓励科技创新， L 国国王同意小 P 的物流公司参与 L 国的航道建设，即允许小 P 把某一条航道改造成虫洞，飞船驶过虫洞不消耗时间。

在虫洞的建设完成前小 P 的物流公司就预接了 $m$ 个运输计划。在虫洞建设完成后，这 $m$ 个运输计划会同时开始，所有飞船一起出发。当这 $m$ 个运输计划都完成时，小 P 的物流公司的阶段性工作就完成了。

如果小 P 可以自由选择将哪一条航道改造成虫洞，试求出小 P 的物流公司完成阶段性工作所需要的最短时间是多少？

输入格式

第一行包括两个正整数 $n, m$ ，表示 L 国中星球的数量及小 P 公司预接的运输计划的数量，星球从 $1$ 到 $n$ 编号。

接下来 $n - 1$ 行描述航道的建设情况，其中第 $i$ 行包含三个整数 $a_i, b_i$ 和 $t_i$ ，表示第 $i$ 条双向航道修建在 $a_i$ 与 $b_i$ 两个星球之间，任意飞船驶过它所花费的时间为 $t_i$ 。

数据保证

接下来 $m$ 行描述运输计划的情况，其中第 $j$ 行包含两个正整数 $u_j$ 和 $v_j$ ，表示第 $j$ 个运输计划是从 $u_j$ 号星球飞往 $v_j$ 号星球。

输出格式

一个整数，表示小 P 的物流公司完成阶段性工作所需要的最短时间。

样例 #1

样例输入 #1

样例输出 #1

提示

所有测试数据的范围和特点如下表所示

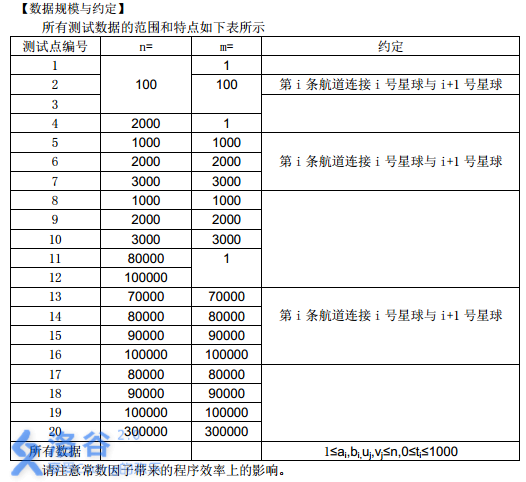
请注意常数因子带来的程序效率上的影响。

对于 $100\%$ 的数据，保证： $\leq a_i,b_i \leq n$ ， $\leq t_i \leq 1000$ ， $\leq u_i,v_i \leq n$ 。

思路

对于最小最大值问题，可以通过右半段二分答案，找到可以覆盖所有减去一条边后的路径。
假设二分答案是 $x$ ，如何检测是否可以满足条件呢？
我们分两步走：

首先统计出所有大于 $x$ 的路径及其数量，并记录这些路径上的边的通过数
其次找到这些路径的公共边中通过数刚好等于路径数的，并检测所有这些路径中的最大值减去这个边后是否小于 $x$

对于其中的细节问题：
对于路径长度可以通过 $l c a$ 计算，假设 $d [i]$ 表示 $i$ 节点的深度，则 $a, b$ 两节点的路径长度为 $\times d[lca(a, b)]$
对于路径上边的通过数，用树上差分统计。
如果通过一次 $a, b$ 为端点的路径，设 $d i f [i]$ 表示 $i$ 入度的路径通过数的差分数组，是与子节点的差值。则通过一次的操作，记录为 $d i f [a] + = 1, d i f [b] + 1, d i f [l c a (a, b)] - = 2$ ,注意与记录点的差别。
如果想统计每条边的通过数，则进行一遍 $df s$ 求和即可。

import sys
from math import log
from collections import deque

def add(a, b, c) :
    global idx
    e[idx] = b
    w[idx] = c
    ne[idx] = h[a]
    h[a] = idx
    idx += 1

def bfs(u) :
    que = deque()
    que.appendleft(u)
    d[u], dist[u] = 0, 0
    while len(que) :
        t = que.pop()
        i = h[t]
        while ~ i :
            j = e[i]
            if d[j] == -1 :
                d[j] = d[t] + 1
                dist[j] = dist[t] + w[i]
                f[j][0] = t
                que.appendleft(j)
                for k in range(1, length + 1) :
                    f[j][k] = f[f[j][k - 1]][k - 1]
            i = ne[i]

def lca(a, b) :
    if d[a] < d[b] :
        a, b = b, a
    for i in range(length, -1, -1) :
        if d[f[a][i]] >= d[b] :
            a = f[a][i]
    if a == b :
        return a
    for i in range(length, -1, -1) :
        if f[a][i] != f[b][i] :
            a, b = f[a][i], f[b][i]
    return f[a][0]

def dfs(u, fa) :
    i = h[u]
    while ~ i :
        j = e[i]
        if j != fa :
            dfs(j, u)
            s[u] += s[j]
        i = ne[i]

def check(x) :
    global s
    cnt = 0
    maxx = 0
    s = [0] * (n + 7)
    num = []
    for i in range(m) :
        a, b, fa, distant = q[i] 
        if distant > x :
            cnt += 1
            maxx = max(maxx, distant - x)
            s[a] += 1
            s[b] += 1
            s[fa] -= 2
            num.append(i)
    if cnt == 0 :
        return True
    # 求前缀和
    dfs(1, -1)
    for i in range(1, n + 1) :
        if s[i] == cnt :
            if dist[i] - dist[f[i][0]] >= maxx :
                return True
    return False

    

sys.setrecursionlimit(300010)
n, m = map(int, input().split())

h = [-1] * (n + 7)
ne = [-1] * (2 * n + 7)
e = [0] * (2 * n + 7)
w = [0] * (2 * n + 7)
q = []
d = [-1] * (n + 7)
dist = [0] * (n + 7)
f = [[0] * 20 for _ in range(n + 7)]
s = [0] * (n + 7)
idx = 0
length = int(log(n, 2)) + 1

for _ in range(n - 1) :
    a, b, c = map(int, sys.stdin.readline().split())
    add(a, b, c)
    add(b, a, c)

bfs(1)

r = 0
for _ in range(m) :
    a, b = map(int, sys.stdin.readline().split())
    fa = lca(a, b)
    tmp = dist[a] + dist[b] - 2 * dist[fa]
    # print(dist[a], dist[b], dist[fa], tmp)
    q.append([a, b, fa, tmp])
    r += tmp

l = 0

while l < r : # 二分答案
    mid = (l + r) >> 1
    if check(mid) :
        r = mid
    else :
        l = mid + 1
print(l)