栈的介绍

栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。
压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。
出栈：栈的删除操作叫做出栈。出数据也在栈顶。

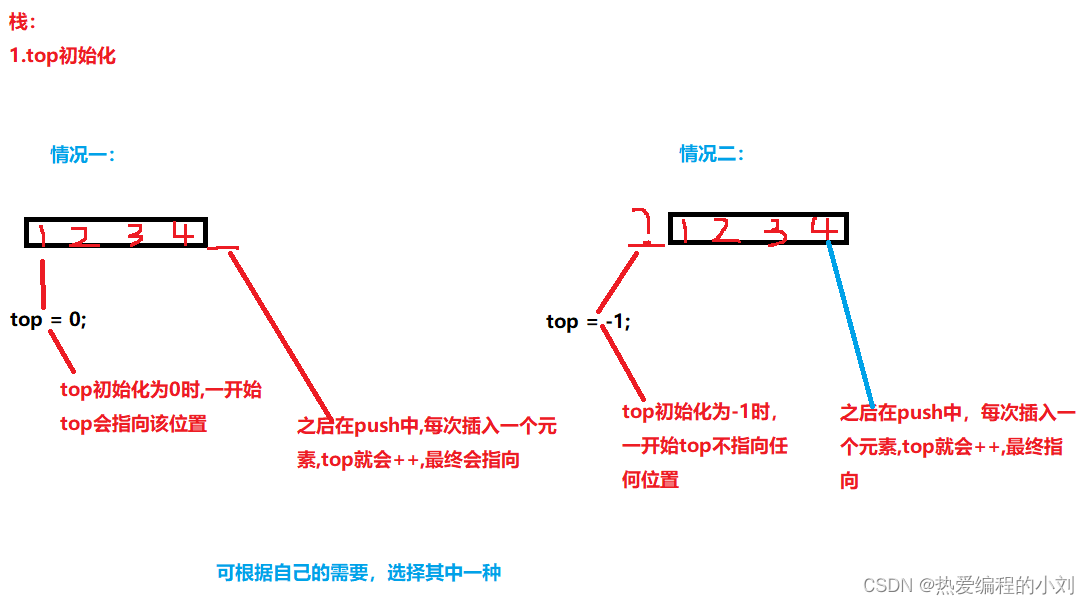
栈的初始化

//.h头文件内
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>
//数组类型栈
typedef int STDataType;
typedef struct Stack
{
	STDataType* a;
	int top;//栈顶
	int capacity;//容量
}Stack;
// 初始化栈 
void StackInit(Stack* ps);

//.c逻辑文件


// 初始化栈 
void StackInit(Stack* ps)
{
	assert(ps);
	ps->a = NULL;
	//ps->top = -1;//top栈顶初始化为-1最后会指向栈顶元素
	ps->top = 0;//top栈顶初始化为0最后会指向栈顶元素的下一个位置
	ps->capacity = 0;
}

栈的插入(入栈)

//.h头文件
// 入栈 
void StackPush(Stack* ps, STDataType data);

//.c逻辑文件
// 入栈 
void StackPush(Stack* ps, STDataType data)
{
	assert(ps);
	if (ps->capacity == ps->top)
	{
		int num = ps->capacity == 0 ? 4 : ps->capacity * 2;
		STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * num);
		if (tmp == NULL)
		{
			perror("realloc fail:");
			return;
		}
		ps->a = tmp;
		ps->capacity = num;
	}
	ps->a[ps->top] = data;
	ps->top++;
}

栈的出栈

//.h文件
// 出栈 
void StackPop(Stack* ps);

//.c逻辑文件
// 出栈 
void StackPop(Stack* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));
	ps->top--;
}

获取栈顶元素

//.h头文件
// 获取栈顶元素 
STDataType StackTop(Stack* ps);

//.c逻辑文件
// 获取栈顶元素 
STDataType StackTop(Stack* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));
	return ps->a[ps->top - 1];
}

获取栈中有效元素个数

//.h头文件
// 获取栈中有效元素个数 
int StackSize(Stack* ps);

//.c逻辑文件
// 获取栈中有效元素个数 
int StackSize(Stack* ps)
{
	assert(ps);
	return ps->top;
}

检测栈是否为空

//.h头文件
// 检测栈是否为空，如果为空返回false，如果不为空true
bool StackEmpty(Stack* ps);

//.c逻辑文件
// 检测栈是否为空，如果为空返回非零结果，如果不为空返回0 
bool StackEmpty(Stack* ps)
{
	assert(ps);
	return ps->top == 0;
}

销毁栈

//.h头文件
// 销毁栈 
void StackDestroy(Stack* ps);

//.c逻辑文件
// 销毁栈 
void StackDestroy(Stack* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->capacity = ps->top = 0;
}

栈元素打印

想打印栈内元素,不能跟顺序表与链表一样定义打印函数,因为栈规定“先进后出”原则,因此想打印栈内元素,我们要在测试文件中打印

#define _CRT_SECURE_NO_WARNINGS 1
#include"Stack.h"
void test1()
{
	Stack ps;
	// 初始化栈 
	StackInit(&ps);
	StackPush(&ps,1);
	StackPush(&ps,2);
	StackPop(&ps);
	StackPush(&ps,3);
	StackPush(&ps,4);
	int num = StackSize(&ps);
	printf("%d\n", num);
	//打印栈（栈的打印与顺序表链表不同,不能定义一个专门用于打印的函数，因为栈要遵循先进后出原则）
	while (!StackEmpty(&ps))
	{
		printf("%d ", StackTop(&ps));
		StackPop(&ps);
	}
	// 销毁栈 
	StackDestroy(&ps);
}
int main()
{
	test1();
	return 0;
}