目录
1、选择排序
1.1、算法思想
1.2、步骤
1.3、算法实现
1.4、算法分析
2、 冒泡排序
2.1、算法思想
2.2、算法实现
2.3、算法分析
2.4、改进冒泡排序
3、插入排序
3.1、算法思想
3.2、算法实现
3.3、算法分析
4、希尔排序
4.1、算法思想
4.2、增长量选定规则
4.3、算法实现
4.4、算法分析
5、归并排序
5.1、算法思想
5.2、算法实现
5.3、算法分析
6、快速排序
6.1、算法思想
6.2、算法实现
6.3、算法分析
7、基数排序(桶排序)
7.1、算法思想
7.2、算法步骤
7.3、算法实现
7.4、算法分析
8、堆积树排序
8.1、算法思想
1、选择排序
1.1、算法思想
每趟从待排序的数据元素中,选出最小(或最大)的一个元素,顺序放在待排序的数列最前面,直到全部待排序的数据元素排完。
1.2、步骤
1、查找此数列中的最小元素,将其与第一个交换
2、从第二个值开始找,查找到最小元素,将其与第二个交换
3、以此类推,直到遍历结束
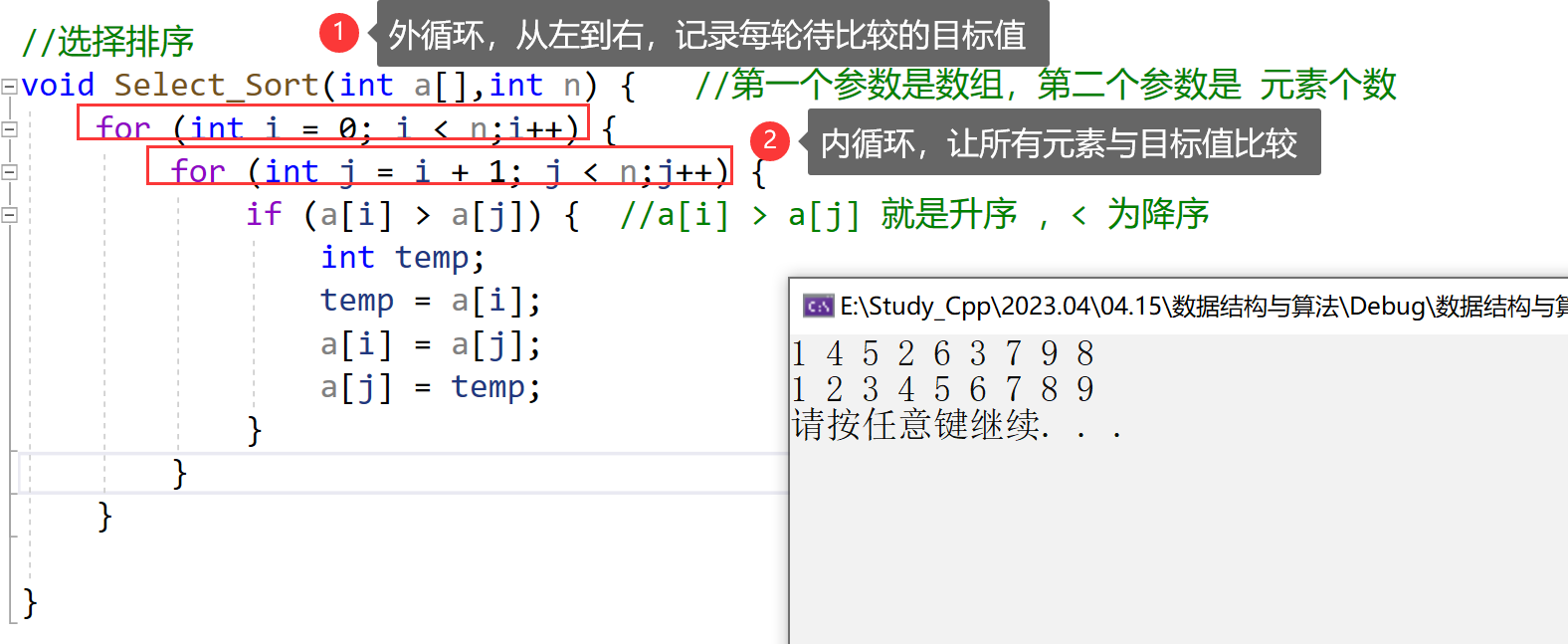
1.3、算法实现
//选择排序
void Select_Sort(int a[],int n) { //第一个参数是数组,第二个参数是 元素个数
for (int i = 0; i < n;i++) {
for (int j = i + 1; j < n;j++) {
if (a[i] > a[j]) { //a[i] > a[j] 就是升序 ,< 为降序
int temp;
temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
}
}
1.4、算法分析
1、时间复杂度:O(n2)
2、空间复杂度:O(1)
3、会改变数据排列顺序,是不稳定排序
4、适用于数据量小,或有部分数据已经排序的情况
2、 冒泡排序
2.1、算法思想
1、比较相邻的元素,如果前一个元素比后一个元素大,就交换两个元素的位置。
2、对每一对相邻元素作相同的工作,从开第一对元素到结尾最后一对元素,最终最后位置的元素就是最大值。
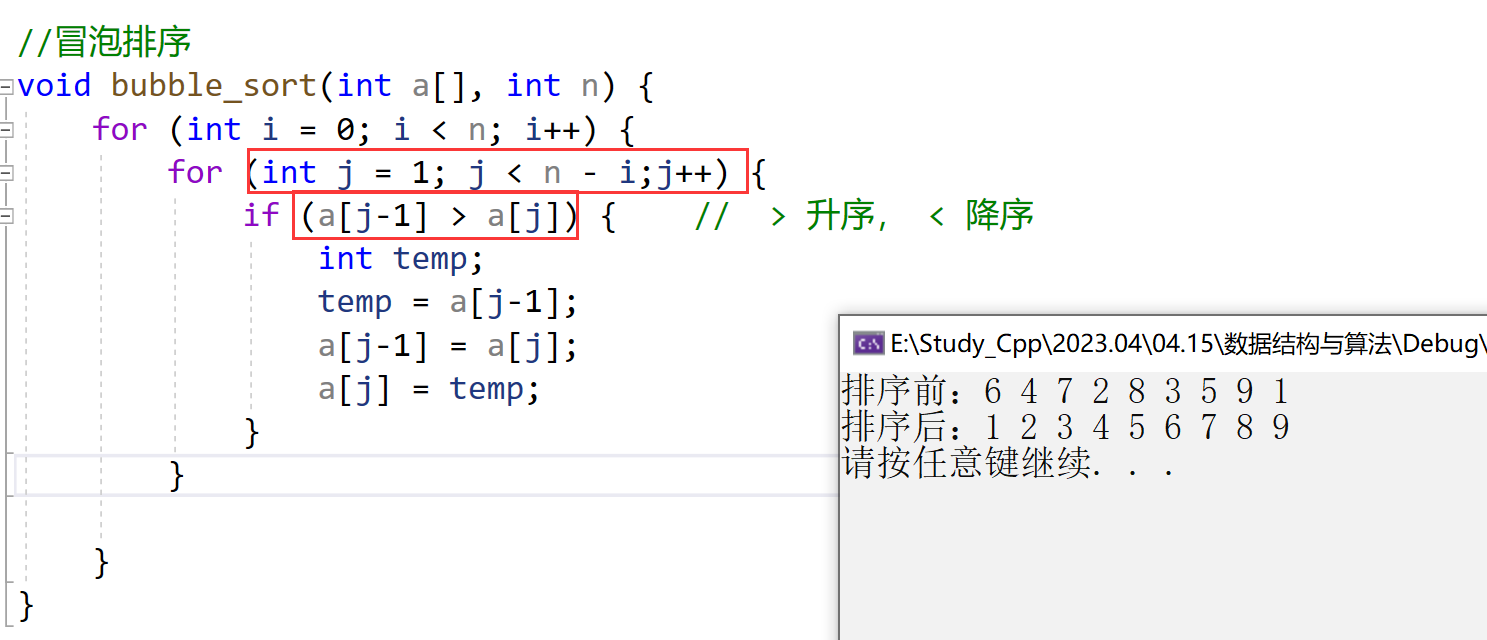
2.2、算法实现
//冒泡排序
void bubble_sort(int a[], int n) {
for (int i = 0; i < n; i++) {
for (int j = 1; j < n - i;j++) {
if (a[j-1] > a[j]) { // > 升序, < 降序
int temp;
temp = a[j-1];
a[j-1] = a[j];
a[j] = temp;
}
}
}
}
2.3、算法分析
1、时间复杂度:O(n2)
2、冒泡在比较两个相邻元素后,再决定是否互换位置,不会改变原来排列的顺序,因此是稳定排序算法。
3、空间复杂度:O(1)
4、冒泡排序法适合数据量小,或有部分数据已经排过序的情况。
2.4、改进冒泡排序
缺点:无论数据是否已排序完成都固定会执行n(n-1)/2次数据比较。
改进方法:加入一个判断条件来判断何时可以提前结束循环。
//改进冒泡排序
void bubble_sort1(int a[], int n) {
for (int i = 0; i < n; i++) {
/*
引入一个标志,如果为0 则说明以下未发生交换,
即,后面的数据已经有序。
如果不等于 0 ,说明后面暂时无序,还需要比较
*/
int flag = 0;
for (int j = 1; j < n - i; j++) {
if (a[j - 1] > a[j]) { // > 升序, < 降序
int temp;
temp = a[j - 1];
a[j - 1] = a[j];
a[j] = temp;
flag++;
}
}
if (flag == 0) { /为 0 ,结束排序
break;
}
}
}
3、插入排序
3.1、算法思想
1、把所有的元素分为两组,已经排序的和未排序的
2、找到未排序的组中的第一个元素,向已排序的组中进行插入;
3、倒序遍历已排序的元素,依次和待插入的元素进行比较,如果某个元素小于待插入元素,则交换两者位置。
3.2、算法实现
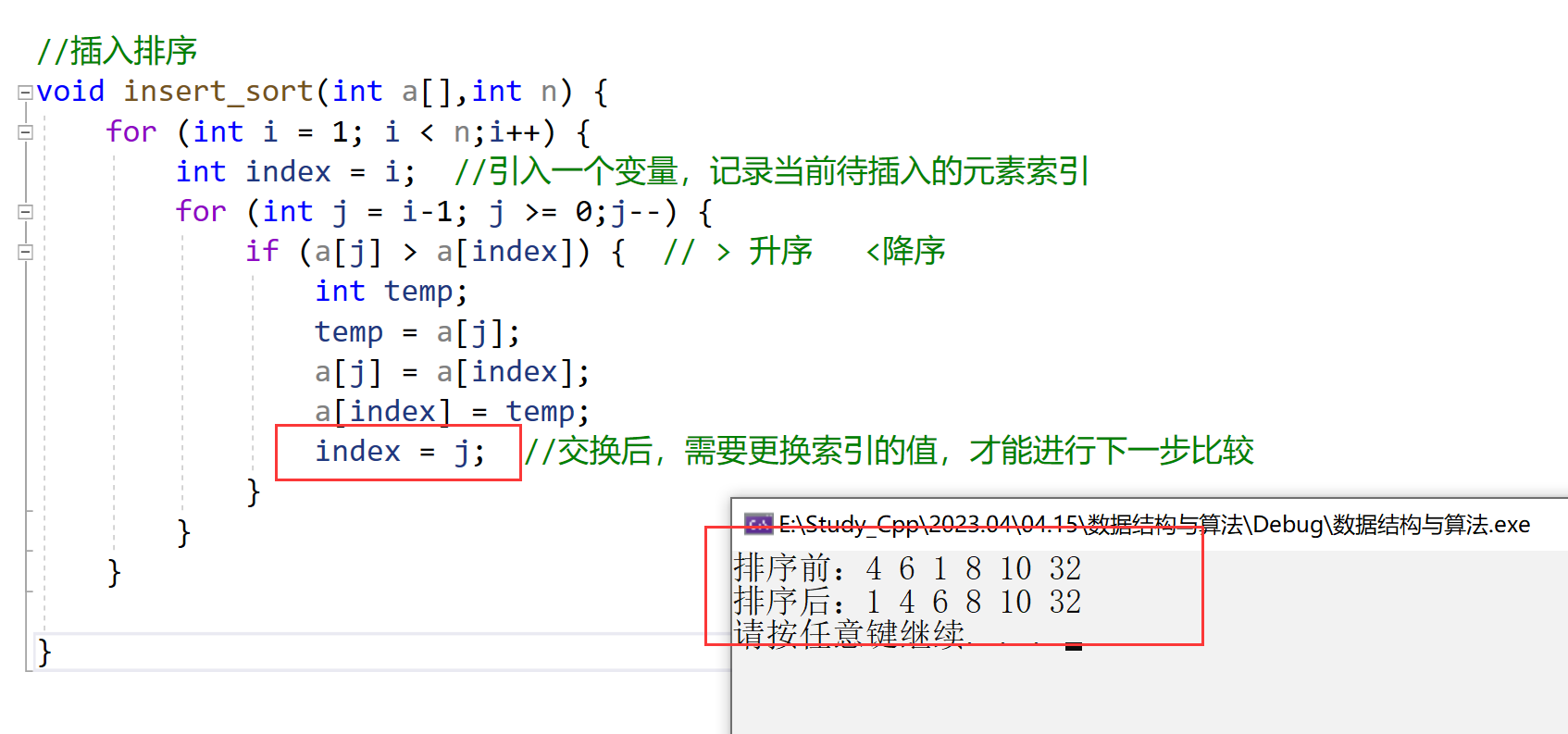
//插入排序
void insert_sort(int a[],int n) {
for (int i = 1; i < n;i++) {
int index = i; //引入一个变量,记录当前待插入的元素索引
for (int j = i-1; j >= 0;j--) {
if (a[j] > a[index]) { // > 升序 <降序
int temp;
temp = a[j];
a[j] = a[index];
a[index] = temp;
index = j; //交换后,需要更换索引的值,才能进行下一步比较
}
}
}
}
3.3、算法分析
1、时间复杂度:O(n^2)
2、插入排序是稳定的排序
3、空间复杂度:O(1)
4、适用于大部分数据已经排序的情况,或者往已排序的数据库中添加新的元素,然后再次排序的情况。
5、插入排序会造成大量的数据迁移,建议在链表上使用。
4、希尔排序
4.1、算法思想
1、选定一个增长量h,按照增长量h作为数据分组的一句,对数据进行分组。
2、对分好组的每一组数据进行插入排序。
3、减小增长量,最小减为1,重复第二步操作。
4.2、增长量选定规则
对于初始增长量,没有固定的规则,很多论文研究了各种不同的递增序列,但都无法增量那个序列是最好的,这里简单介绍两种:
1、
int h = 1;
while(h < 数组长度 / 2){
h = 2*h -1;
}2、 h = 数组长度 / 2;
每次减少量: h = h /2;
4.3、算法实现
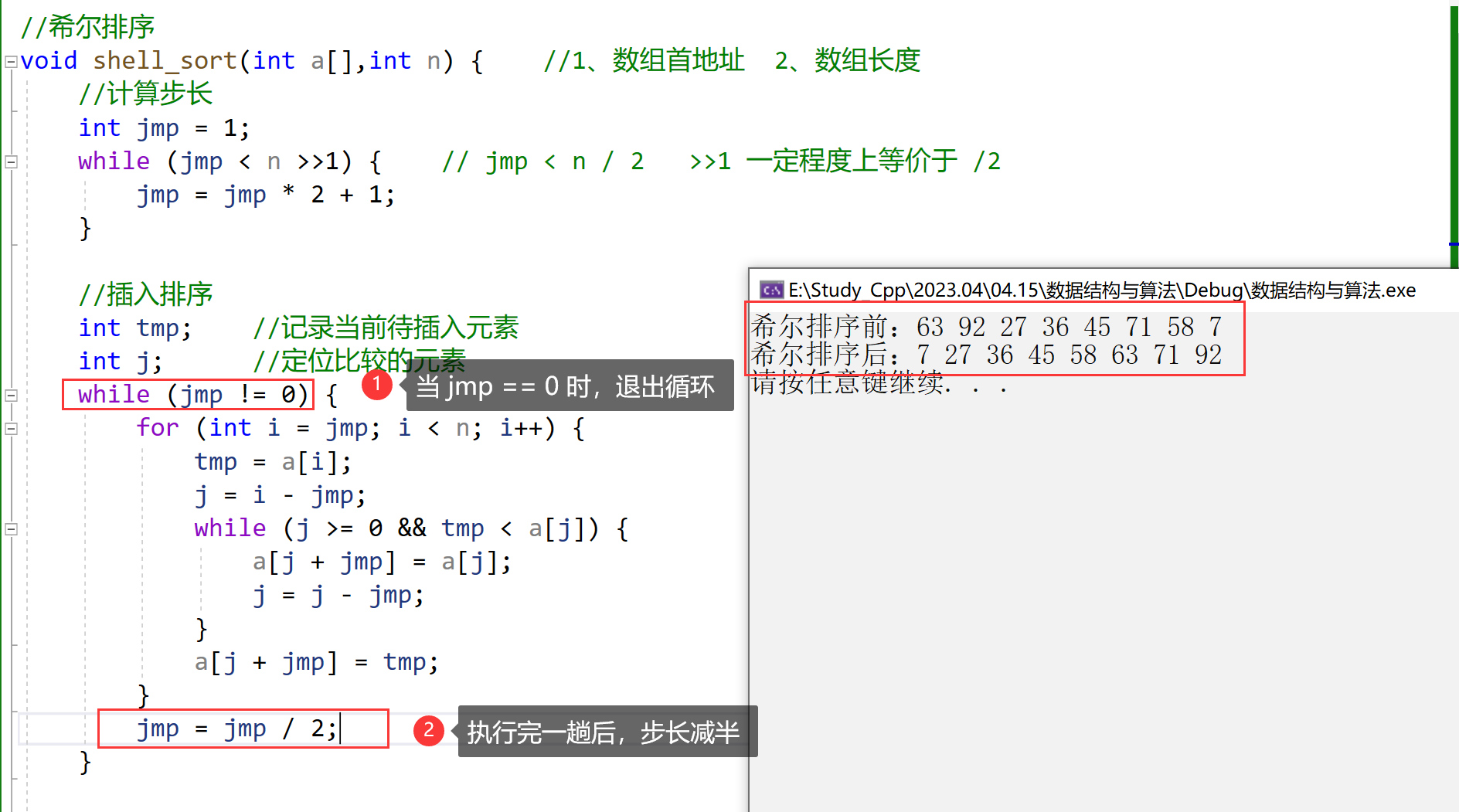
//希尔排序
void shell_sort(int a[],int n) { //1、数组首地址 2、数组长度
//计算步长
int jmp = 1;
while (jmp < n >>1) { // jmp < n / 2 >>1 一定程度上等价于 /2
jmp = jmp * 2 + 1;
}
//插入排序
int tmp; //记录当前待插入元素
int j; //定位比较的元素
while (jmp != 0) {
for (int i = jmp; i < n; i++) {
tmp = a[i];
j = i - jmp;
while (j >= 0 && tmp < a[j]) {
a[j + jmp] = a[j];
j = j - jmp;
}
a[j + jmp] = tmp;
}
jmp = jmp / 2;
}
}
4.4、算法分析
1、当初始步长 h = 数组长度 / 2 时 ,时间复杂度为O(n3/2)
2、稳定的排序算法
3、空间复杂度:O(1)
4、适用于大部分数据已经排序的情况
5、归并排序
5.1、算法思想
1、尽可能的将一组数据才分成两个等分的子组,并对每个子组进行拆分,直到每个子组的元素个数为1为止
2、将相邻的两个子组进行合并成一个有序的大组
3、重复步骤2,直到最终只有一个组为止。
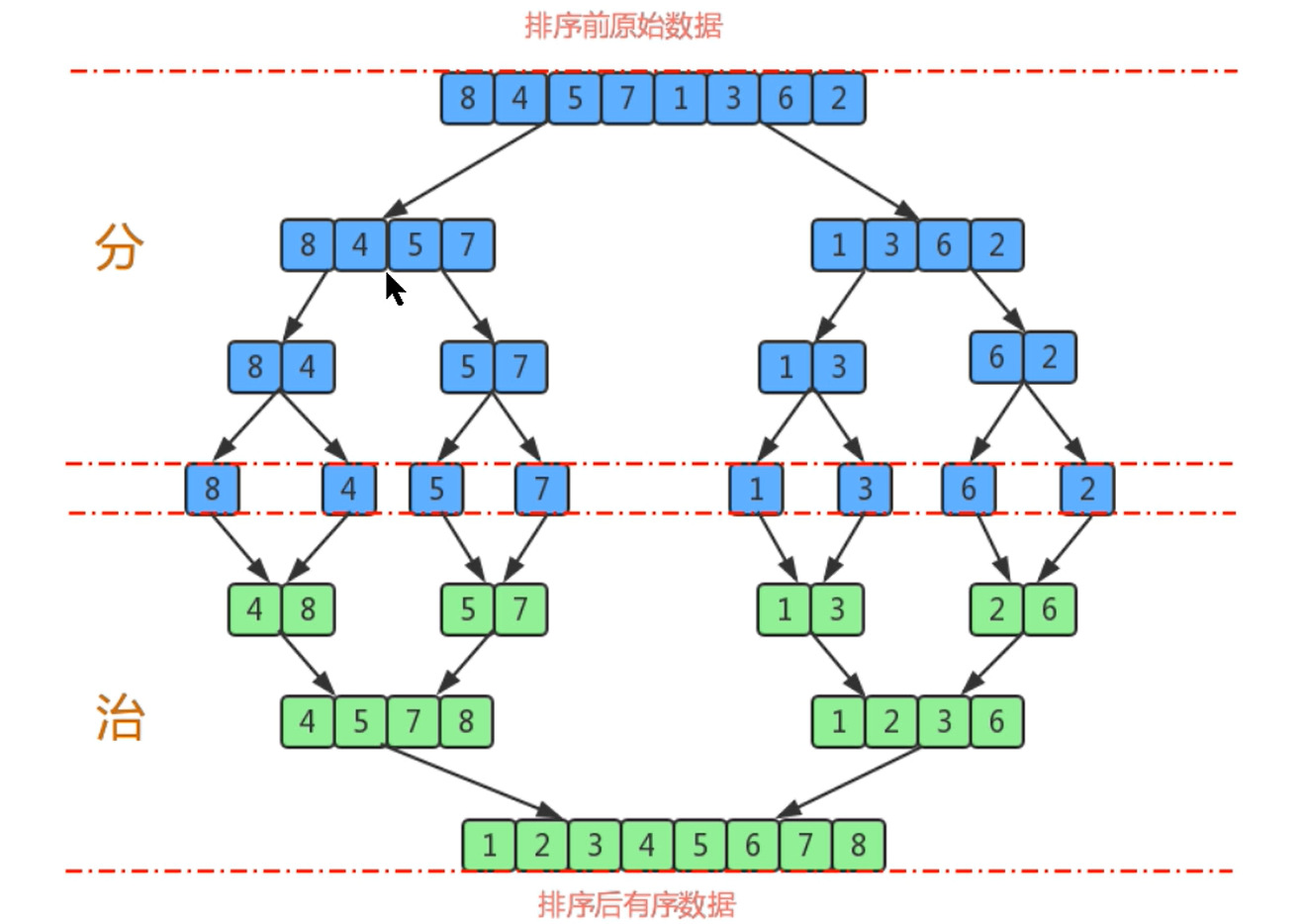
5.2、算法实现
//归并排序
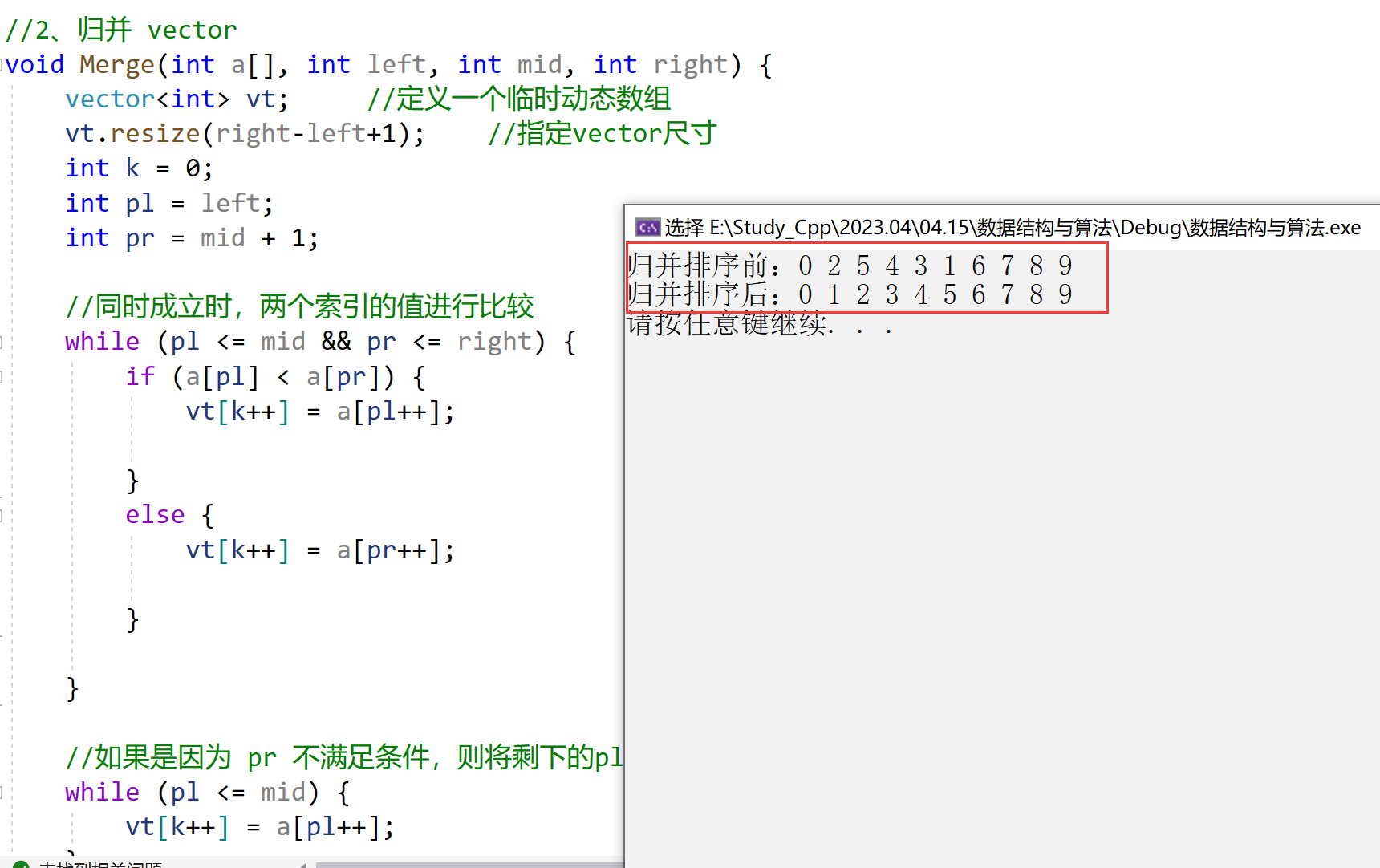
//2、归并 vector
void Merge(int a[], int left, int mid, int right) {
vector<int> vt; //定义一个临时动态数组
vt.resize(right-left+1); //指定vector尺寸
int k = 0;
int pl = left;
int pr = mid + 1;
//同时成立时,两个索引的值进行比较
while (pl <= mid && pr <= right) {
if (a[pl] < a[pr]) {
vt[k++] = a[pl++];
}
else {
vt[k++] = a[pr++];
}
}
//如果是因为 pr 不满足条件,则将剩下的pl索引元素放入
while (pl <= mid) {
vt[k++] = a[pl++];
}
//如果是因为 pl 不满足条件,则将剩下的pr索引元素放入
while (pr <= right) {
vt[k++] = a[pr++];
}
//拷贝 临时 -> 目标
for (int i = left, j = 0; i <= right; i++, j++) {
a[i] = vt[j];
}
}
//1、排序
void Merge_sort(int a[],int left,int right) { //1、数组首地址,2、组的左边界,3、组的右边界
//递归到子组只有一个元素时,退出
if (left == right) {
return;
}
//折半,划分子组
int mid = (left + right) / 2;
//左子组归并排序
Merge_sort(a,left,mid);
//右子组归并排序
Merge_sort(a, mid+1,right);
//排序后,进行归并
Merge(a,left,mid,right);
}
5.3、算法分析
1、时间复杂度:O(nlog2n)
2、缺点:需要申请数组空间,导致空间浪费,是典型的空间换时间操作
3、归并排序是稳定排序法
6、快速排序
6.1、算法思想
1、在数据中找一个虚拟的中间件(一般就是第一个元素)
2、按照中间值,将小于中间值的数据放在中间值的左边,大于中间值的数据放在右边
3、再以同样的方式分别处理左右两边的数据,直到排完序为止。
6.2、算法实现
1、递归
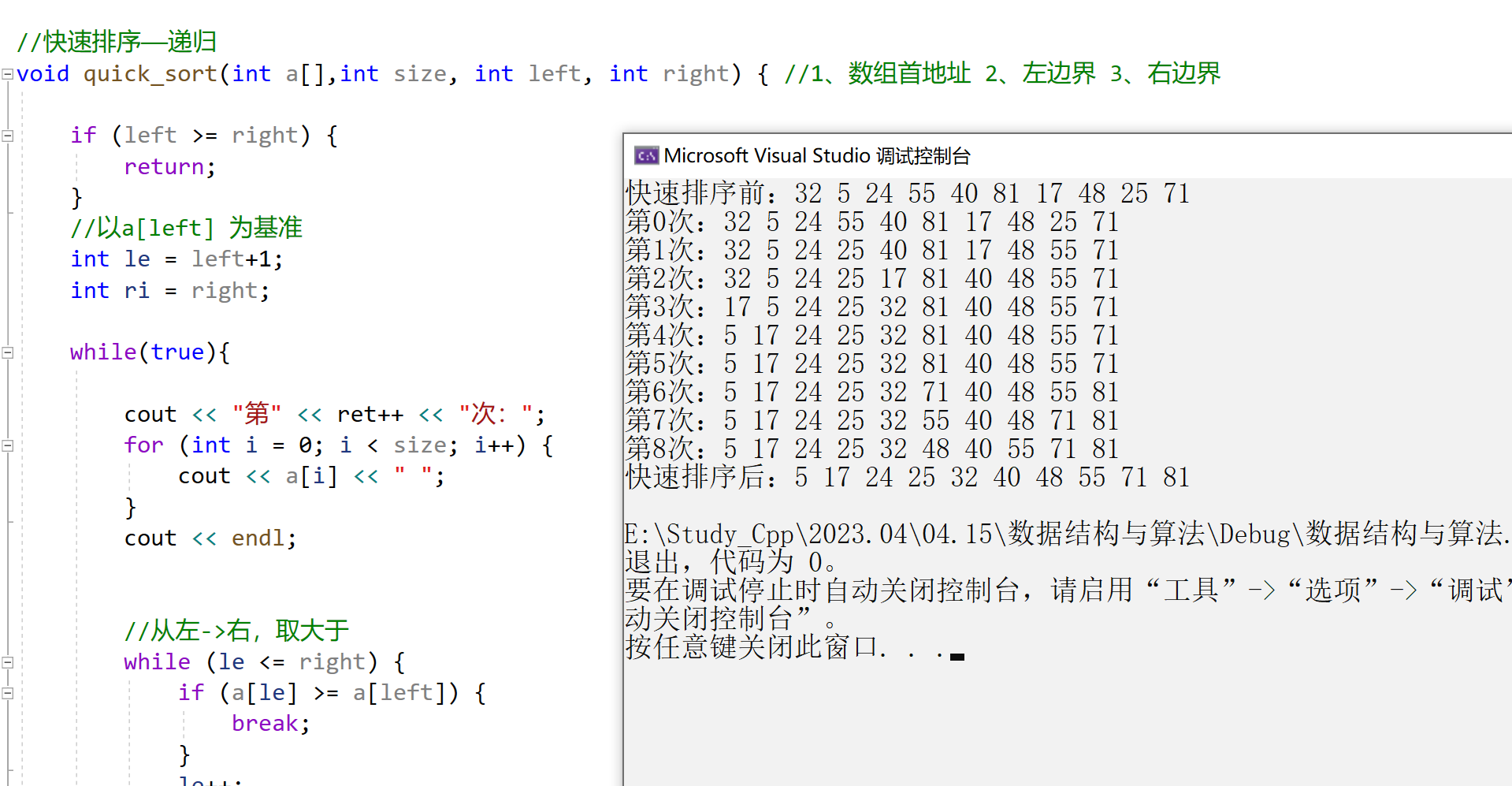
//快速排序——递归
void quick_sort(int a[],int size, int left, int right) { //1、数组首地址 2、左边界 3、右边界
if (left >= right) {
return;
}
//以a[left] 为基准
int le = left+1;
int ri = right;
while(true){
cout << "第" << ret++ << "次:";
for (int i = 0; i < size; i++) {
cout << a[i] << " ";
}
cout << endl;
//从左->右,取大于
while (le <= right) {
if (a[le] >= a[left]) {
break;
}
le++;
}
//从右->左,取小于
while (ri >= left+1) {
if (a[ri] <= a[left]) {
break;
}
ri--;
}
//如果 左边索引 < 右边索引 ,交换le 和 ri索引的值
if (le < ri) {
int temp1;
temp1 = a[le];
a[le] = a[ri];
a[ri] = temp1;
}
else {
break;
}
}
//当左边索引 >= 右边索引 ,将ri位置的元素和base 交换
if (le >= ri) {
int temp;
temp = a[left];
a[left] = a[ri];
a[ri] = temp;
quick_sort(a,size,left,ri-1);
quick_sort(a,size,ri+1,right);
}
}
2、非递归—利用栈,代替递归
// 子组排序算法
int get_key(int a[],int left, int right) {
//取基准为 a[left]
int lf1 = left+1;
int rg1 = right;
while (true) { //控制比较躺数
//左 -> 右
while (lf1 <= right) {
if (a[lf1] > a[left]) {
break;
}
lf1++;
}
//右 -> 左
while (rg1 >= left + 1) {
if (a[rg1] < a[left]) {
break;
}
rg1--;
}
if (lf1 < rg1) {
int temp = a[lf1];
a[lf1] = a[rg1];
a[rg1] = temp;
}
else {
break;
}
}
if (lf1 >= rg1) {
int tmp = a[left];
a[left] = a[rg1];
a[rg1] = tmp;
}
return rg1;
}
//快速排序——非递归 栈
void quick_sort_no(int a[],int size, int left, int right) {
if (left>=right) {
return;
}
stack<int> s;
s.push(left);
s.push(right);
while (!s.empty()) {
int rg = s.top();
s.pop();
int lf = s.top();
s.pop();
int key = get_key(a,lf, rg);
cout << "第" << ret++ << "次:";
for (int i = 0; i < size; i++) {
cout << a[i] << " ";
}
cout << endl;
if (key-1 > lf ) {
s.push(lf);
s.push(key-1);
}
if (key+1 < rg) {
s.push(key+1);
s.push(rg);
}
}
}
3、非递归—利用队列,代替递归
// 子组排序算法
int get_key(int a[],int left, int right) {
//取基准为 a[left]
int lf1 = left+1;
int rg1 = right;
while (true) { //控制比较躺数
//左 -> 右
while (lf1 <= right) {
if (a[lf1] > a[left]) {
break;
}
lf1++;
}
//右 -> 左
while (rg1 >= left + 1) {
if (a[rg1] < a[left]) {
break;
}
rg1--;
}
if (lf1 < rg1) {
int temp = a[lf1];
a[lf1] = a[rg1];
a[rg1] = temp;
}
else {
break;
}
}
if (lf1 >= rg1) {
int tmp = a[left];
a[left] = a[rg1];
a[rg1] = tmp;
}
return rg1;
}
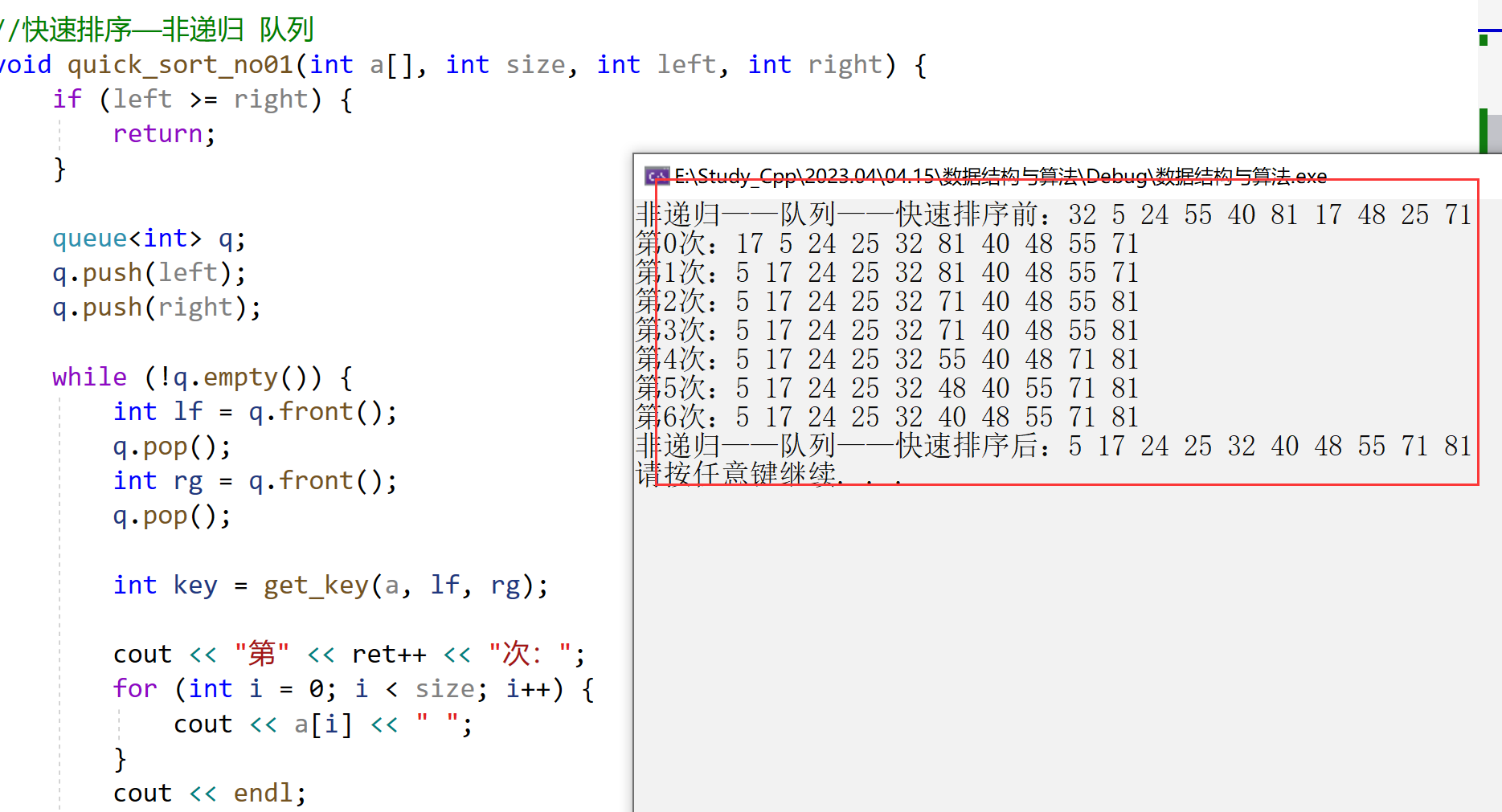
//快速排序——非递归 队列
void quick_sort_no01(int a[], int size, int left, int right) {
if (left >= right) {
return;
}
queue<int> q;
q.push(left);
q.push(right);
while (!q.empty()) {
int lf = q.front();
q.pop();
int rg = q.front();
q.pop();
int key = get_key(a, lf, rg);
cout << "第" << ret++ << "次:";
for (int i = 0; i < size; i++) {
cout << a[i] << " ";
}
cout << endl;
if (key - 1 > lf) {
q.push(lf);
q.push(key - 1);
}
if (key + 1 < rg) {
q.push(key + 1);
q.push(rg);
}
}
}
6.3、算法分析
1、最好和平均情况下,时间复杂度O(nlog2n),最坏,O(n^2)
2、快速排序不是稳定的排序算法
3、最好情况下,空间复杂度O(log2n),最坏情况下,O(n)
4、快速排序算法是平均速度最快的算法。
7、基数排序(桶排序)
7.1、算法思想
从数据的低位(LSD)或者高位 (MSD) 开始,按照这一位数字的值(0~9)放到对应的编号为 0~9 的桶中。我们按照这一位数字进行完了排序,再按照次低位(下一位)数字进行上述的操作。重复这样的操作一直到最高位,直到最后每一位数字都进行完排序,整个基数排序完成。
7.2、算法步骤
1、建立一个桶,存放每个位数上出现元素的个数
2、最低位开始,将数列按照该位的数值放入到桶中,
3、将桶中的存放的数据按 a[i+1] = a[i],依次相加,计算出当前数字的位置。
4、把数列按照在当前桶中的顺序依次存放到临时数组中
5、将临时数组的值,拷贝到原数组中
6、依次循环,直到最高位比较结束,排序完成。
7.3、算法实现
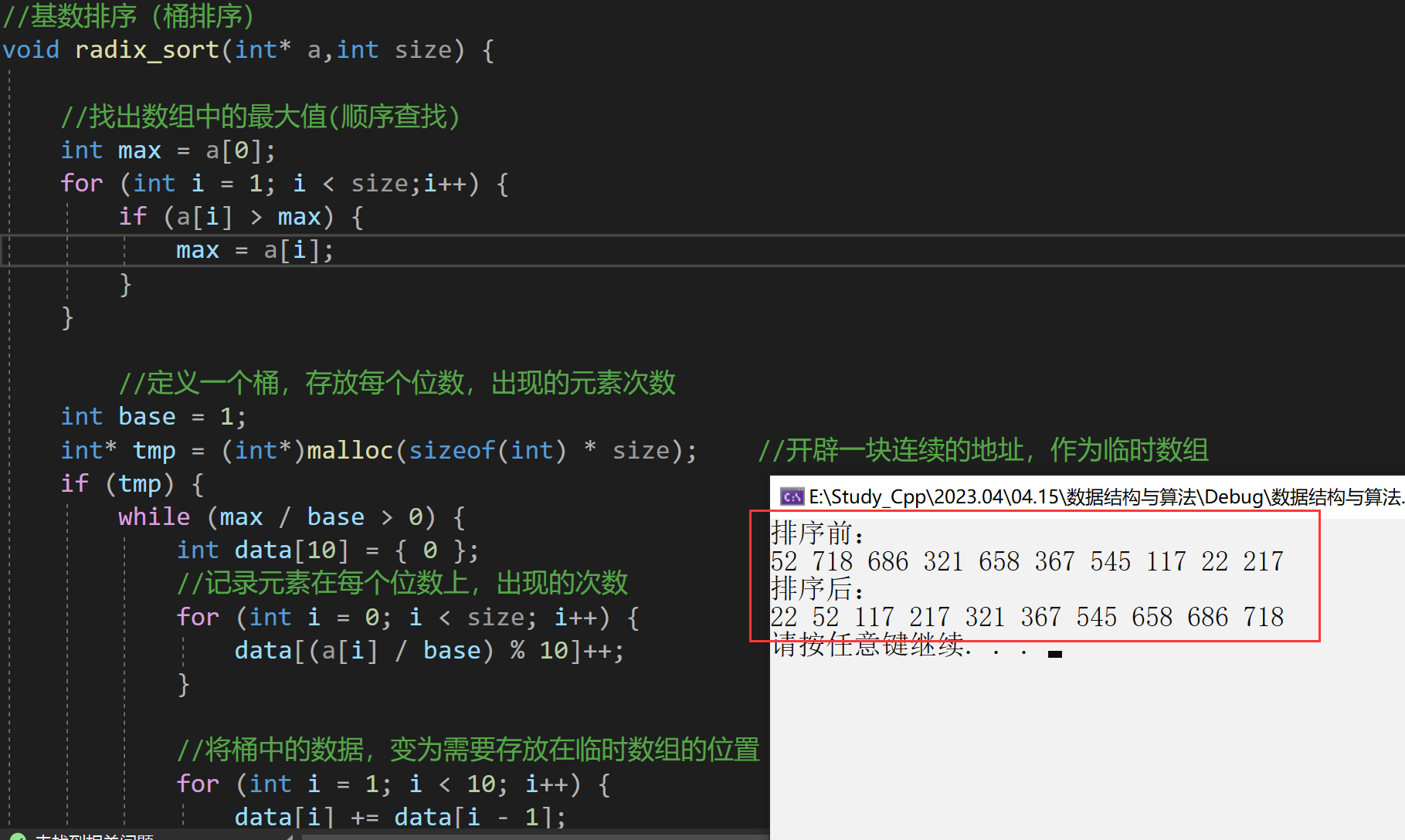
//基数排序(桶排序)
void radix_sort(int* a,int size) {
//找出数组中的最大值(顺序查找)
int max = a[0];
for (int i = 1; i < size;i++) {
if (a[i] > max) {
max = a[i];
}
}
//定义一个桶,存放每个位数,出现的元素次数
int base = 1;
int* tmp = (int*)malloc(sizeof(int) * size); //开辟一块连续的地址,作为临时数组
if (tmp) {
while (max / base > 0) {
int data[10] = { 0 };
//记录元素在每个位数上,出现的次数
for (int i = 0; i < size; i++) {
data[(a[i] / base) % 10]++;
}
//将桶中的数据,变为需要存放在临时数组的位置
for (int i = 1; i < 10; i++) {
data[i] += data[i - 1];
}
for (int i = size - 1; i >= 0; i--) {
tmp[data[(a[i] / base) % 10] - 1] = a[i];
data[(a[i] / base) % 10]--;
}
for (int i = 0; i < size; i++) {
a[i] = tmp[i];
}
base = base * 10;
}
}
free(tmp);
}
7.4、算法分析
1、时间复杂度:O(nlogpk)
2、基数排序是稳定排序法
3、空间复杂度:O(n*p),n是原始数据个数,p是数据字符数
4、如果n很大,p固定或者很小,此排序效率很高。