随机网络构建
文章目录
- 随机网络构建
- @[toc]
- 1 随机网络定义
- 2 网络拓扑性质
- 2.1 边数分布
- 2.2 度分布
- 3 代码实现
文章目录
- 随机网络构建
- @[toc]
- 1 随机网络定义
- 2 网络拓扑性质
- 2.1 边数分布
- 2.2 度分布
- 3 代码实现
1 随机网络定义
随机网络与规则网络相对应,最为经典的随机网络模型是Erdös和Rényi研究的ER随机图模型,ER随机图模型有两种定义方式:
- 方式一:给定节点数 N N N,固定连边数 M M M。每次随机选择一对节点并连边,重复 M M M次。每次选择两个不同节点并且没有连接的节点对,记作 G ( N , M ) G(N,M) G(N,M)。算法如下:
首先给定 N N N个节点和 M M M条待连接边
- 随机选取一对没有边相连的不同节点,并在这对节点添加一条连边
- 重复上述步骤 M M M次
- 方式二:给定 N N N个节点,任意两个不同节点之间有一条连边概率固定为 p p p,记作 G ( N , p ) G(N,p) G(N,p),算法如下
初始化 N N N个节点和固定概率 p p p,
- 选择一对没有边相连的节点对
- 生成一个随机数 r ∈ [ 0 , 1 ] r\in[0,1] r∈[0,1]
- 若r<p,则在这两个节点之间添加一条边;否则不添加
- 重复上述步骤直至所有节点都被考虑一次。
特殊地,当 p = 0 p=0 p=0,则形成 N N N个孤立的节点; p = 1 p=1 p=1,则形成 N N N阶全局耦合网络,对于无向网络,连边数为 N ( N − 1 ) / 2 N(N-1)/2 N(N−1)/2;当 p ∈ ( 0 , 1 ) p\in(0,1) p∈(0,1),连边数取值位于区间 ( 0 , N ( N − 1 ) / 2 ) (0,N(N-1)/2) (0,N(N−1)/2)
2 网络拓扑性质
2.1 边数分布
给定随机网络
G
(
N
,
p
)
G(N,p)
G(N,p),该网络刚好有
M
M
M条边的概率:
P
(
M
)
=
C
C
N
2
M
p
M
(
1
−
p
)
C
N
2
−
M
P(M) = C_{C_N^2}^M p^M(1-p)^{C_N^2-M}
P(M)=CCN2MpM(1−p)CN2−M
C
N
2
C_N^2
CN2表示随即网络理论最大边数,刚好有
M
M
M条连边的概率满足二项分布。根据二项分布性质,随机变量
M
M
M的期望
E
(
M
)
=
∑
M
=
0
C
N
2
M
P
(
M
)
=
p
N
(
N
−
1
)
/
2
E(M) = \sum_{M=0}^{C_N^2}MP(M) = pN(N-1)/2
E(M)=M=0∑CN2MP(M)=pN(N−1)/2
上述结果是显然的,因为一对节点存在连边概率为
p
p
p,理论上存在
N
(
N
−
1
)
/
2
N(N-1)/2
N(N−1)/2条连边,因此理论上仅存在
E
(
M
)
E(M)
E(M)条连边。根据二项分布的二阶矩公式,不难得到随机变量
M
M
M方差为
D
(
M
)
=
p
(
1
−
p
)
N
(
N
−
1
)
2
D(M) = p(1-p)\dfrac{N(N-1)}{2}
D(M)=p(1−p)2N(N−1)
2.2 度分布
任意节点与其他
k
k
k个节点相连接的概率为
p
k
(
1
−
p
)
N
−
1
−
k
p^k(1-p)^{N-1-k}
pk(1−p)N−1−k,这里
p
p
p为连接概率,与
k
k
k个节点连接,但与其他
N
−
1
−
k
N-1-k
N−1−k(除去自身)个节点不相连。选择方式共有
C
N
−
1
k
C_{N-1}^k
CN−1k种,则
P
(
k
)
=
C
N
−
1
k
p
k
(
1
−
p
)
N
−
1
−
k
P(k) =C_{N-1}^kp^k(1-p)^{N-1-k}
P(k)=CN−1kpk(1−p)N−1−k
根据二项分布期望公式得到
E
(
k
)
=
p
(
N
−
1
)
,
D
(
k
)
=
p
(
1
−
p
)
(
N
−
1
)
E(k) = p(N-1),D(k) =p(1-p)(N-1)
E(k)=p(N−1),D(k)=p(1−p)(N−1)
3 代码实现
下面使用R语言实现随机网络构建。可以快速使用igraph包,调用函数erdos.renyi.game即可。
library(igraph)
# ER网络构造
g.er <- erdos.renyi.game(10, 0.5)
ecount(g.er)
0.5*10*9/2
plot(g.er)

也可以自己构建随机网络函数,参照第二种定义方式 G ( N , p ) G(N,p) G(N,p)的算法
ER <- function(N, p) {
if (class(N) != "numeric") stop("节点数必须是整数")
# N:节点个数
# p: 连接概率
library(igraph)
M <- matrix(0, nrow = N, ncol = N)
W <- matrix(0, nrow = N, ncol = N)
for (i in 1:(N-1)) {
for (j in (i+1):N) {
if (j != i) {
if (runif(1) < p) W[i, j] <- 1
}
}
}
g <- graph_from_adjacency_matrix(W, mode = "upper")
list(matrix = W, Graph = g)
}
M <- 50
p <- 0.1
g <- ER(N = M, p=p)
plot(g$Graph,layout = layout.circle)
# 实际值变数
ecount(g$Graph)
# 理论值变数
p * M * (M - 1) / 2

上面的随机网络是无向的,根据第二种定义也可以扩充为有向随机网络
ER <- function(n, probability,type = "undirected") {
# N:节点个数
# p: 连接概率
# type网络类型
if (class(n) != "numeric") stop("节点数必须是整数")
if (probability < 0 | probability > 1) stop("连接概率取值为0-1")
library(igraph)
M <- matrix(0, nrow = n, ncol = n)
W <- matrix(0, nrow = n, ncol = n)
switch (type,
"undirected" = {
for (i in 1:(n-1)) {
for (j in (i+1):n) {
if (j != i) {
if (runif(1) < probability) W[i, j] <- 1
}
}
}
g <- graph_from_adjacency_matrix(W, mode = "upper")
},
"directed" = {
for (i in 1:n) {
for (j in 1:n) {
if (j != i) {
if (runif(1) < probability) W[i, j] <- 1
}
}
}
g <- graph_from_adjacency_matrix(W, mode = "directed")
}
)
list(matrix = W, Graph = g)
}
M <- 50
p <- 0.2
number_edges =numeric()
number_sampling = 1000
for(i in 1:number_sampling){
g <- ER(n = M, probability=p,type = "undirected")
number_edges[i] <- ecount(g$Graph)
}
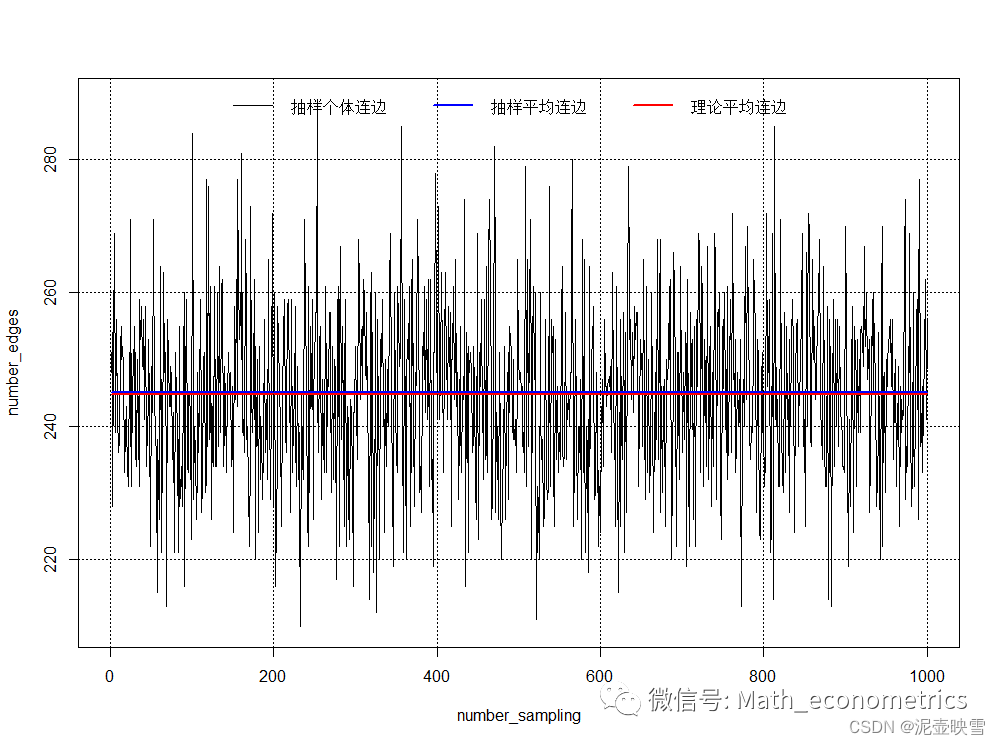
plot(1:number_sampling,number_edges,type = "l",xlab = "number_sampling",ylab = "number_edges")
lines(1:number_sampling, rep(p * M * (M - 1)/2,number_sampling),col = "blue",lwd = "2")
lines(1:number_sampling, rep(mean(number_edges),number_sampling),col = "red",lwd = "2")
grid(col = "black")
legend("top",legend = c("抽样个体连边","抽样平均连边","理论平均连边"),
col = c("black","blue","red"),lwd = c(1,2,2),
bty = "n", ncol = 3,cex = 1,text.width = 150)
var(number_edges)
p*(1-p)*M*(M-1)/2
参考书籍:汪小帆等,网络科学导论[M]. 北京: 高等教育出版社, 2012.