GMesh网格介绍

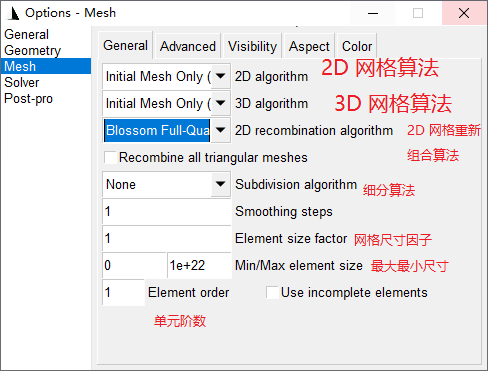
2D mesh algorithm

1. MeshAdapt：这是一种自适应网格算法，可在需要更大的精度或在某些区域需要更密集的网格时自动添加额外的网格。该算法的优点包括较高的收敛性和灵活性，它可以让用户在需要的地方添加更多的网格，但同时也可能会引入更多的节点和元素，从而增加计算时间和内存占用。
2. Automatic：这是一种基于Delaunay三角化的自动网格算法，它具有较好的网格质量和较低的内存占用。由于该算法的计算效率较高，因此在大型计算中使用较为常见。
3. Initial mesh only：这个算法只生成初始网格，而不进行任何形状调整或细化。它适用于需要手动调整和优化网格的情况，在这种情况下，用户通常需要对网格进行手动操作或使用其他网格算法，例如BAMG。
4. Delaunay：这是一种基于Delaunay三角化的算法，它可以生成高质量的网格，并且在网格质量和计算效率之间有很好的平衡。该算法是Gmsh的默认算法，因为它适用于绝大多数的2D几何体。
5. Frontal-Delaunay：这是一种基于前缘三角形算法的曲面网格算法，它可以在处理复杂曲面的情况下生成高质量的网格。该算法的优点是可以处理大多数曲面，但计算效率较低，尤其是当曲面的复杂性增加时。
6. BAMG：这是一种基于梯度的自适应网格算法，可以在局部地区调整网格密度，从而生成高质量的网格。该算法可以更加有效地处理具有变化和复杂度的几何形状，但也需要更多的计算时间和内存。
7. Frontal-Delaunay for Quads：这种算法可以生成质量很高的四边形网格，特别适用于长宽比不同的矩形区域的划分。
8. Packing of Parallelograms：这种算法可以将二维区域划分为平行四边形，生成高品质的四边形网格。
9. Quasi-structured Quad：这种算法是一种准结构化网格算法，可以生成高质量的四边形网格。它适用于要求生成相对结构化的网格的情况。

3D mesh algorithm

1. Delaunay算法：是一种基于Delaunay三角剖分的算法。该算法将每个顶点视为一个Delaunay球，通过计算相邻球之间的共面或共圆关系来构建Delaunay三角形，最终生成网格。该算法一般适用于简单形状的三维几何体和非结构化网格的生成。
2. Initial mesh only算法：该算法仅使用提示网格和大小函数生成网格，可用于快速生成简单形状的网格。
3. Frontal算法：此算法使用一种称为Frontal方法的技术，从一个较粗的生成网格开始，不断切分向内移动直到达到所需的精度。该算法适用于各种类型的三维几何体。
4. MMG3D算法：该算法使用基于前沿移动的方法（Frontal method）和后处理（post-processing）技术来修剪和优化现有的网格以生成更好的网格。算法优化效果较好，但运行速度较慢。
5. R-tree算法：该算法使用空间索引来快速生成网格，将三维空间划分为一系列子区域，然后遍历这些子区域来确定相对于几何体的网格大小和密度。运行速度较快，但是对于不规则形状的几何体可能无法提供好的网格质量。
6. HXT算法：该算法是一种基于Hilbert曲线的算法，将网格点按照Hilbert曲线排序并生成网格，可以有效地减少数据的存储和计算量。

2D recombination algorithm

这些算法可用于优化和重新组合Gmsh中的现有网格，以提高其质量和准确性。

1. 简单重新组合算法：这是一种简单的网格重新组合算法，它以顺序方式搜索所有的网格单元和面，并快速重新组合它们。该算法速度较快，但是产生的网格质量通常不是很好。
2. Blossom重新组合算法：基于匈牙利算法，它通过多次迭代来增加网格点的权值，以便更好地调整四边形的角度、大小和形状。该算法产生的网格质量通常比简单算法更高，但也需要更长的计算时间。
3. 简单全四边形重新组合算法：这种算法与简单重新组合算法类似，但它在重新组合正交四边形时更加有效。该算法速度较快，但是生成的网格可能不是很平滑，需要后处理来进一步优化。
4. Blossom全四边形重新组合算法：这是一种结合了Blossom算法和四边形重构技术的算法，可以更好地处理较大的四边形域，产生更高质量、更平滑的网格。但是，由于算法相对复杂，计算时间较长。

recombine all triangular meshes

用于基于已经存在的三角形网格，重新组合网格单元，生成更高质量、更规则的四边形网格。使用该命令可以有效改善网格质量、减少噪声和变形，并且具有更快的计算速度。具体来说，该命令将重新组合所有存在的三角形网格单元，并从四边形、六边形、八边形等多种类型的组合中选择最优的网格单元。使用该命令需要注意的是，它可能会改变已有的网格结构和拓扑关系，因此建议在对网格进行优化时备份原始网格文件以备不时之需。

smoothing steps

Smoothing Steps是指在进行网格生成或网格优化时，执行平滑算法（Laplace或Jacobi算法）的迭代次数。平滑操作是一种通过通过迭代网格的顶点坐标以使网格网格更加均匀和平滑的算法。为了控制算法的运行和避免无限迭代，Gmsh中提供了可以设置的平滑步骤参数。

平滑步骤数目较少时，可能无法完全平滑网格，导致单元形状不规则或者出现锐角，但可以获得更快的网格生成或优化时间。相反，较多的平滑步骤可以有效平滑网格并减少单元锐角和失真，但需要更长时间才能生成或优化网格。因此，这个参数需要综合考虑网格质量和优化速度，进行最合适的选择。

总之，给定合适的平滑次数，可以使生成的网格更加平稳，单元形状更加规则，从而更好地支持后续物理模拟或仿真的运行。

Use Incomplete Elements

可用于设置是否在生成多边形/多面体网格时使用不完整元素。不完整元素是指在区域和边界之间不匹配的有限元。 在这种情况下，有限元从输入文件的顶部单元格一直绘制到下侧，使用不完整单元。

该选项用于处理以下情况：

1. 区域的边界不是严格对应于输入文件中给出的区域的接口，例如，墙等单元壁并不与边界完全对应。
2. 多边形区域或多面体体积具有使用了不同区域的不同拓扑特征的区域，例如，在该方形的中央存在一个圆形洞，或者在多面体中存在空洞。

使用不完整元素通常会降低有限元网格的质量，但对于一些特定的问题而言，它可以提高计算速度和效率。因此使用或不使用不完整元素需要根据实际情况进行选择。